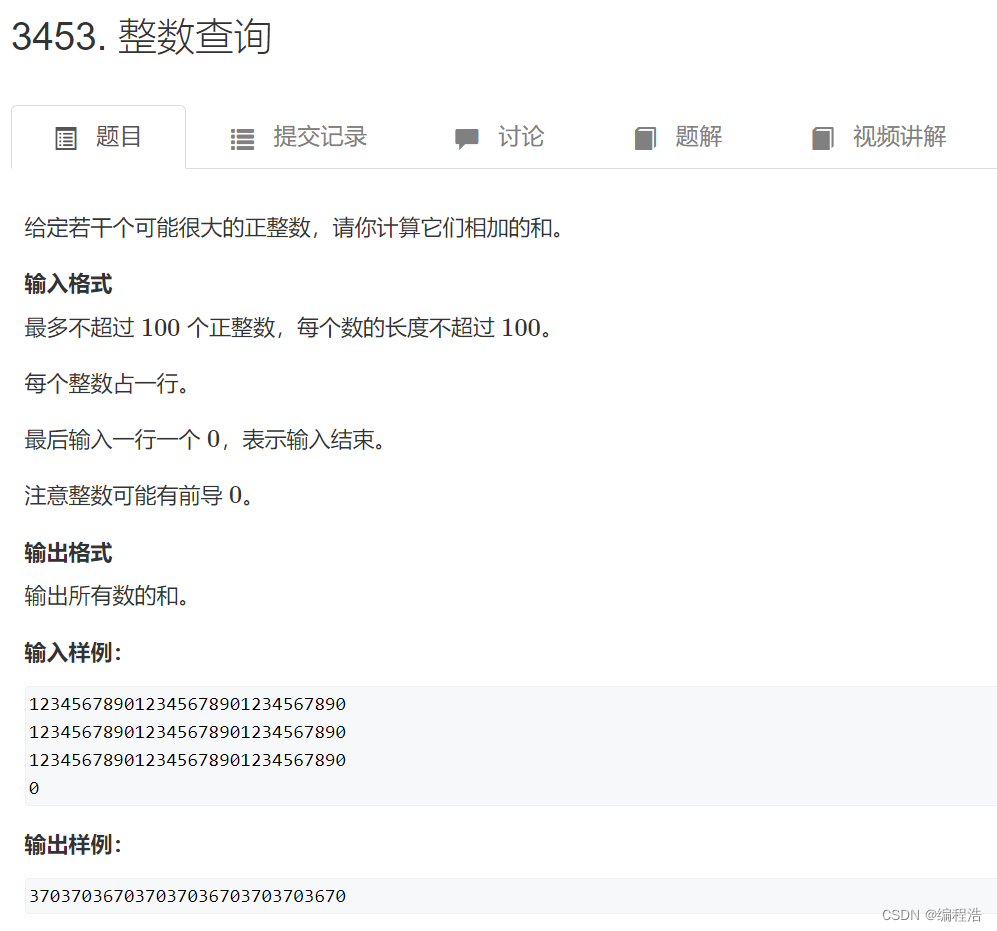
前言

我在刷卡哥的“代码随想录”，自己的总结笔记均会放在“算法刷题-代码随想录”该专栏下。
代码随想录此题链接

思路

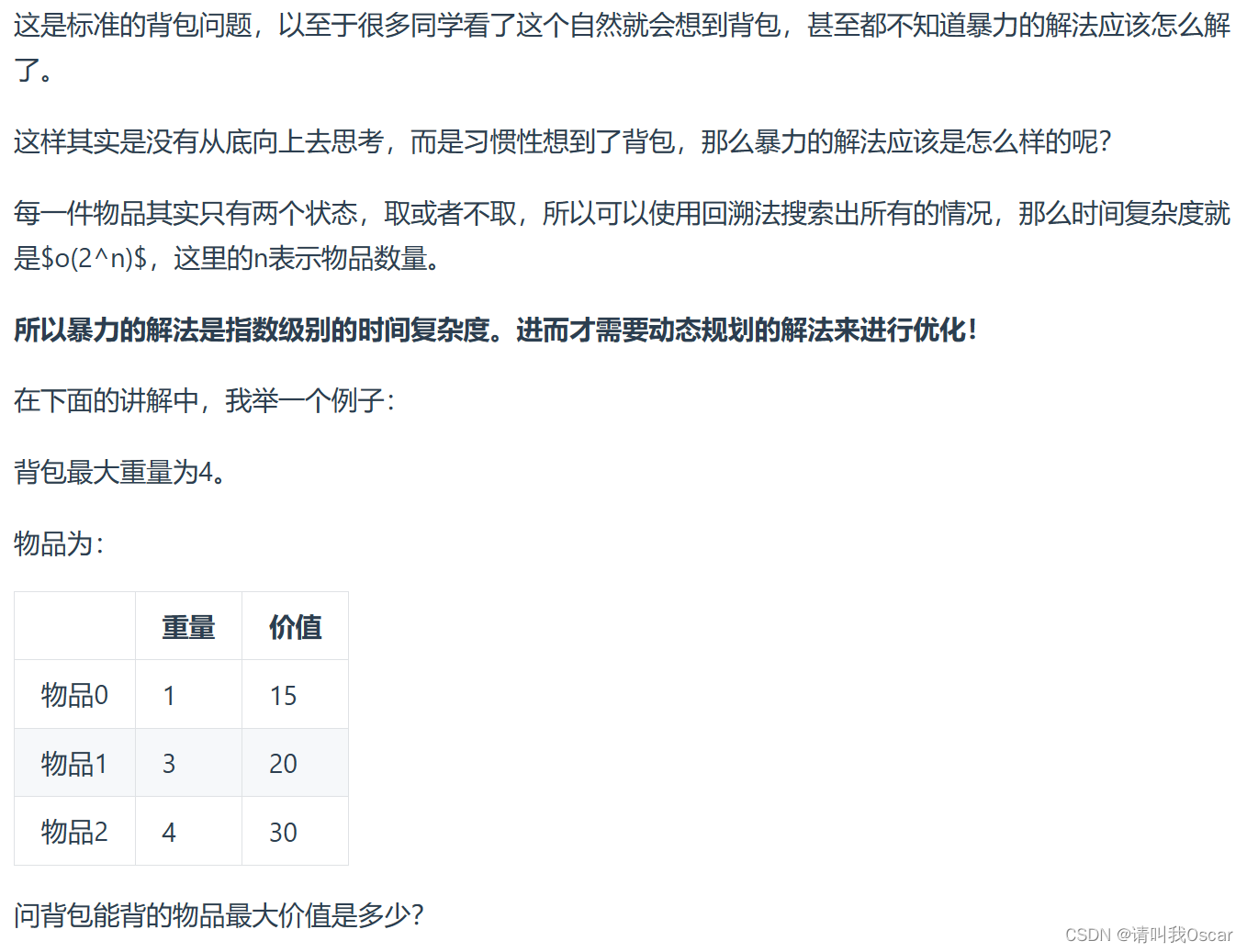
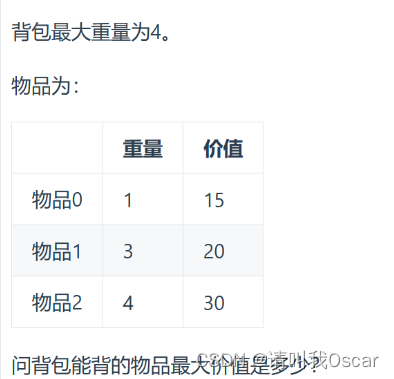
前提，当前的物品有i+1个，编号为0~i，重量weight和价值value数组如下
weight = {1，3，4}
value = {15，20，30}
通过“动态规划五步曲”，

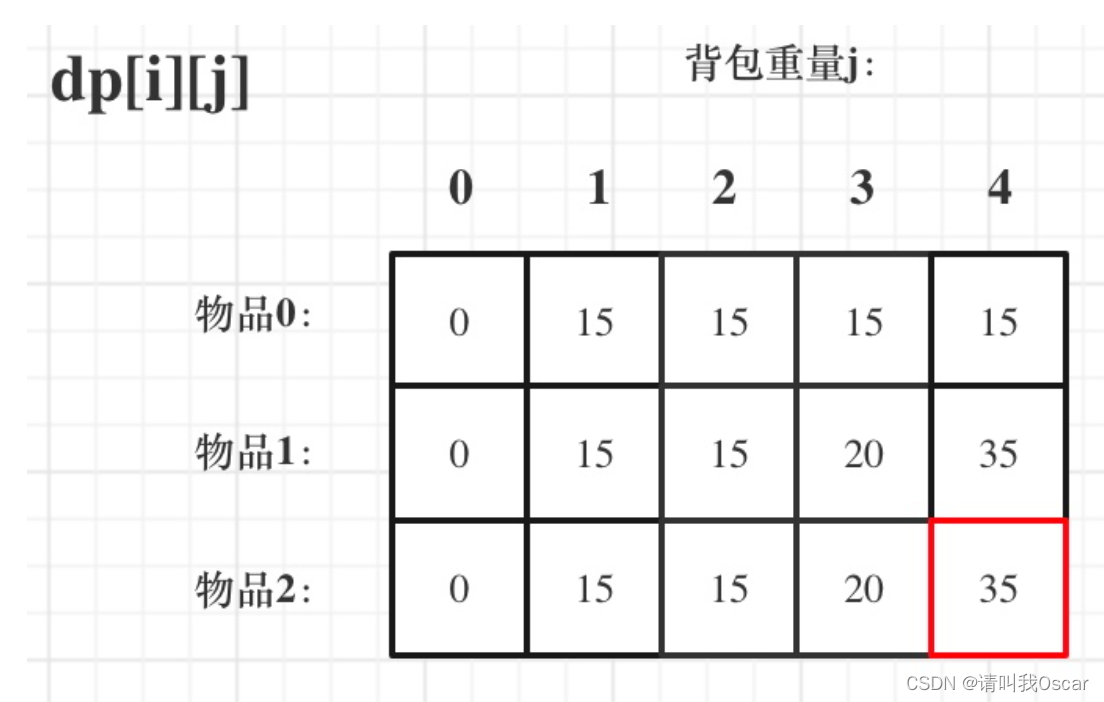
1. 确定dp数组含义：dp[i][j]代表，当前可以获取的物品范围在0~i之间（假设物品编号从0开始），当前背包重量为j，dp[i][j]是这个情况下背包可以装下最大的物品价值。
2. 确定递推公式：
   当前物品大小>背包总容量，dp[i][j]=dp[i - 1][j]
   当前物品大小<=背包总容量，dp[i][j]=max(dp[i - 1][j],dp[i - 1][j - weight[i]] + value[i])
3. 初始化：当前背包的二维数组全部初始化为0，当物品范围为第一个物品时，背包大小大于等于第一个物品的重量时，接下来的全部可以初始化为第一个物品的价值。
4. 遍历方向：
   外层遍历，先遍历物品的序号（从第2个物品开始到最后的物品结束）；
   内层遍历，遍历背包重量（从背包重量为1开始到背包最大重量）；
5. 举例，如题目
   

3. 算法实现

public static void main(String[] args) {
   int[] weight = {1,3,4};
   int[] value = {15,20,30};
   int bagSize = 4;
   testWeightBagProblem(weight,value,bagSize);

}

public static void testWeightBagProblem(int[] weight,int[] value,int bagSize){//bagSize背包总重
    int[][] dp = new int[weight.length][bagSize + 1];//所选物品范围(不包括无物品) 和 包重(从0开始到最大重量)
    //默认dp数组全部初始化0
    for(int i = weight[0];i < bagSize + 1;i++){//初始化，包重大于等于第一个物品时，最大价值为第一个物品的价值
        dp[0][i] = value[0];
    }
    //先固定物品范围  再 固定背包重量
    for(int i = 1;i < weight.length;i++){//i物品范围
        for(int j = 1;j < bagSize + 1;j++){//j背包重量
            if(j < weight[i]){
                //背包总容量放不下当前物品（只能是不放该物品的最大价值）
                dp[i][j] = dp[i - 1][j];//不放这个物品，背包重量相同时候的最大大小
            }else{
                //背包总重量放得下当前物品 (那就是 1.不放该物品 2.放该物品  取最大价值情况)
                dp[i][j] = Math.max(dp[i - 1][j],dp[i - 1][j - weight[i]] + value[i]);//不放该物品背包重量相同时的最大价值  与 放该物品最大价值大小（去除该物品前背包的最大价值）
            }
        }
    }

for(int i = 0;i < dp.length;i++){
     for(int j = 0;j < dp[0].length;j++){
         System.out.print(dp[i][j] + " ");
     }
     System.out.println();
    }
}

4. 算法坑点

1. 初始化，当物品范围为第一个物品时，背包大小大于等于第一个物品的重量时，接下来的全部可以初始化为第一个物品的价值。
2. 递推公式有条件，
   当前物品大小>背包总容量，dp[i][j]=dp[i - 1][j]
   当前物品大小<=背包总容量，dp[i][j]=max(dp[i - 1][j],dp[i - 1][j - weight[i]] + value[i])