大家好，这里是大话硬件。

根据上一篇文章的分析，开关电源系统主要分为3个部分，功率级，控制级，反馈级。今天这篇文章我们分析功率级和控制级的传递函数。

1.功率级传递函数

从功能框图上可以看出来，功率级主要包含两个部分，一个是电源输入通过MOS管开关，得到电压V1，这个电压其实就是我们经常测试的VSW；另外一个是V1经过LC后，得到的输出电压Vo。因此在求解功率级的传递函数时，需要分开来求。

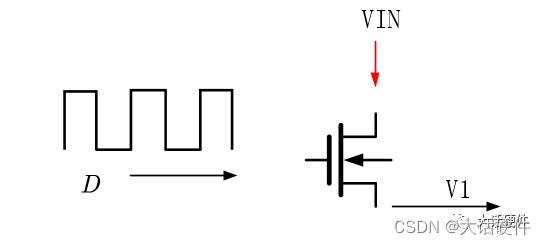
当使用占空比为D的PWM驱动MOS管的时候，输出电压V1的幅值等于VinxD，因此传递函数等于常数Vin。输入电压到V1电压传递函数如下：

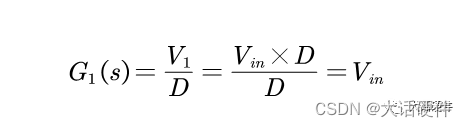
功率级的后半部分是LC滤波电路，根据LCR串并联，可以计算出传递 函数为：

2.控制级传递函数

控制级的输入为误差电压，输出为占空比，在求解该部分传递函数时需要借助下面的图进行分析。

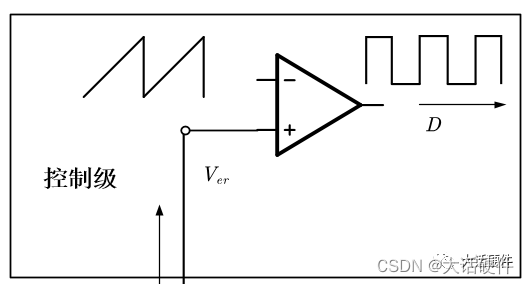
从上面的分析可知，传递函数的输入是误差电压，输出是占空比。

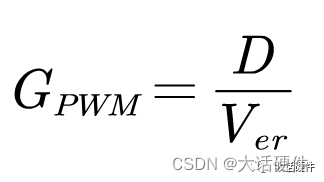
在下面的图中根据三角形相似可以得到

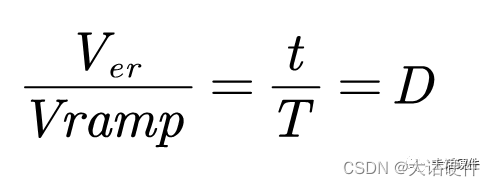
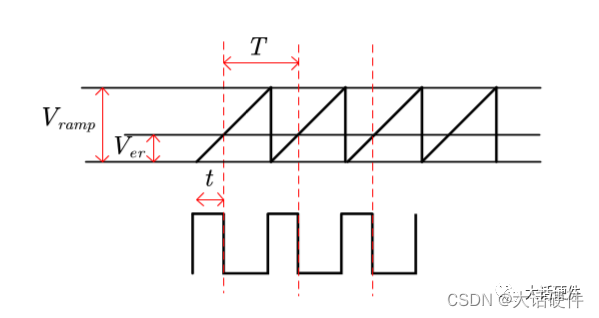
因此，控制级的传递函数为：

3.控制级和功率级传递函数

结合前面的分析，将控制级，功率级的传递函数进行求解为：

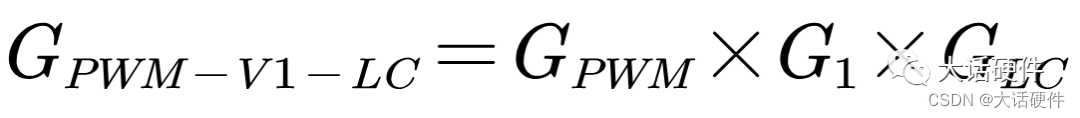
将前面求解的结果代入总的传递函数里面，可以得到：

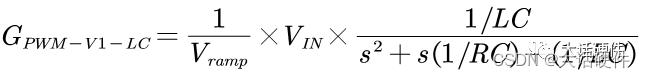
所以，上面的传递函数就是不带反馈的开关电源的传递函数。我们对这个传递函数设定一些参数并进行仿真。

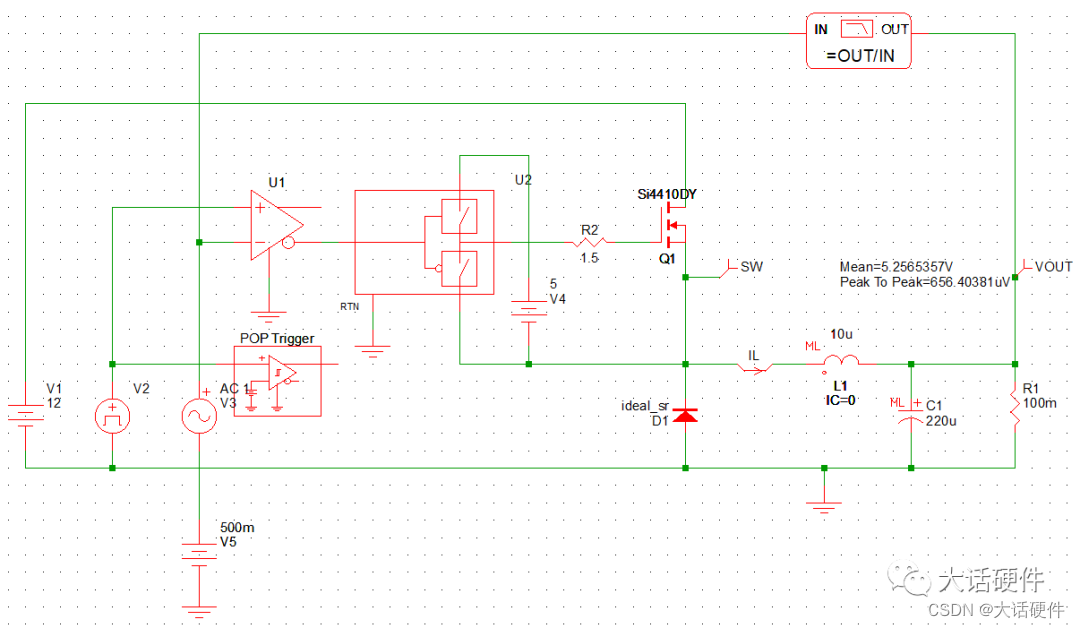
假设这个电源输入12V，占空比50%，输出应该为6V，仿真数据如下：

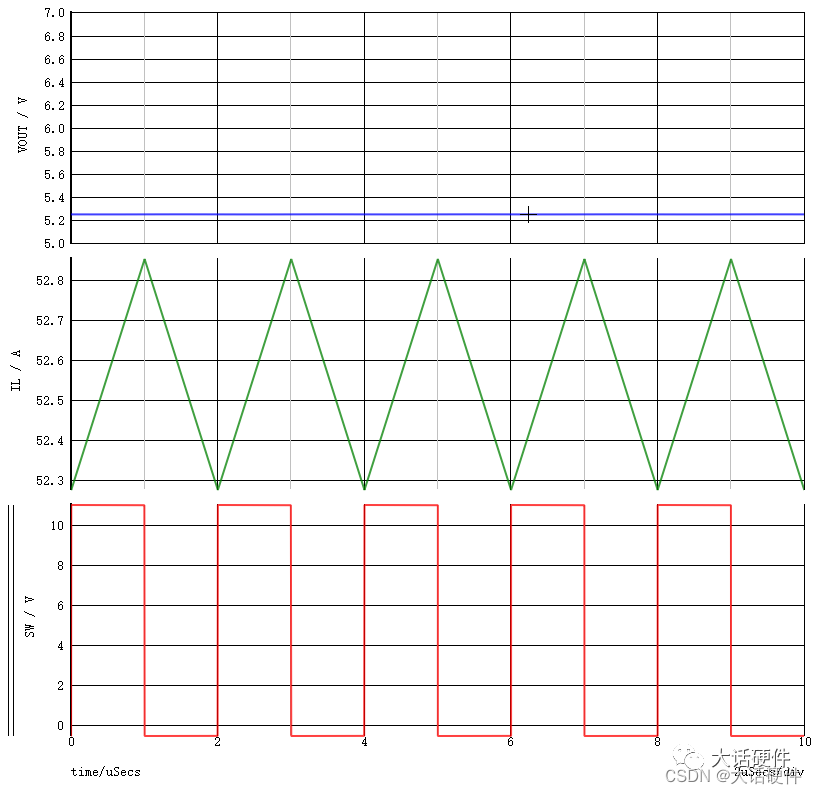
从上面看出，输出电压在5.2V和6V相差0.8V左右。这个差异主要因设定的误差电压和电源不稳定决定。

此时仿真出开环电源的波特图，从波特图上可以明显的看出，在超过2KH，增益以-40dB/dec的斜率下降，在50KHz组左右相位到达了-180°，很明显这个电源是不稳定的。

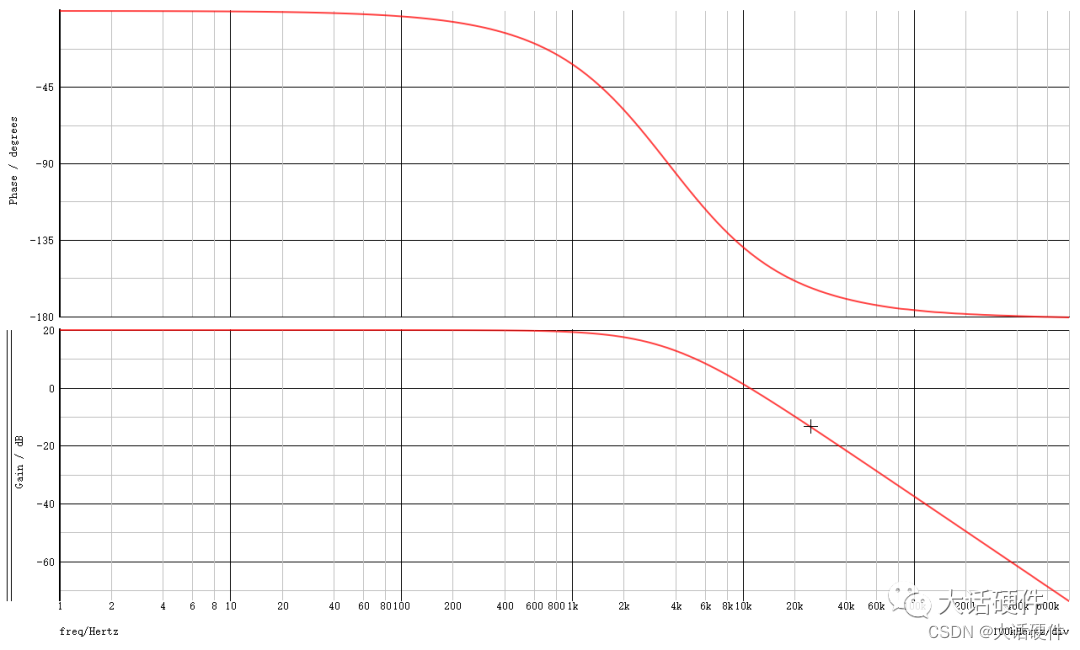
下面我们再看传递函数：

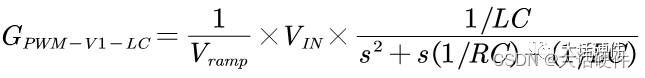
传递函数前面的Vin/Vramp是直流增益，和增益曲线前面一段直线相吻合；传递函数后面是随着频率变化的LC二阶滤波器，二阶滤波器会在-3dB之后以-2的斜率下降，也就是-40dB/dec；单个容抗或者感抗元件带来的相位是-90°，电感和电容会带来-180°的相移。

仿真的结果和上面求解的传递函数是一致的。这也再次证明了，研究传递函数是分析开关电源环路稳定性非常有用的一个工具！

下一篇文章的内容就是分析反馈级不同形式的补偿网络的传递函数。