目录
一、基本思想
二、样例
三、程序
1、普通的深度优先搜索
2、分析
3、记忆化搜索 程序
四、实际速度样例
一、基本思想
今天我们来讲一下深搜的剪枝方法中的一个:记忆化搜索。
顾名思义,记忆化搜索就是让程序记住一些东西,然后可以在需要用的时候可以瞬间调用,不需要再进行一次复杂的计算!
怎么记?
首先,记忆需要大脑来存储数据,什么来模拟大脑? 数组
其次,记忆需要现有的知识用来记住,知识从哪里来? 以前求出的数据
这样,我们如果要用到以前求过的数据,就可以从数组中调用,可以大大提高我们程序的运行速度。
二、样例
斐波那契数列计算:斐波那契数列是这样的:1、1、2、3、5、8、13、21、34……
发现规律了吗? 第一项和第二项是1,除了前面两个数外,每一个数都是前面两个数的和。
这样的题大家应该都做过,现在我们规定一下输入输出格式。
输入格式:
一个正整数N(1≤N≤90)表示输出斐波那契数列的前N项。
输出格式:
共 N 行,每行两个正整数 i、t,表示斐波那契数列第 i 项是 t。
输入样例:
90输出样例:
1 1
2 1
3 2
4 3
5 5
6 8
7 13
8 21
9 34
10 55
11 89
12 144
13 233
14 377
15 610
16 987
17 1597
18 2584
19 4181
20 6765
21 10946
22 17711
23 28657
24 46368
25 75025
26 121393
27 196418
28 317811
29 514229
30 832040
31 1346269
32 2178309
33 3524578
34 5702887
35 9227465
36 14930352
37 24157817
38 39088169
39 63245986
40 102334155
41 165580141
42 267914296
43 433494437
44 701408733
45 1134903170
46 1836311903
47 2971215073
48 4807526976
49 7778742049
50 12586269025
51 20365011074
52 32951280099
53 53316291173
54 86267571272
55 139583862445
56 225851433717
57 365435296162
58 591286729879
59 956722026041
60 1548008755920
61 2504730781961
62 4052739537881
63 6557470319842
64 10610209857723
65 17167680177565
66 27777890035288
67 44945570212853
68 72723460248141
69 117669030460994
70 190392490709135
71 308061521170129
72 498454011879264
73 806515533049393
74 1304969544928657
75 2111485077978050
76 3416454622906707
77 5527939700884757
78 8944394323791464
79 14472334024676221
80 23416728348467685
81 37889062373143906
82 61305790721611591
83 99194853094755497
84 160500643816367088
85 259695496911122585
86 420196140727489673
87 679891637638612258
88 1100087778366101931
89 1779979416004714189
90 2880067194370816120
三、程序
1、普通的深度优先搜索
#include <iostream>
#include <cstdio>
using namespace std;
int n;
long long fbnq(int n)
{
if (n==1 || n==2)
return 1;
return fbnq(n-1)+fbnq(n-2);
}
int main()
{
cin >>n;
for (int i=1;i<=n;i++)
cout <<i <<" " <<fbnq(i) <<endl;
return 0;
}2、分析
运行一下,发现前面 40 项还好,到了后面,速度就突然下降,90项的话大概要2000000年!
那么,我们该怎么办?
我们可以对这个程序计算过的数进行观察(假设当前要计算的是 fbnq(7) ):
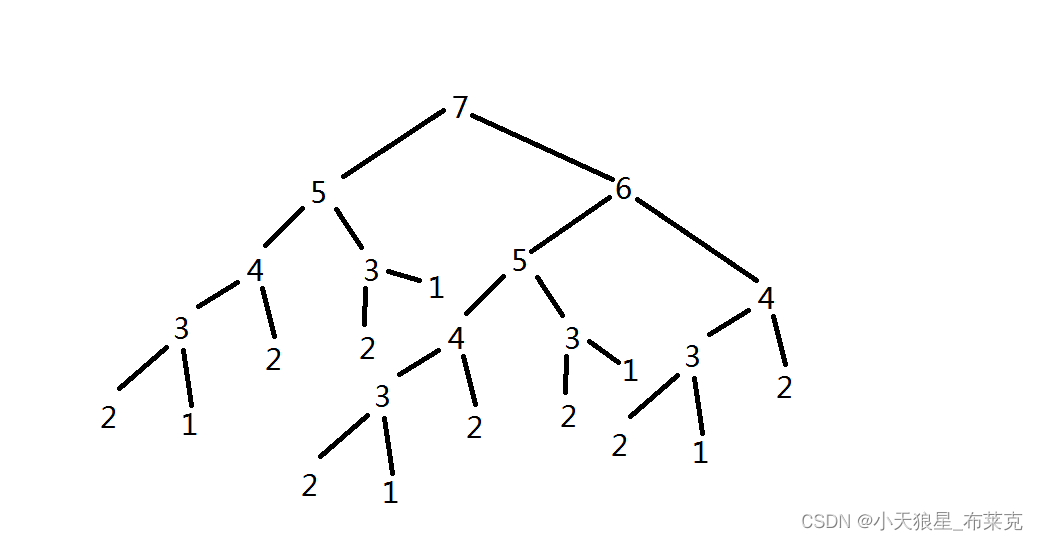
我们发现,这幅图中:
7 被算了 1 次;
6 被算了 1 次;
5 被算了 2 次;
4 被算了 3 次;
3 被算了 5 次;
2 被算了 8 次;
1 被算了 5 次;
这个增长率是非常可观的,除了最后一项,其他的数据正好是 斐波那契数列。
我们知道 斐波那契数列 到达第47项,就可以超过 int 范围! 第93项就可以超过 long long 范围!
这么大的数,怎么可能不超时?
再想一想,同样的东西算了很多遍,为什么不用 “大脑” 将它们 记下来呢? 这样就不用重复计算,只需要直接调用就可以了!!!
OK呀!
3、记忆化搜索 程序
#include <iostream>
#include <cstdio>
using namespace std;
long long n,a[100]; //数组a 为大脑,这里一点要用 long long,原因自己想
long long fbnq(int n)
{
if (n==1 || n==2) //前两项都是 1
return 1;
if (!a[n]) //如果记忆为空
a[n]=fbnq(n-1)+fbnq(n-2); //记住这个值
return a[n]; //返回记忆中的值
}
int main()
{
cin >>n;
for (int i=1;i<=n;i++)
cout <<i <<" " <<fbnq(i) <<endl; //输出
return 0;
}这可能有人要问:为什么不直接用循环搞定呢,又方便又快捷??
是的,一个循环确实方便许多,但这里主要讲的是方法,这个方法在面对 用深度优先搜索 解决 但是会超时 的题目时,可能用得上。
四、实际速度样例
看着这两个截然不同的效率,我不禁想到了什么……
#include <bits/stdc++.h>
#include <windows.h>
using namespace std;
long long n,a[11000];
long long fbnq1(int n)
{
if (n==1 || n==2)
return 1;
if (!a[n])
a[n]=fbnq1(n-1)+fbnq1(n-2);
return a[n];
}
long long fbnq2(int n)
{
if (n==1 || n==2)
return 1;
return fbnq2(n-1)+fbnq2(n-2);
}
void xy(int y,int x)
{
COORD coord;
coord.X=x;
coord.Y=y;
HANDLE a=GetStdHandle(STD_OUTPUT_HANDLE);
SetConsoleCursorPosition(a,coord);
}
int main()
{
system("mode con cols=180 lines=50");
srand (time(0));
cout <<"别人的涨粉速度:\n\n";
system ("pause");
system ("cls");
for (int i=1;i<=10000;i++)
{
fbnq1(i);
xy(rand()%45,rand()%170);
cout <<"+" <<rand()%3+1;
xy(rand()%45,rand()%170);
cout <<" ";
}
Sleep (200);
system ("cls");
cout <<"我的涨粉速度:\n\n";
system ("pause");
system ("cls");
for (int i=1;i<=43;i++)
{
fbnq2(i);
xy(rand()%45,rand()%170);
cout <<"+" <<rand()%3+1;
}
Sleep (200);
system ("cls");
cout <<"生动形象……";
Sleep(1000000);
xy(49,179);
return 0;
}
看我如此可怜,为什么不给我一个三连呢,又不费什么事……



![[附源码]JAVA毕业设计-心理健康管理-(系统+LW)](https://img-blog.csdnimg.cn/7444b85f87c84c4f90a1716b06b6193b.png)