目录
1.算法描述
2.仿真效果预览
3.MATLAB核心程序
4.完整MATLAB
1.算法描述
首先区分大类的话采用的基于功率谱提取的len参数(峰值频率间隔),用峰值个数来代替,这样能很好的区分大类把MFSK和MPSK信号区分开。
针对MPSK:
一:基于瞬时参数——Char2你采用的这个是零中心非弱信号段瞬时相位非线性分量的标准偏差,这个是用来区分2PSK和4PSK的。
二:高阶累积量——针对MPSK高阶累积量的组合在高斯噪声以及多径下能较好的区分MPSK信号。
三:谱相关系数——参考文献(1)中基于谱相关的调制识别,采用谱相关系数在的最大值C可区分2PSK和4PSK。(文献1中4.3节中4.3.2的第四个特征参数)
四:循环累积量——针对MPSK循环累积量在多径下识别率较高,主要是计算量大,复杂度高的特点,区分效果和高阶累积量相同,也是具有抗多径的效果。
五:小波——参考文献(2)针对MPSK的调制识别,码元交界处有幅度不同的跳变,跳变的幅度个数表征PSK的调制阶数,这种特征提取需要进行符号速率估计!(文献2中5.1.4节PSK中的信号阶数判别)
六:M次方谱——参考文献(3),对于BPSK信号的平方谱在2倍载频处有很强的单频分量,其他的PSK信号无此特性,QPSK信号的四次方谱在2倍载频处有单频分量,所以M次方谱的单频分量的检测可以区分信号MPSK信号。
广义回归神经网络是径向基神经网络的一种,GRNN具有很强的非线性映射能力和学习速度,比RBF具有更强的优势,网络最后普收敛于样本量集聚较多的优化回归,样本数据少时,预测效果很好,还可以处理不稳定数据。虽然GRNN看起来没有径向基精准,但实际在分类和拟合上,特别是数据精准度比较差的时候有着很大的优势。
GRNN是RBF的一种改进,结构相似。区别就在于多了一层求和层,而去掉了隐含层与输出层的权值连接(对高斯权值的最小二乘叠加)。
1.输入层为向量,维度为m,样本个数为n,线性函数为传输函数。
2.隐藏层与输入层全连接,层内无连接,隐藏层神经元个数与样本个数相等,也就是n,传输函数为径向基函数。
3.加和层中有两个节点,第一个节点为每个隐含层节点的输出和,第二个节点为预期的结果与每个隐含层节点的加权和。
4.输出层输出是第二个节点除以第一个节点。
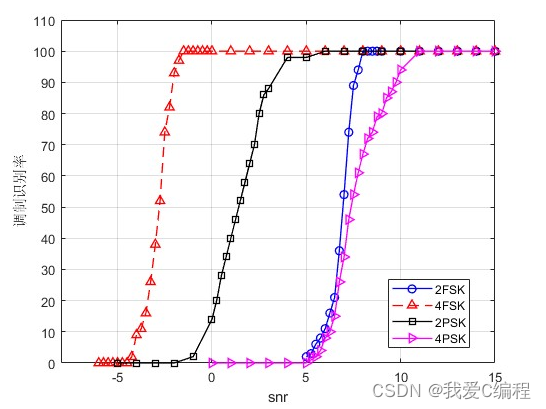
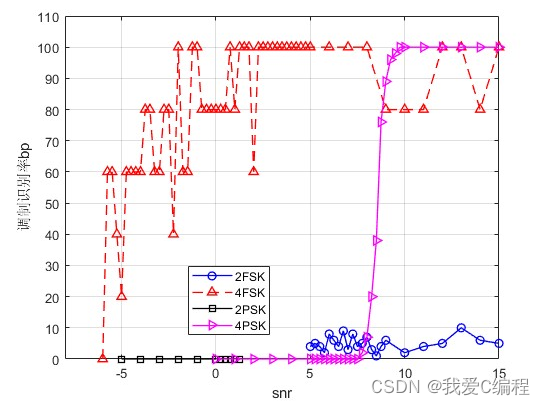
2.仿真效果预览
matlab2022a仿真结果如下:

3.MATLAB核心程序
clc;
clear;
close all;
warning off;
addpath 'func\'
%全局变量
parameters;
SNR0 = inf;
N0 = 50000;
y_2FSK = zeros(1,N0);
y_4FSK = zeros(1,N0);
y_2PSK = zeros(1,N0);
y_4PSK = zeros(1,N0);
%2FSK
y_2FSK = func_2FSK(N0);
%4FSK
y_4FSK = func_4FSK(N0);
%BPSK
y_2PSK = func_2PSK(N0);
%QPSK
y_4PSK = func_4PSK(N0);
%调制识别
y_2FSKn = func_add_noise(y_2FSK,SNR0);
y_4FSKn = func_add_noise(y_4FSK,SNR0);
y_2PSKn = func_add_noise(y_2PSK,SNR0);
y_4PSKn = func_add_noise(y_4PSK,SNR0);
%首先进行FSK和PSK两种模式的区分
Ns = 2048;
%用x进行功率谱估计
[p1,f1] = func_power(y_2FSKn,Ns);
[p2,f2] = func_power(y_4FSKn,Ns);
[p3,f3] = func_power(y_2PSKn,Ns);
[p4,f4] = func_power(y_4PSKn,Ns);
len1 = func_fsk_psk_check(p1);
len2 = func_fsk_psk_check(p2);
len3 = func_fsk_psk_check(p3);
len4 = func_fsk_psk_check(p4);
%根据参数获得FSK和PSK区分参数
Level= (mean([len1,len2]) - mean([len3,len4]))/2;
%分别提取FSK和PSK的不同调制方式的特征参数
char1 = real(func_para_check(y_2FSKn,N0));
char2 = real(func_para_check(y_4FSKn,N0));
char3 = real(func_para_check(y_2PSKn,N0));
char4 = real(func_para_check(y_4PSKn,N0));
%通过GRNN神经网络进行训练
char = [char1;char2]';
T = [1;2]';
net_fsk = newgrnn(char,T,1.2);
char = [char3;char4]';
T = [1;2]';
net_psk = newgrnn(char,T,1.2);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%加载信号进行测试
%通过大量的循环测试,计算正确率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
zql = 0;
%运行的时候,尽量将下面的两个参数指标设置大点,这样结果才精确
MTKL = 100;
SNRS = [5:0.25:9,10:15];
Bers = zeros(length(SNRS),1);
for jj = 1:length(SNRS)
for i = 1:MTKL
SNRS(jj)
i
s = RandStream('mt19937ar','Seed',i);
RandStream.setGlobalStream(s);
%长度
N = N0;
%SNR
SNR = SNRS(jj);
%2FSK
y_2FSK = func_2FSK(N);
%4FSK
y_4FSK = func_4FSK(N);
%BPSK
y_2PSK = func_2PSK(N);
%QPSK
y_4PSK = func_4PSK(N);
%设置单独的一种调制信号
tmps = [1,1,1,1];%2FSK
if tmps(1) == 1
datas = y_2FSK;
end
if tmps(1) == 2
datas = y_4FSK;
end
if tmps(1) == 3
datas = y_2PSK;
end
if tmps(1) == 4
datas = y_4PSK;
end
datas = func_multipath(datas);
data = func_add_noise(datas,SNR);
[p,f] = func_power(data,Ns);
len = func_fsk_psk_check(p);
flag = 0;
%首先进行FSK和PSK两种模式的区分
if len >= Level%为FSK模式
%根据识别参数进行调制类型的辨识
char = real(func_para_check(data,length(data)));
T = round(sim(net_fsk,char'));
if T == 1
flag = 1;
end
if T == 2
flag = 2;
end
else%为PSK模式
%根据识别参数进行调制类型的辨识
char = real(func_para_check(data,length(data)));
T = round(sim(net_psk,char'));
if T == 1
flag = 3;
end
if T == 2
flag = 4;
end
end
if flag == tmps(1)
zql = zql + 1;
end
end
%识别正确率
Bers(jj) = zql/MTKL;
zql = 0;
end
R = 100*mean(Bers,2);
01-126m4.完整MATLAB
V