【LeetCode】1691. 堆叠长方体的最大高度

news2024/11/16 3:51:19

题目描述

给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [width_i, length_i, height_i]（下标从 0 开始）。请你从 cuboids 选出一个子集，并将它们堆叠起来。
如果 width_i <= width_j 且 length_i <= length_j 且 height_i <= height_j ，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。
返回堆叠长方体 cuboids 可以得到的最大高度。

示例 1：

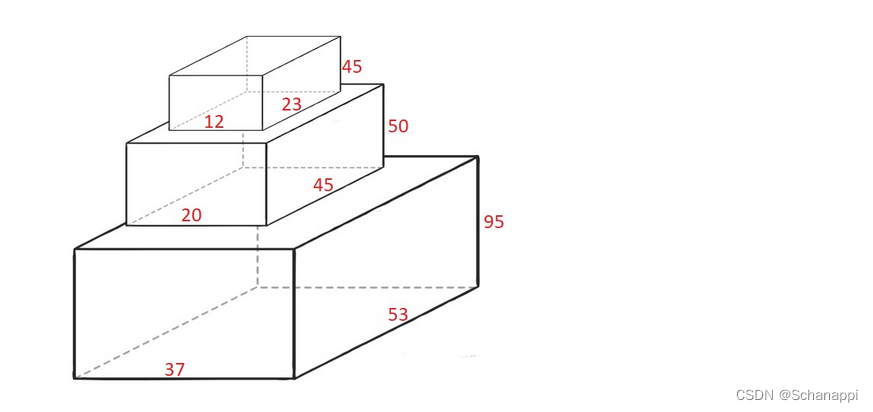
输入：cuboids = [[50,45,20],[95,37,53],[45,23,12]]
输出：190
解释：
第 1 个长方体放在底部，53x37 的一面朝下，高度为 95 。
第 0 个长方体放在中间，45x20 的一面朝下，高度为 50 。
第 2 个长方体放在上面，23x12 的一面朝下，高度为 45 。
总高度是 95 + 50 + 45 = 190 。

示例 2：

输入：cuboids = [[38,25,45],[76,35,3]]
输出：76
解释：
无法将任何长方体放在另一个上面。
选择第 1 个长方体然后旋转它，使 35x3 的一面朝下，其高度为 76 。

示例 3：

输入：cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
输出：102
解释：
重新排列长方体后，可以看到所有长方体的尺寸都相同。
你可以把 11x7 的一面朝下，这样它们的高度就是 17 。
堆叠长方体的最大高度为 6 * 17 = 102 。

提示：

n == cuboids.length
1 <= n <= 100
1 <= width_i, length_i, height_i <= 100

方法一：

思路：

首先对每个长方体三个维度的长度进行排序，将最长的放置在最前面，那么 cuboids[i][0] 就会作为高度累加到最终结果；
对每个长方体内部进行排序之后，对所有长方体进行升序排序，也就是说，后一个长方体才可能叠加在前一个长方体之上。
完成排序工作后，开始遍历每一个长方体。使用 动态规划 的思想， dp[i] 指的是前 i 个长方体的最大高度。
因此，先令 dp[i] = cuboids[i][0]，这对应了不堆叠的情况；
之后，因此遍历当前能够堆叠的长方体，如果能够堆叠，则有 dp[i] = max(dp[i], dp[j] + cuboids[i][0]) 。
最后， max_height = max(max_height, dp[i]) ，因为 dp[n-1] 很有可能不是高度最大的情况，所以在过程中要保存当前的最大高度。

情况

通过；

收获

今天终于用上了 动态规划 ，思路也比较顺利，但是出现了一些问题：
对每个长方体内部排序的时候，对于 for(auto ) 忘记加上 & ，导致排序一直无法生效；
对所有长方体排序的时候，由于每个长方体数组内还有三个元素，应该要另外写函数才能保证降序排序，这里偷懒了，因此使用了默认的升序排序，不过问题不大。
对 动态规划 中情况的考虑不够充分，一开始想的是按顺序不断累加，但其实 i=2 和 i=4 也可以累加，因此还是需要双重循环。

时间复杂度：O（n²），其中 n 表示长方体的个数。时间复杂度主要取决于排序与动态规划枚举，对每个长方体边的大小进行排序的总时间复杂度为 O(n)，对长方体进行排序的时间为 O(n logn)，对于每个长方体我们都需要枚举所有可以堆叠其上的长方体，需要的时间为O(n²)，因此总的时间复杂度为 O(n²) 。
空间复杂度：O（n），其中 n 表示长方体的个数。排序需要的栈空间为 O(log n)，存储每个长方体为底的最大高度需要的空间为 O(n)，因此总的空间复杂度为 O(n)。

class Solution {
public:
    int maxHeight(vector<vector<int>>& cuboids) {
        // 对长方体的长宽高按大->小排序 cuboid[0]:height
        for(auto& cub : cuboids){
            sort(cub.begin(), cub.end(), greater<int>());
        }
        // 对所有长方体排序，按照从小到大
        sort(cuboids.begin(), cuboids.end());
        int n = cuboids.size();
        int max_height = 0;
        vector<int> dp(n);
        for(int i=0; i<n; i++){
            dp[i] = cuboids[i][0];
            for(int j=0; j<i; j++){
                // 能堆叠
                if(cuboids[j][0] <= cuboids[i][0] && 
                   cuboids[j][1] <= cuboids[i][1] && 
                   cuboids[j][2] <= cuboids[i][2]){
                    dp[i] = max(dp[i], dp[j] + cuboids[i][0]);
                }
            } 
            max_height = max(max_height, dp[i]);
        }
        return max_height;
    }
};