【负荷预测】基于贝叶斯网络的考虑不确定性的短期电能负荷预测（Python代码实现）

news2024/10/5 8:18:38

👨‍🎓个人主页：研学社的博客

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🌈3 Matlab代码实现

🎉4 参考文献

💥1 概述

短期电力负荷预测是现代电力系统控制与运行分析的一项重要研究内容。随着电力体制改革的深化,电力市场的不断完善以及智能电,网建设目标的逐步实施,电网运行中对于经济性和安全性的要求越来越高,对短期负荷预测也提出了更高的要求。
传统预测方法由于其原理比较简单,理论相对成熟,因此至今仍被广泛应用。传统预测方法主要有:趋势外推法、时间序列法、回归分析法等。由于电力负荷有着非线性、时变性和不确定性的特点,而传统预测方法采用的数学模型过于简单.不能及时、准确地对预测模型的参数进行估计和调整,更不能方便描述负荷的突然变化,从而使这些方法难以获得较高的预测精度。随着负荷预测技术研究的不断深化,相继出现了以人工智能为代表的负荷预测新方法.如:灰色预测法[1、模糊预测法!2!、优选组合法[31、小波分析法!4和人工神经网络法等。由于一些方法考虑了负荷预测系统的鲁棒性,并且能够拟合出负荷的复杂非线性关系,因此,人工智能方法与传统方法相比有许多优点。

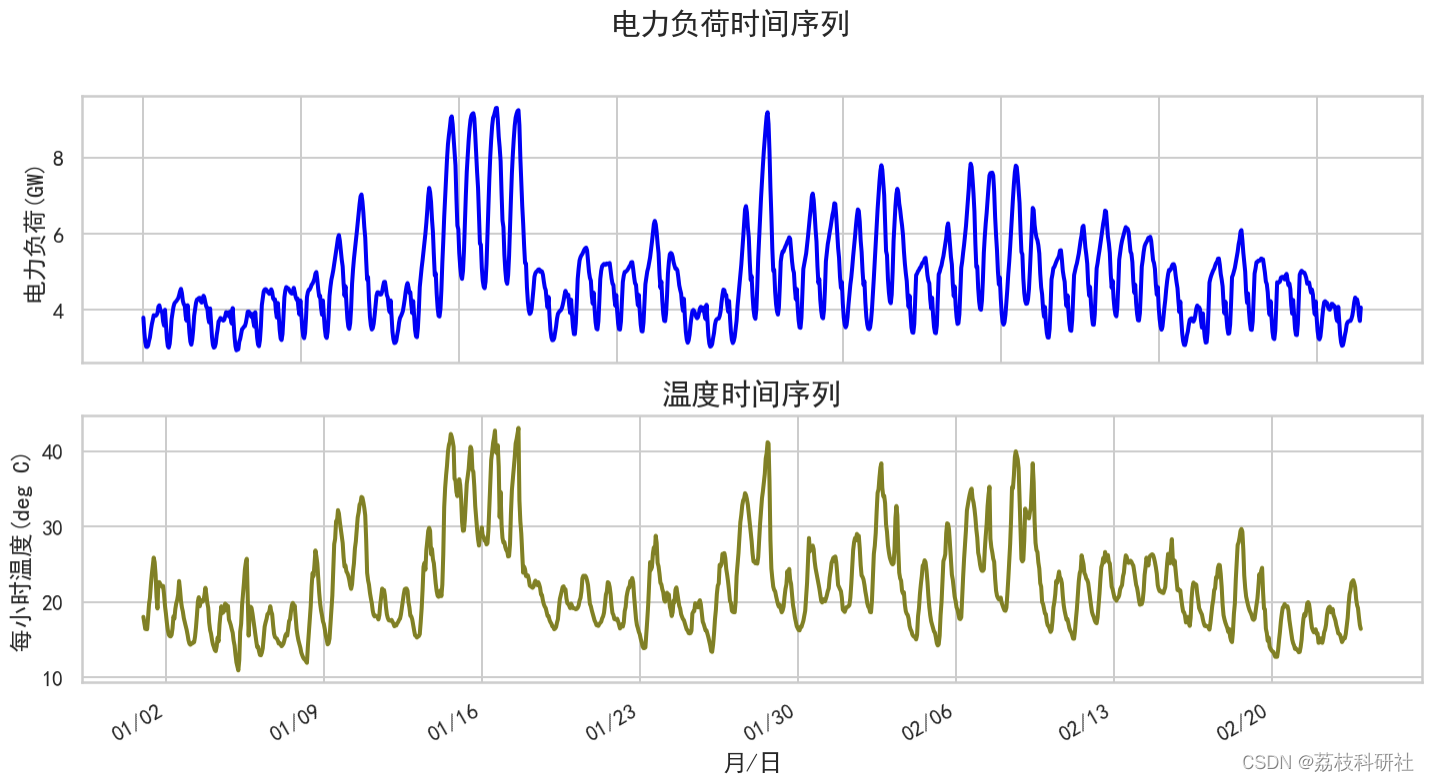
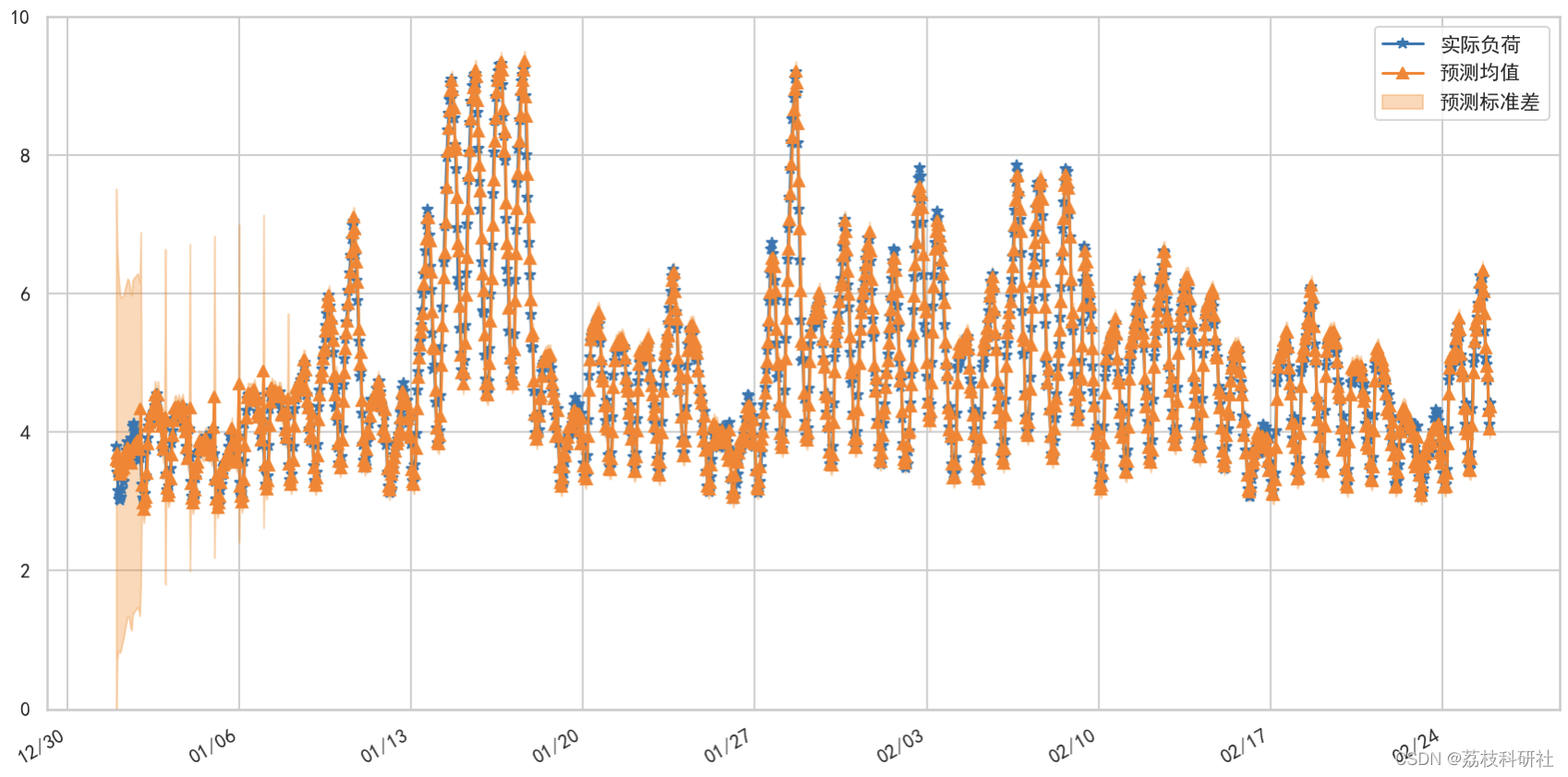
📚2 运行结果

print('偶然不确定性:',std_mean)
print('认知不确定性:',mean_sigma)

print('偶然不确定性:',np.mean(std_mean))
print('认知不确定性:',np.mean(mean_sigma))

结果：

偶然不确定性: [0.37458175 0.37458175 0.37458175 0.37461463 0.38332063 0.4107164
 0.45222163 0.48494232 0.5312848  0.5443692  0.58056927 0.6104524
 0.6372883  0.6621181  0.6731655  0.6266249  0.63724846 0.65924484
 0.6147452  0.57374454 0.5360238  0.5130135  0.4896349  0.4747888 ]
认知不确定性: [0.0162899  0.0162899  0.0162899  0.01622007 0.06685151 0.0674182
 0.06788017 0.03853567 0.04431767 0.04643966 0.05136628 0.05558429
 0.05943689 0.06303471 0.06498456 0.06015231 0.06211003 0.06539844
 0.06097266 0.05708234 0.05377384 0.0522627  0.0508984  0.05050901]
偶然不确定性: 0.5247449
认知不确定性: 0.050170798

部分代码：

y_stds = np.concatenate(y_pred_stds, axis=1)
std_mean = np.mean(y_stds, axis=1) #Aleatoric uncertainty
std_sigma = np.std(y_stds, axis=1)
fig=plt.figure(figsize=(12, 6),dpi=200)
ax = fig.add_subplot(1,1,1)
ax.fill_between(test_dates,
                 mean_mean + 2*mean_sigma,
                 mean_mean - 2*mean_sigma,
                 alpha=0.9, label='认知不确定性')
ax.fill_between(test_dates,    
                 mean_mean + std_mean,  # Aleatoric uncertainty 条件均值的方差
                 mean_mean - std_mean,
                 alpha=0.5, label='偶然不确定性')
ax.plot(test_dates,y_test,label='实际负荷',marker='*')
ax.plot(test_dates, test_mean, 'r-', label='预测均值',marker='^');
#plt.title('2月24日ＢＮＮ日前电力负荷预测不确定性表示')
ax.xaxis.set_major_locator(test_loc)
ax.xaxis.set_major_formatter(test_fmt)
ax.set_ylabel("电力负荷(GW)")
ax.set_xlabel("时间(H)")
plt.legend()
plt.ylim((2,7))
plt.grid()
plt.show()

y_stds = np.concatenate(y_pred_stds, axis=1)
std_mean = np.mean(y_stds, axis=1) #Aleatoric uncertainty
std_sigma = np.std(y_stds, axis=1)
fig=plt.figure(figsize=(12, 6),dpi=200)
ax = fig.add_subplot(1,1,1)
ax.fill_between(test_dates,
                 mean_mean + 2*mean_sigma,
                 mean_mean - 2*mean_sigma,
                 alpha=0.9, label='认知不确定性')
ax.fill_between(test_dates,    
                 mean_mean + std_mean,  # Aleatoric uncertainty 条件均值的方差
                 mean_mean - std_mean,
                 alpha=0.5, label='偶然不确定性')
ax.plot(test_dates,y_test,label='实际负荷',marker='*')
ax.plot(test_dates, test_mean, 'r-', label='预测均值',marker='^');
#plt.title('2月24日ＢＮＮ日前电力负荷预测不确定性表示')
ax.xaxis.set_major_locator(test_loc)
ax.xaxis.set_major_formatter(test_fmt)
ax.set_ylabel("电力负荷(GW)")
ax.set_xlabel("时间(H)")
plt.legend()
plt.ylim((2,7))
plt.grid()
plt.show()