参考资料：Xilinx FIR Compiler v7.2 LogiCORE IP Product Guide PG149

半带滤波器

半带滤波器的阶数为偶数，系数长度为奇数，且除了中间系数为0.5外，其余偶数序号系数都为0。
系数长度 = 抽头数 = FIR滤波器的阶数 + 1 。
半带滤波器的幅频响应如下图。半带滤波器主要用于2倍的抽取前的滤波。

通带截止频率${\Omega }_p$和阻带起始频率${\Omega }_{st}$关于$\frac{\pi }{2}$(或$\frac{f_s}{4})$对称，且通带纹波等于阻带纹波，即满足如下表达式。
$${\Omega }_p=\pi -{\Omega }_{st},{\delta }_p={\delta }_s$$

针对一个抽头数为11的半带滤波器其脉冲响应和FPGA实现结构如下图。

针对滤波器系数的对称性还可以优化实现结构。第一幅图针对奇数抽头，第二幅图针对偶数抽头。

以AD9361的接收信号链路中用于2倍抽取的Rx HB1为例。其系数为[-8, 0, 42, 0, -147, 0, 619, 1013, 619, 0, -147, 0, 42, 0, -8]。

h = [-8, 0, 42, 0, -147, 0, 619, 1013, 619, 0, -147, 0, 42, 0, -8];
[H,W] = freqz(h);
Hf = abs(H);% 幅频响应
Hx = angle(H);% 相频响应
plot(W,Hf/max(Hf));% 归一化幅频响应

AD9361中用于3倍抽取时的Rx DEC3系数为 [55, 83, 0, -393, -580, 0, 1914, 4041, 5120, 4041, 1914, 0, -580, -393, 0, 83, 55]。同样画出其归一化幅频响应，标记出关键点。

有数字信号处理理论：
$$x(n)\to H_D(e^{j\omega })\to \downarrow D\to x_D(m)$$
其中$$\left|H_{\mathrm{D}}\left({\mathrm{e}}^{\mathrm{j}\omega }\right)\right|=\{\begin{array}{ll}D& |\omega |<\pi /D\\ 0& \pi /D⩽|\omega |<\pi \end{array}$$

多相抽取滤波器

下图为一个M倍抽取的多相抽取滤波器结构示意图。

其中$N$个原滤波器系数$a(0),a(1),\cdots ,a(N-1)$被映射到$M$个多相子滤波器系数$h_0(n),h_1(n),\cdots ,h_{M-1}(n)$，两者关系如以下公式。
$$h_i(r)=a(i+Mr)i=0,1,\cdots ,M-1r=0,1,\cdots ,\frac{N}{M}$$
例如$$\begin{array}{c}\\ h=[a,b,c,d,e,f,g,h,g,f,e,d,c,b,a]，M=3\\ h_0=[a,d,g,f,c]\\ h_1=[b,e,h,e,b]\\ h_2=[c,f,g,d,a]\end{array}$$
多相抽取滤波器通过输入换向器将输入样本$x(n)$送入多相子滤波器，换向器索引从$M-1$递减到$0$。在换向器执行了一个周期并向滤波器组提供了$M$个输入样本后，各多相子滤波器的输出之和作为一个输出样本$y(n)$。则$y(n)$的输出采样率为$f_s/M$。

多相内插滤波器

下图为一个P倍内插的多相内插滤波器结构示意图。

其中$N$个原滤波器系数$a(0),a(1),\cdots ,a(N-1)$被映射到$P$个多相子滤波器系数$h_0(n),h_1(n),\cdots ,h_{P-1}(n)$，两者关系如以下公式。
$$h_i(r)=a(i+Pr)i=0,1,\cdots ,P-1r=0,1,\cdots ,\frac{N}{P}$$
多相内插滤波器的每一个输入样本$x(n)$都要送入到各个多相子滤波器，一个输入样本$x(n)$经过多相内插滤波器后对应$P$个输出样本$y(n)$。输出采样率为$P\times f_s$。

半带抽取器和半带内插器

结合前面所述，半带抽取器和内插器就将半带滤波器与多相滤波器结合起来。具体结构如下图。


以前面所用的Rx HB1系数为例，其系数为[-8, 0, 42, 0, -147, 0, 619, 1013, 619, 0, -147, 0, 42, 0, -8]。

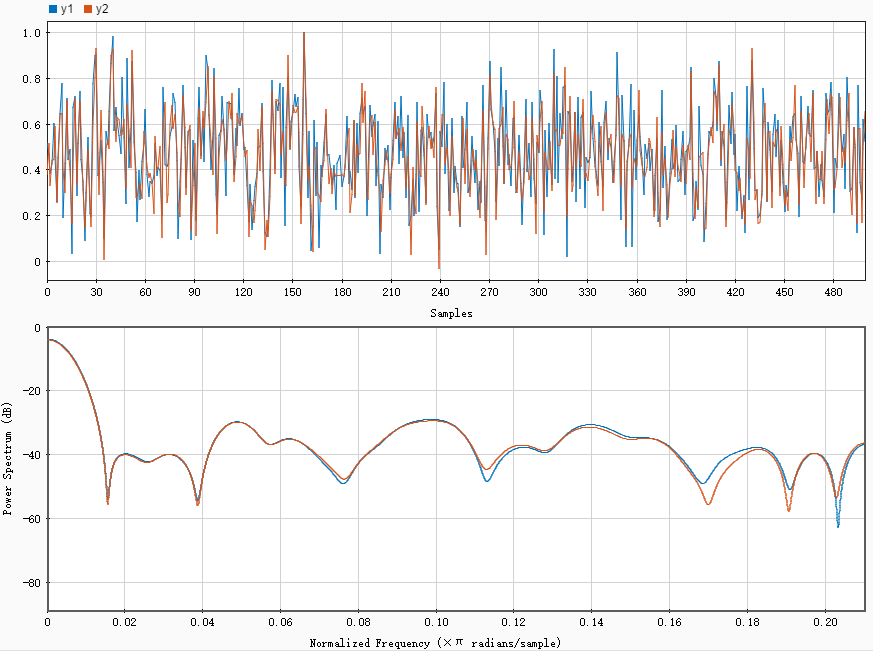
close all; clear;
x = round(rand(1,1000)*5);
h = [-8, 0, 42, 0, -147, 0, 619, 1013, 619, 0, -147, 0, 42, 0, -8];
n = length(h);
h0 = h(1:2:end);
h1 = h(2:2:end);
y1 = conv(x,h);% 先滤波后抽取
y1 = y1(n/2:end-n/2);
y1 = y1(1:2:end);
x_a = x(1:2:end);% 先抽取再滤波
y2_a = conv(x_a,h0); 
y2_a = y2_a(n/4:end-n/4);
x_b = x(2:2:end);
y2_b = conv(x_b,h0);
y2_b = y2_b(n/4:end-n/4);
y2 = y2_a + y2_b;
x = x/max(x);% 归一化
y1 = y1/max(y1);
y2 = y2/max(y2);

通过Matlab信号分析工具箱画出两种方法输出y1和y2的时域图和频域图，可以看到两种方法均可实现2倍的抽取操作，且两者的频域波形相差不大。