参考资料:《深入理解计算机网络(王达)》
文章目录
- 一,数制
- 1.1 基本数制
- 1.2 不同数制之间的相互转换
- 二,编码
一,数制
1.1 基本数制
“数制”是“数据进制”的简称,也就是表示数据逢几进位的意思,如我们常用的十进制就是逢十进位,常见的还有二进制、八进制、十六进制。
- 二进制(Binary),二进制是计算机运算时所采用的的数制类型,基数是2,二进制数的标志为B,如(1001010)B,也可以用下标2来表示;
- 八进制(Octal),八进制的标志为O或Q,如(4603)O、(4603)Q,也可以用下标8来表示;
- 十进制(Decimal),十进制数的标志为D,如(1250)D,也可以用下标10来表示;
- 十六进制(Hexadecilmal),十六进制的标志为H,如(45A)H,也可以用下标16来表示,十六进制也常用前缀0x来表示。
为什么进制采用2、8、16这种,而不是9或12进制呢?
答:2、8、16分别是2的一次、三次、四次方,这就使得这三种进制之间可以很方便的直接进行互相转换。八进制或十六进制缩短了二进制,但保持着二进制的表达特点。
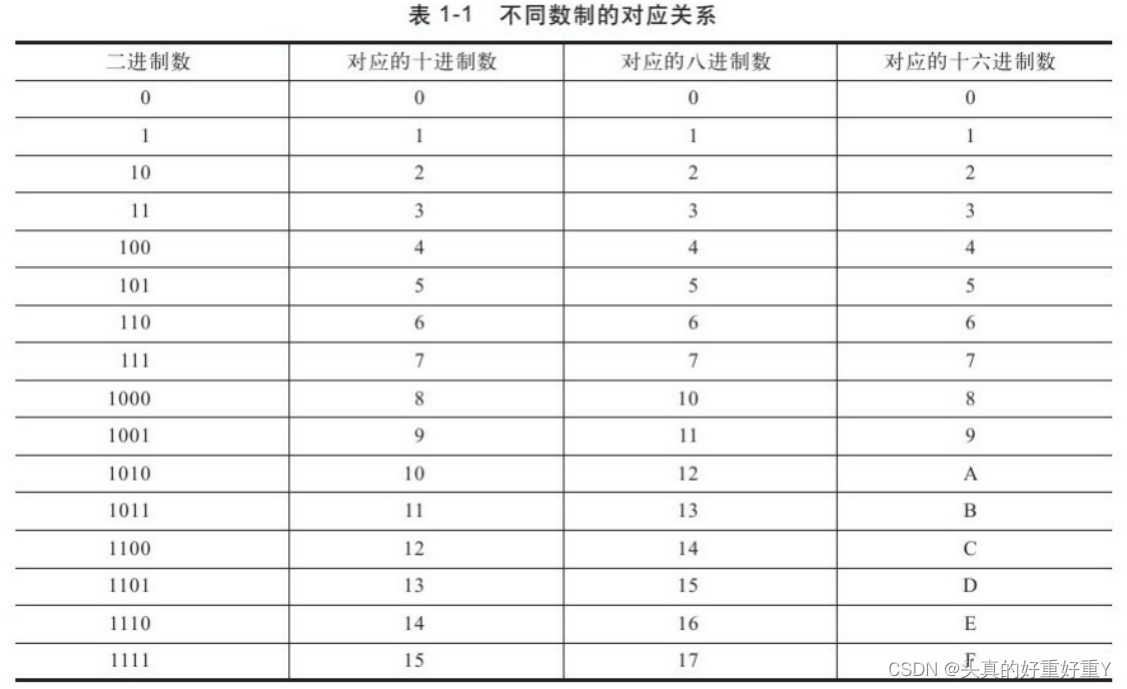
1.2 不同数制之间的相互转换
- 非十进制数转换为十进制数
按权相加法:非十进制数转换为十进制数就是把这些非十进制数按位以对应的权值(注意要区分整数位与小数位)展开,然后相加得出相应的十进制值。

- 十进制数转换为非十进制数
十进制数的整数部分采用“除基逆序取余法”(基数相除,然后逆序取余数),小数部分采用“乘基正序取整法”(基数相乘,然后正序取整数)。这里指的基数就是对应的数制,如二进制的基数为2,八进制基数为8,十六进制基数为16。

- 非进制数之间的相互转换
之前说过,二进制、八进制、十六进制分别是2的一次方、三次方、四次方,因此一位八进制数对应三位二进制数,而一位十六进制数则对应四位二进制数,他们之间的相互转换十分容易。

- 进制转换Java代码:
/**
* 类描述:进制转换器, 编写一个进制转换器, 可以让数字在 二进制, 八进制, 十进制, 十六进制自由转换
**/
public class RadixConversion {
public static void main(String[] args) {
RadixConversion radix = new RadixConversion();
// 11101001000.10111B, 1076O, 6374.65Q, 0X7A8C
radix.conversionDecimal("11101001000.10111B");
// 825D -> B, 10815.6D -> B, 658D -> O, 9240.65D -> O, 2508D -> H, 5420.82D -> H
radix.conversionDRadix("825D", Radix.BINARY);
}
/**
* 1.2.1同步练习: 进制转换, 非十进制数转换为十进制数, 将指定参数转换为十进制(Decimal)标志位为D
* @param str 待转换的参数, 可以是二进制(Binary)标志位为B, 八进制(Octal)标志位为O或Q, 十六进制(Hexadecilmal)标志位为0X或H
* @return
*/
public double conversionDecimal(String str) {
// 1. 首先判断str是什么进制的
String radix = "10";
double result = 0.0;
Map<String, String> map = new HashMap<>();
Map<Character, Integer> hexadecilmalMapping = new HashMap<>();
map.put("B", "2");
map.put("O", "8");
map.put("Q", "8");
map.put("D", "10");
map.put("0X", "16");
hexadecilmalMapping.put('0', 0);
hexadecilmalMapping.put('1', 1);
hexadecilmalMapping.put('2', 2);
hexadecilmalMapping.put('3', 3);
hexadecilmalMapping.put('4', 4);
hexadecilmalMapping.put('5', 5);
hexadecilmalMapping.put('6', 6);
hexadecilmalMapping.put('7', 7);
hexadecilmalMapping.put('8', 8);
hexadecilmalMapping.put('9', 9);
hexadecilmalMapping.put('A', 10);
hexadecilmalMapping.put('B', 11);
hexadecilmalMapping.put('C', 12);
hexadecilmalMapping.put('D', 13);
hexadecilmalMapping.put('E', 14);
hexadecilmalMapping.put('F', 15);
for (Map.Entry<String, String> entry : map.entrySet()) {
if (str.contains(entry.getKey())) radix = entry.getValue();
}
// 2. 根据不同的进制选择不同的分支, 预处理待转换的数据
switch (radix) {
case "2" :
str = str.replace("B", "");
break;
case "8" :
str = str.replace("Q", "");
str = str.replace("O", "");
break;
case "10" :
str = str.replace("D", "");
break;
case "16" :
str = str.replace("0X", "");
str = str.replace("H", "");
break;
}
// 3. 开始转换数据, 要判断有没有小数点的情况, Math.pow(a, b)表示求a的b次幂
String str_cp = str;
double right = 0.0;
if (str.contains(".")) {
str_cp = str.split("\\.")[0];
str = str.split("\\.")[1];
for (int i = 0, j = -1; i < str.length(); i++, j--) {
right += hexadecilmalMapping.get(str.charAt(i)) * Math.pow(Double.parseDouble(radix), j);
}
}
for (int i = 0, j = str_cp.length() - 1; i < str_cp.length(); i++, j--) {
result += hexadecilmalMapping.get(str_cp.charAt(i)) * Math.pow(Double.parseDouble(radix), j);
}
result += right;
System.out.println(result + "D");
return result;
}
/**
* 1.2.2同步练习: 进制转换, 十进制数转换为非十进制数, 将十进制数转换为指定进制数, 使用"除基逆序取余工作"与"乘积正序取整工作"
* @param str 待转换的十进制数
* @param radix 待转换的进制, 枚举类型, Radix.type
* @return 返回radix进制的str
*/
public String conversionDRadix(String str, Radix radix) {
StringBuilder sb = new StringBuilder();
// 1. 去掉十进制数的D符号标注
str = str.replace("D", "");
String str_cp = str;
int base = radix == Radix.BINARY ? 2 : radix == Radix.OCTAL ? 8 : radix == Radix.DECIMAL ? 10 : 16;
String right = "";
// 2. 如果有小数位则需要特殊处理
if (str.contains(".")) {
str_cp = str.split("\\.")[0];
double small = Double.parseDouble("0." + str.split("\\.")[1]);
// 2.1. 待转换的十进制小数部分, 开始小数部分的"乘积正序取整"工作
int i = 0;
// 2.2. 只保留三位小数
while (small > 0 && i < 3) {
i++;
small = small * base;
if (small > 0) {
// 2.3. 此处需要获取small小数的整数位与小数位, 然后赋值给对应的对象, 巧妙的使用int+double类型强转
int count = (int) small;
sb.append(count < 10 ? count
: count == 10 ? "A"
: count == 11 ? "B"
: count == 12 ? "C"
: count == 13 ? "D"
: count == 14 ? "E" : "F");
small = small - count;
}
}
right = "." + sb;
}
sb = new StringBuilder();
// 3. 待转换的十进制整数部分, 开始整数部分的"除基逆序取余"工作
int num = Integer.parseInt(str_cp);
while (num >= base) {
// 3.1. 此处非常巧妙的解决了十六进制中大于等于10的数字需要用字母替代的问题
int count = num % base;
sb.append(count < 10 ? count
: count == 10 ? "A"
: count == 11 ? "B"
: count == 12 ? "C"
: count == 13 ? "D"
: count == 14 ? "E" : "F");
num /= base;
}
if (num > 0) sb.append(num);
// 3.2. 整数部分是需要逆序的, 此处使用reverse反转方法
System.out.println(sb.reverse() + right + " " + radix);
return sb.reverse() + right;
}
/**
* 枚举进制类, 方便标注进制类型
*/
public enum Radix {
// 二进制, 八进制, 十进制, 十六进制
BINARY, OCTAL, DECIMAL, HEXADECILMAL
}
}
二,编码
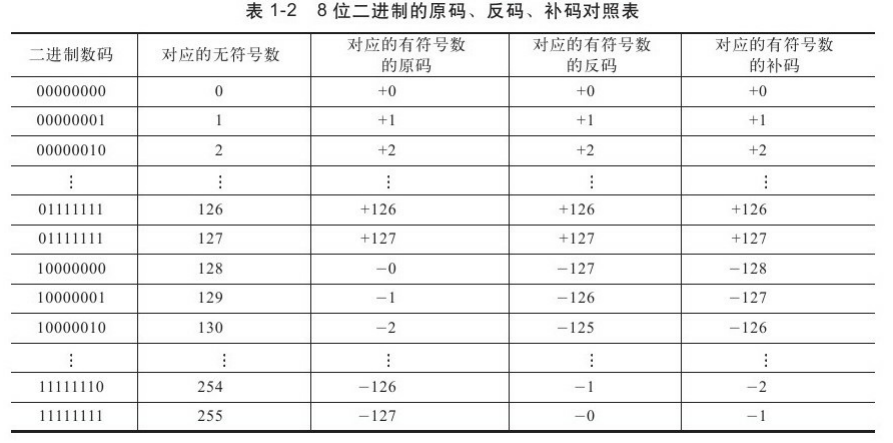
数据编码主要包括“原码”、“反码”、“补码”三种,它们用以不同的形式来表示数据。其实在计算机中负数是以其正数的补码形式来表示的。
-
二进制数的真值与字长
- 真值:就是指二进制数中所有表示值的位数。有符号数的第一位是符号位,那么它的真值就是从第二位开始一直到最后一位。
- 字长:字长是指计算机一次可以处理的二进制的码位长度,是计算机进行数据存储和数据处理的运算单位。如32位处理器,就是指该处理器的字长为32位,一次能处理32位二进制数。通常16位是一个字,32位是一个双字,64位是两个双字。
-
二进制数的四种表现形式
-
原码:人们约定在一个二进制数前用第一位(最高位)来表示符号,即1代表负,0代表正,这就是原码的概念;
-
补码:正数的补码和它的原码相同,而负数的补码则是先把除符号位的其他各位数都取反,再在末位(最低位)加1;
计算机中“模”的概念:
我们把一个计量单位称为模或模数,例如时钟是以12进制进行计数循环的,即模为12。在时钟上,时针加上或减去12的整数倍,时钟的位置都不会发生改变。例如14点在舍去模12后成为下午2点;从时钟0点出发逆时针拨十格即减去10小时,也可以看成从0点出发顺时针拨两格,即2点,因此在模12的前提下,-10可以映射为+2。这样就在计算机中将减法问题转换为加法问题了。10和2对模12互为补数。
-
反码:反码是将除符号位以外的各位都取反得到的进制数,其实反码是原码向补码表现形式转变过程中的一个过渡形式,最终证明它是失败的;
-
移码:移码是一种特殊的二进制数表现形式,它的编码规则如下:正数的符号位为1,负数符号位为0,真值部分与补码相同。因此相求一个数的移码,只需要先求它的补码,再将符号位取反。
-









![[附源码]计算机毕业设计家庭整理服务管理系统Springboot程序](https://img-blog.csdnimg.cn/717d0ef431d74e06b24f75aa820b6b25.png)