图像分割的三大类方法:根据区域间灰度不连续搜寻区域之间的边界,在奇异性检测、边缘连接和边界检测介绍;以像素性质的分布进行阈值处理,在阈值处理介绍;直接搜寻区域进行分割,在基于区域的分割中介绍
奇异性检测
图像局部信息的光滑程度,不光滑的信息有孤立点、线、边缘
点检测
模板:假如模板计算值大于阈值则检测到一个点
−
1
−
1
−
1
−
1
8
−
1
−
1
−
1
−
1
\begin{matrix} -1 & -1 & -1\\ -1 & 8 & -1\\ -1 & -1 & -1 \end{matrix}
−1−1−1−18−1−1−1−1
线检测
模板:假如和某一个模板的响应大于和其他模板的就与该模板对应的方向更加相关
[
−
1
−
1
−
1
2
2
2
−
1
−
1
−
1
]
[
−
1
−
1
2
−
1
2
−
1
2
−
1
−
1
]
[
−
1
2
−
1
−
1
2
−
1
−
1
2
−
1
]
[
2
−
1
−
1
−
1
2
−
1
−
1
−
1
2
]
\left[ \begin{matrix} -1 & -1 & -1 \\ 2 &2&2\\-1&-1&-1 \end{matrix}\right] \left[\begin{matrix} -1&-1&2\\-1&2&-1\\2&-1&-1 \end{matrix}\right] \left[\begin{matrix} -1&2&-1\\-1&2&-1\\-1&2&-1 \end{matrix}\right] \left[\begin{matrix} 2&-1&-1\\-1&2&-1\\-1&-1&2 \end{matrix}\right]
⎣⎡−12−1−12−1−12−1⎦⎤⎣⎡−1−12−12−12−1−1⎦⎤⎣⎡−1−1−1222−1−1−1⎦⎤⎣⎡2−1−1−12−1−1−12⎦⎤
边缘检测
分为理想数字边缘和斜坡数字边缘模型,由黑到白的边缘,一阶导数为正,其他区域导数为0
模板:用差分近似偏导数
基于一阶导数的边缘检测
Roberts算子
1范数衡量幅度
[
1
0
0
−
1
]
[
0
1
−
1
0
]
\left[\begin{matrix} 1&0\\0&-1 \end{matrix}\right] \left[\begin{matrix} 0&1\\-1&0 \end{matrix}\right]
[100−1][0−110]
Sobel算子
无穷范数衡量幅度
[
−
1
0
1
−
2
0
2
−
1
0
1
]
[
1
2
1
0
0
0
−
1
−
2
−
1
]
\left[\begin{matrix} -1&0&1\\-2&0&2\\-1&0&1 \end{matrix}\right] \left[\begin{matrix} 1&2&1\\0&0&0\\-1&-2&-1 \end{matrix}\right]
⎣⎡−1−2−1000121⎦⎤⎣⎡10−120−210−1⎦⎤
Prewitt算子
无穷范数衡量幅度
[
−
1
0
1
−
1
0
1
−
1
0
1
]
[
1
1
1
0
0
0
−
1
−
1
−
1
]
\left[\begin{matrix} -1&0&1\\-1&0&1\\-1&0&1 \end{matrix}\right] \left[\begin{matrix} 1&1&1\\0&0&0\\-1&-1&-1 \end{matrix}\right]
⎣⎡−1−1−1000111⎦⎤⎣⎡10−110−110−1⎦⎤
Canny算子
- 用高斯滤波器平滑图像
- 计算滤波后图像梯度的幅值和方向
- 对梯度幅值应用非极大值抑制,其过程为找出图像梯度中的局部极大值点,把其他非局部极大值点置零以得到细化的边缘;
- 用双阈值算法检测和连续边缘,使用两个阈值T1和T2(T1>T2),T1用来找到每条线段,T2用来在这些线段的两个方向上延伸寻找边缘的断裂处,并连接这些边缘。其中T1代表大于该值的肯定是边缘,T2表示小于该值的肯定不是边缘。
基于二阶导数的边缘检测
拉普拉斯算子
模板:
∇
2
f
=
∂
2
f
∂
x
2
+
∂
2
f
∂
y
2
\nabla^2f=\frac{\partial^2f}{\partial x^2}+ \frac{\partial^2f}{\partial y^2}
∇2f=∂x2∂2f+∂y2∂2f
[
0
1
0
1
−
4
1
0
1
0
]
\left[ \begin{matrix} 0&1&0\\1&-4&1\\0&1&0 \end{matrix} \right]
⎣⎡0101−41010⎦⎤
拉普拉斯-高斯边缘检测算子LOG
先采用高斯函数对图像进行滤波,之后对滤波之后的图像进行拉普拉斯运算,算的值等于0的点是边界点
两种等效计算方法:
- 图像与高斯函数卷积,再求卷积的拉普拉斯微分
- 求高斯函数的拉普拉斯微分,再与图像卷积
边缘连接和边界检测
霍夫变换
在找出边界点集之后,需要连接,形成完整的边界图像描述


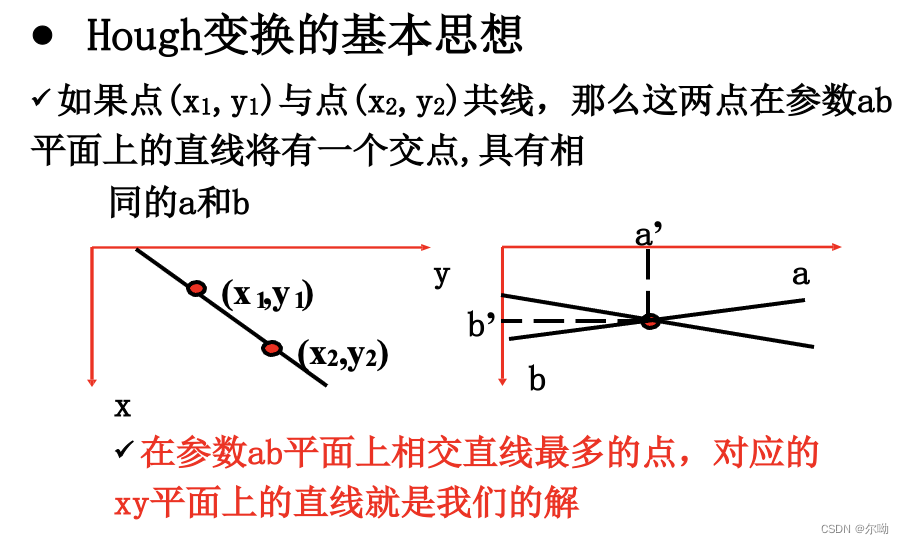
阈值处理
基于灰度统计直方图来切分阈值
T
=
T
[
x
,
y
,
p
(
x
,
y
)
,
f
(
x
,
y
)
]
T = T[x,y,p(x,y),f(x,y)]
T=T[x,y,p(x,y),f(x,y)]
p
(
x
,
y
)
p(x,y)
p(x,y)表示该点的局部性质,
f
(
x
,
y
)
f(x,y)
f(x,y)是该点对应的灰度级
基本全局阈值

基本自适应阈值

最佳全局和自适应阈值
通过边界特性选择阈值
基于不同变量的阈值
区域分割
区域生长的基本概念
区域生长的基本思想是将具有相似属性的像素集合起来构成区域。
具体先对每个需要分割的区域找一个种子像素作为生长的起始点,然后将种子像素周期邻域中与种子像素有相同或相似性质的像素合并到种子像素所在的区域。
将这些新像素当作新的种子像素继续进行上面的过程,直到再没有满足条件的像素。
四叉树分解的分割法
将方形的原始图像分成四个相同大小的方块,判断每个方块是否满足一致性标准;如果满足就不再继续分裂,如果不满足就再细化成四个方块,并对细分得到的方块继续应用一致性经验。
这个迭代重复的过程直到所有的方块都满足一致性标准才停止。
最后,四叉树分解的结果可能包含多种不同尺寸的方块。