503.下一个更大元素II

题目链接：力扣

思路

        与 739. 每日温度 基本相同，其中不同的是，每日温度是一个数组，二这道题目是循环数组，最直接的方法就是将数组展开两倍，然后进行遍历获取结果

        还有就是使用 i % size 来形成循环数组

        假设数组长度为5：
         

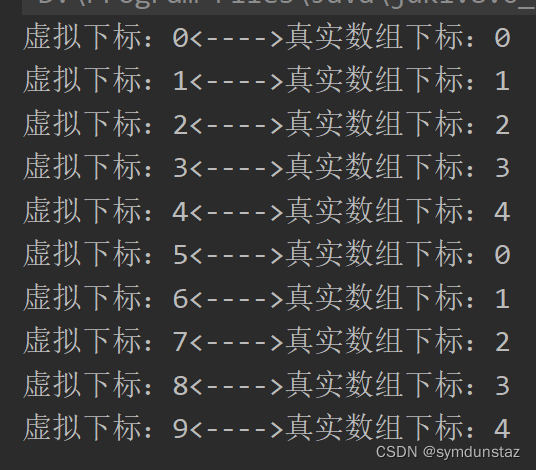
下一个更大元素||

class Solution {
    public int[] nextGreaterElements(int[] nums) {

        // 边界判断
        if (nums == null || nums.length <= 1) {
            return new int[]{-1};
        }

        int size = nums.length;

        // 存放结果
        int[] result = new int[size];
        Arrays.fill(result,-1);

        Stack<Integer> stack = new Stack<>();
        for (int i = 0; i < 2 * size; i++) {
            while (!stack.isEmpty() && nums[i % size] > nums[stack.peek()]) {
                result[stack.peek()] = nums[i % size];
                stack.pop();
            }
            stack.push(i % size);
        }

        return result;
    }
}

42. 接雨水

题目链接：力扣

思路

        这道题目很经典，彻底弄明白确实很费劲，有很多方法可以做

双指针法

• 一列一列来进行计算，这样每一列的宽度就是固定的，都是 1，只需要求出每一列的高度就可以了
• 高度怎么求：每一列雨水的高度，取决于，该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度
• 从头遍历一遍所有的列，然后求出每一列雨水的体积，相加之后就是总雨水的体积了

动态规划

• 双指针法是有重复计算的，每次都会重新计算当前下标的左右最高
• 可以使用动态规划一次性先将每一个下标的左右最高存放在两个节点中，再去计算其告诉就不用每次都重复计算了

单调栈

• 这个方法不好理解，暂时还没有理解好，二刷再攻克吧

接雨水

双指针法

class Solution {
    public int trap(int[] height) {
        int sum = 0;
        for (int i = 0; i < height.length; i++) {
            
            // 第一个柱子和最后一个柱子不接雨水
            if (i==0 || i== height.length - 1) continue;
            
            int rHeight = height[i]; // 记录右边柱子的最高高度
            int lHeight = height[i]; // 记录左边柱子的最高高度
            for (int r = i+1; r < height.length; r++) {
                if (height[r] > rHeight) rHeight = height[r];
            }
            for (int l = i-1; l >= 0; l--) {
                if(height[l] > lHeight) lHeight = height[l];
            }
            int h = Math.min(lHeight, rHeight) - height[i];
            if (h > 0) sum += h;
        }
        return sum;

    }
}

动态规划

class Solution {
    public int trap(int[] height) {
        int length = height.length;
        if (length <= 2) return 0;
        int[] maxLeft = new int[length];
        int[] maxRight = new int[length];
        
        // 记录每个柱子左边柱子最大高度
        maxLeft[0] = height[0];
        for (int i = 1; i< length; i++) maxLeft[i] = Math.max(height[i], maxLeft[i-1]);
        
        // 记录每个柱子右边柱子最大高度
        maxRight[length - 1] = height[length - 1];
        for(int i = length - 2; i >= 0; i--) maxRight[i] = Math.max(height[i], maxRight[i+1]);
        
        // 求和
        int sum = 0;
        for (int i = 0; i < length; i++) {
            int count = Math.min(maxLeft[i], maxRight[i]) - height[i];
            if (count > 0) sum += count;
        }
        return sum;
    }
}

单调栈

class Solution {
    public int trap(int[] height){
        int size = height.length;

        if (size <= 2) return 0;

        Stack<Integer> stack = new Stack<Integer>();
        stack.push(0);

        int sum = 0;
        for (int index = 1; index < size; index++){
            int stackTop = stack.peek();
            if (height[index] < height[stackTop]){
                stack.push(index);
            }else if (height[index] == height[stackTop]){
                
                stack.pop();
                stack.push(index);
            }else{
                //pop up all lower value
                int heightAtIdx = height[index];
                while (!stack.isEmpty() && (heightAtIdx > height[stackTop])){
                    int mid = stack.pop();
                    
                    if (!stack.isEmpty()){
                        int left = stack.peek();

                        int h = Math.min(height[left], height[index]) - height[mid];
                        int w = index - left - 1;
                        int hold = h * w;
                        if (hold > 0) sum += hold;
                        stackTop = stack.peek();
                    }
                }
                stack.push(index);
            }
        }
        
        return sum;
    }
}

84.柱状图中最大的矩形

题目链接：力扣

思路

        和接雨水比较一致，原理上都是很相似的

柱状图最大的矩形

动态规划

class Solution {
    public int largestRectangleArea(int[] heights) {
        int length = heights.length;
        int[] minLeftIndex = new int [length];
        int[] minRightIndex = new int [length];
        // 记录左边第一个小于该柱子的下标
        minLeftIndex[0] = -1 ;
        for (int i = 1; i < length; i++) {
            int t = i - 1;
            // 这里不是用if，而是不断向右寻找的过程
            while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
            minLeftIndex[i] = t;
        }
        // 记录每个柱子右边第一个小于该柱子的下标
        minRightIndex[length - 1] = length;
        for (int i = length - 2; i >= 0; i--) {
            int t = i + 1;
            while(t < length && heights[t] >= heights[i]) t = minRightIndex[t];
            minRightIndex[i] = t;
        }
        // 求和
        int result = 0;
        for (int i = 0; i < length; i++) {
            int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
            result = Math.max(sum, result);
        }
        return result;
    }
}

单调栈

class Solution {
    int largestRectangleArea(int[] heights) {
        Stack<Integer> st = new Stack<Integer>();
        
        int [] newHeights = new int[heights.length + 2];
        newHeights[0] = 0;
        newHeights[newHeights.length - 1] = 0;
        for (int index = 0; index < heights.length; index++){
            newHeights[index + 1] = heights[index];
        }

        heights = newHeights;
        
        st.push(0);
        int result = 0;
      
        for (int i = 1; i < heights.length; i++) {
            
            if (heights[i] > heights[st.peek()]) {
                st.push(i);
            } else if (heights[i] == heights[st.peek()]) {
                st.pop();
                st.push(i);
            } else {
                while (heights[i] < heights[st.peek()]) { 
                    int mid = st.peek();
                    st.pop();
                    int left = st.peek();
                    int right = i;
                    int w = right - left - 1;
                    int h = heights[mid];
                    result = Math.max(result, w * h);
                }
                st.push(i);
            }
        }
        return result;
    }
}