最短路算法总览
Dijkstra算法
- 1.朴素Dijkstra算法
- - 算法步骤
  - 算法应用
  - - Dijkstra求最短路Ⅰ
- 2.堆优化Dijkstra算法
- - 算法步骤
  - 算法应用
  - - Dijkstra求最短路Ⅱ
Bellman-Ford算法
- 算法步骤
- 算法应用
- - 有边数限制的最短路
SPFA算法
- 算法步骤
- 算法应用
- - 1. spfa求最短路
  - 2. spfa判断负环
Floyd算法
- 算法步骤
- 算法应用
- - floyd求最短路

最短路算法总览

使用概括

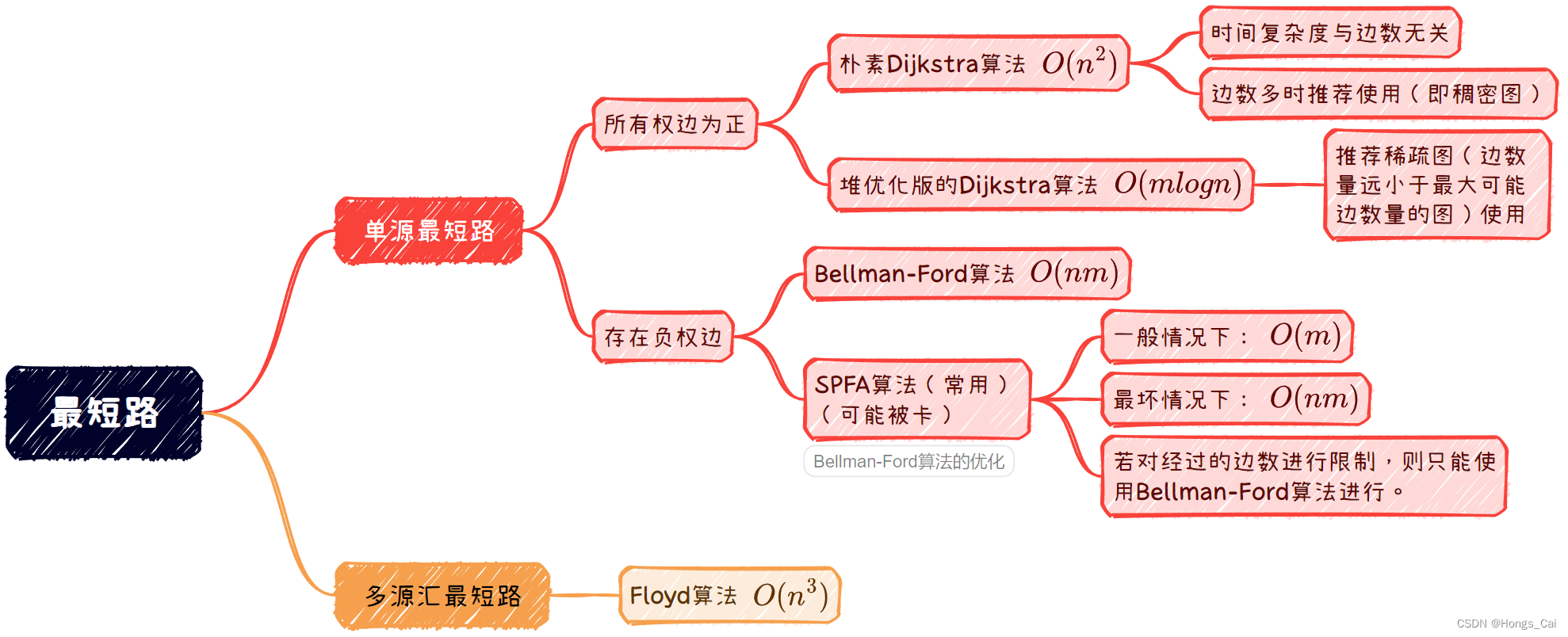
Dijkstra算法

1.朴素Dijkstra算法

算法步骤

朴素Dijkstra算法的主要步骤如下：

①初始时，标记所有节点为未访问。设源点s的距离为0，其他点的距离为正无穷。
②从未访问的节点中选择距离最短的节点u，标记u为已访问。
③对于u的所有未访问邻接点v，更新dist[v] = min(dist[v], dist[u] + w(u,v))。其中w(u,v)是边(u,v)的长度，dist[]存储各点当前的最短距离。
④重复步骤2和3，直到所有可达节点都被标记为已访问。
⑤计算结束，dist[]数组中存储了源点到其他所有点的最短路径长度。

注意：每次迭代的过程中，都先找到当前未确定的最短距离的点中距离最短的点。

时间复杂度： $O(n^2)$

算法应用

Dijkstra求最短路Ⅰ

题目描述：
给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 $1$ 号点到 $n$ 号点的最短距离，如果无法从 $1$ 号点走到 $n$ 号点，则输出 −1。

输入格式：
第一行包含整数 $n$ 和 $m$ 。

接下来 $m$ 行每行包含三个整数 $x ， y ， z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。

输出格式：
输出一个整数，表示 $1$ 号点到 $n$ 号点的最短距离。

如果路径不存在，则输出 −1。

数据范围：
$1≤n≤500，1≤m≤10^5$ ，图中涉及边长均不超过 $10000$ 。

输入样例：

输出样例：

代码实现：

#define _CRT_SECURE_NO_WARNINGS

#include<iostream>
#include<cstring>

using namespace std;

const int N = 510;
int g[N][N], d[N], n, m; // 用于存储每个点到起点的最短距离
bool st[N]; // 用于在更新最短距离时 判断当前的点的最短距离是否确定 是否需要更新
    
int Dijkstra()
{
	memset(d, 0x3f, sizeof d); // 初始化为无穷大
	d[1] = 0;
	for (int i = 0; i < n; ++i)
	{
		int t = -1;
		for (int j = 1; j <= n; ++j)
		{
			if (!st[j] && (t == -1 || d[t] > d[j])) // 寻找还未确定最短路的点中路径最短的点
				t = j;
		}

		st[t] = true;

		for (int j = 1; j <= n; ++j)
			d[j] = min(d[j], d[t] + g[t][j]);
	}
	return d[n] == 0x3f3f3f3f ? -1 : d[n];
}
int main()
{
	cin.tie(0);
	ios::sync_with_stdio(false);
	memset(g, 0x3f, sizeof g);
	cin >> n >> m;
	while (m--)
	{
		int a, b, c;
		cin >> a >> b >> c;
		g[a][b] = min(g[a][b], c); // 防止重边，取最短的一条路径
	}
	cout << Dijkstra() << endl;
	return 0;
}

2.堆优化Dijkstra算法

算法步骤

对于给定的图G = (V,E)和源节点s，Dijkstra算法寻找从s到达所有其他节点v的最短路径。堆优化Dijkstra算法主要步骤如下:

①创建节点集合S，初始为空。创建优先级队列Q，将源节点s的距离dist[s]设为0，其他节点设为无穷大，并按距离插入Q。
②当Q非空时，取出Q中dist最小的节点u。
③对u的所有出边(u,v)，检查dist[u] + w(u,v) < dist[v]是否成立。如果成立,则使用dist[u] + w(u,v)更新dist[v]，并更新v在Q中的位置。
④将u加入S。
⑤重复步骤②-④，直到Q为空。

时间复杂度：
如果使用的是手动实现的堆，可以维持堆在 n 个元素，其整体时间复杂度为 $O (m l o g n)$ ， $O (l o g n)$ 为每回上下调整堆所需的时间复杂度。

如果使用的是STL容器提供的优先队列，只可维持堆在m个元素，其整体时间复杂度为 $O (m l o g m)$ ，但 $m$ $\leq$ $n^2$ ，可得 $l o g m$ $\leq$ $logn^2$ （即 $l o g m$ $\leq$ $2 l o g n$ ），与手动实现的堆还是处于同一级别。

算法应用

Dijkstra求最短路Ⅱ

题目描述：
给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 $1$ 号点到 $n$ 号点的最短距离，如果无法从 $1$ 号点走到 $n$ 号点，则输出 −1。

输入格式：
第一行包含整数 $n$ 和 $m$ 。

接下来 $m$ 行每行包含三个整数 $x, y, z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。

输出格式：
输出一个整数，表示 $1$ 号点到 $n$ 号点的最短距离。

如果路径不存在，则输出 −1。

数据范围：
$1≤n,m≤10^5$ ，图中涉及边长均不小于 $0$ ，且不超过 $10000$ 。
数据保证：如果最短路存在，则最短路的长度不超过 $10^9$ 。

输入样例：

输出样例：

代码实现：

#define _CRT_SECURE_NO_WARNINGS

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1.5e5 + 10;
int h[N], e[N], ne[N], w[N], idx;
int dist[N];
bool st[N];
int n, m;
typedef pair<int, int> PII;

void add(int a, int b, int c)
{
	e[idx] = b;
	w[idx] = c;
	ne[idx] = h[a];
	h[a] = idx++;
}
int Dijkstra()
{
	priority_queue<PII, vector<PII>, greater<PII>> heap;
	memset(dist, 0x3f, sizeof dist);
	dist[1] = 0;
	heap.push({0, 1});
	while (heap.size())
	{
		auto t = heap.top();
		heap.pop();
		int u = t.second, distance = t.first;
		if (st[u]) continue;
		st[u] = true;
		for (int i = h[u]; i != -1; i = ne[i])
		{
			int j = e[i];
			if (dist[j] > dist[u] + w[i])
			{
				dist[j] = dist[u] + w[i];
				heap.push({ dist[j], j });
			}
		}
	}
	return dist[n] == 0x3f3f3f3f ? -1 : dist[n];
}
int main()
{
	cin.tie(0);
	ios::sync_with_stdio(false);
	memset(h, -1, sizeof h);
	cin >> n >> m;
	for (int i = 1; i <= m; ++i)
	{
		int x, y, z;
		cin >> x >> y >> z;
		add(x, y, z);
	}
	cout << Dijkstra() << endl;
	return 0;
}

Bellman-Ford算法

算法步骤

Bellman-Ford算法步骤如下：

①创建一个距离数组dist，用于存储从源节点到每个节点的最短距离。将源节点的距离设为0，其他节点的距离设为无穷大。

②进行V-1轮松弛操作：对所有节点进行V-1轮松弛操作，其中V是图中节点的数量。在每一轮松弛中，遍历图中的所有边，尝试通过当前节点u到达其相邻节点v的距离是否比当前最短距离更短，如果是，则更新节点v的最短距离为distance[u] + weight(u, v)。

③检查负权环：进行第V轮松弛操作后，再进行一次遍历，检查是否还存在通过松弛操作使得节点的距离进一步减小的情况。如果存在这样的情况，则说明图中存在负权环，因为负权环可以无限次地降低路径长度，这时Bellman-Ford算法会返回一个错误的结果。

④返回结果：如果不存在负权环，最终的距离数组dist就是从源节点到其他节点的最短距离。

tip：

负权环：
负权环是指在一个环中，所有边的权重之和为负值。由于负权环的存在，路径长度可以无限地减小，因此Bellman-Ford算法不适用于含有负权环的图。

在最短路存在的前提下，那么我们每一次的松弛操作都应当让最短路的边数 +1，而最短路最多只有 $n - 1$ 条边，故最多循环 $n - 1$ 次，即可得出结果，而每次对边进行松弛时间复杂度是 $O (m)$ ，故总时间复杂度是 $O (nm)$ 。

Bellman−Ford算法还可以检测图中是否存在负权环，当循环松弛操作n−1次后，第n次操作仍然有边发生了松弛操作，那么就意味着n个点的最短路可以拥有n条边，因此必然存在环，但一般判断负环不使用Bellman−Ford算法，而是用优化后的版本SPFA算法，包括求最短路也是，那么Bellman−Ford算法还有什么优势呢？优势就在于本题，有边数限制的最短路问题只能用Bellman−Ford算法来求解。

注意：
①每次松弛的时候，使用的是上次松弛完的结果来计算本次的结果，因此计算的时候需要备份一次上次的结果，以免发生“串联更新”的问题，也就是使用本次松弛计算的结果来更新后续的结果；

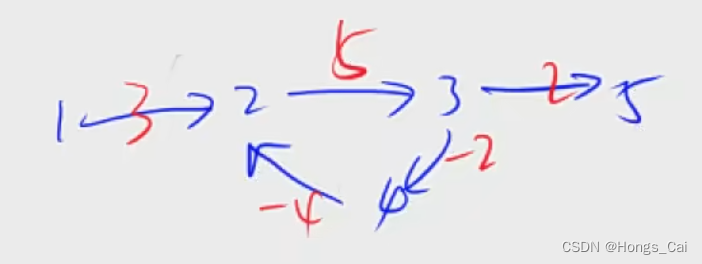
②输出答案时，可能存在负权边更新了两个无法到达的点的情况，所以判断不能直接判断是否等于 0x3f3f3f3f，比如1无法到达点5，也无法到达点7，但 5->7 的边权是 -2，那么在每次松弛的时候，是会导致这个值变小一点点的。

算法应用

有边数限制的最短路

题目描述：
给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，边权可能为负数。

请你求出从 $1$ 号点到 $n$ 号点的最多经过 $k$ 条边的最短距离，如果无法从 $1$ 号点走到 $n$ 号点，输出 impossible。

注意：图中可能存在负权回路。

输入格式：
第一行包含三个整数 $n, m, k$ 。

接下来 $m$ 行，每行包含三个整数 $x, y, z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。

点的编号为 $1 \sim n$ 。

输出格式：
输出一个整数，表示从 $1$ 号点到 $n$ 号点的最多经过 $k$ 条边的最短距离。

如果不存在满足条件的路径，则输出 impossible。

数据范围：
$1 \leq n, k \leq 500, 1 \leq m \leq 10000, 1 \leq x, y \leq n$ ，任意边长的绝对值不超过 $10000$ 。

输入样例：

输出样例：

代码实现：
1.采用结构体来储存边的信息

// 这行代码禁用了与使用某些标准库函数相关的警告。
#define _CRT_SECURE_NO_WARNINGS

#include<iostream>
#include<cstring>
using namespace std;

const int N = 510, M = 10010;
int n, m, k;
int dist[N], backup[N];
struct Edge
{
	int a, b, c;
} edges[M];

// 使用 Bellman-Ford 算法实现从节点 1 到节点 n 的最短路径查找。
void bellman_ford()
{
	// 使用一个大值（0x3f3f3f3f）初始化距离数组作为初始距离估计。
	// 0x3f3f3f3f 表示一个非常大的值，在此上下文中被视为无穷大。
	memset(dist, 0x3f, sizeof dist);
	dist[1] = 0; // 节点 1 到自身的距离为 0。

	// 运行 Bellman-Ford 算法 'k' 次迭代。
	for (int i = 0; i < k; ++i)
	{
		// 备份上一次迭代的距离数组，以便在本次迭代中使用，防止发生串联。
		memcpy(backup, dist, sizeof dist);

		// 对每一条边进行松弛操作。
		for (int j = 0; j < m; ++j)
		{
			auto e = edges[j];
			dist[e.b] = min(dist[e.b], backup[e.a] + e.c);
		}
	}
}

int main()
{
	cin.tie(0);
	ios::sync_with_stdio(false);

	cin >> n >> m >> k; // 输入节点数、边数和迭代次数。
	for (int i = 0; i < m; ++i)
	{
		int a, b, c;
		cin >> a >> b >> c;
		edges[i] = { a, b, c }; // 输入每条边的起点、终点和权值，保存在 edges 数组中。
	}

	bellman_ford(); // 运行 Bellman-Ford 算法找到从节点 1 到节点 n 的最短路径。

	// 如果最终的距离值大于 0x3f3f3f3f 的一半，则输出 "impossible"，表示无法到达节点 n。
	// 否则，输出最终的距离值，表示从节点 1 到节点 n 的最短路径长度。
	if (dist[n] > 0x3f3f3f3f / 2)
		cout << "impossible";
	else
		cout << dist[n];

	return 0;
}

2.采用邻接表来储存边的信息

#define _CRT_SECURE_NO_WARNINGS #include<iostream> #include<cstring> using namespace std; const int N = 510, M = 10010; int n, m, k; int h[N], e[N], ne[N], w[N], idx; int dist[N], backup[N]; void add(int a, int b, int c) { e[idx] = b; w[idx] = c; ne[idx] = h[a]; h[a] = idx++; } void bellman_ford() { memset(dist, 0x3f, sizeof dist); dist[1] = 0; for (int i = 0; i < k; ++i) // 重复k次松弛操作 { memcpy(backup, dist, sizeof dist); // 备份上一轮的距离数组，防止出现串联现象 for (int j = 1; j <= n; ++j) { for (int t = h[j]; t != -1; t = ne[t]) { int u = e[t]; dist[u] = min(dist[u], w[t] + backup[j]); // 松弛操作 } } } } int main() { cin.tie(0); ios::sync_with_stdio(false); memset(h, -1, sizeof h); cin >> n >> m >> k; for (int i = 0; i < m; ++i) { int a, b, c; cin >> a >> b >> c; add(a, b, c); } bellman_ford(); // 因为有负权边所以可能出现d[n]比0x3f3f3f3f稍微小一些 if (dist[n] > 0x3f3f3f3f / 2) cout << "impossible" << endl; else cout << dist[n]; return 0; }

SPFA算法

SPFA算法是解决单源最短路径问题的一种算法，全称为Shortest Path Faster Algorithm。它是Bellman-Ford算法的一种改进版本，主要思想是利用队列进行松弛操作，避免重复松弛已确定最短路径的节点，从而提高效率。

算法步骤

SPFA算法的步骤如下:

初始时,源点s的距离dist[s]为0,其他顶点的距离为正无穷。使用一个队列queue存储待优化的顶点。一开始只有源点s入队。
当队列不空时,重复以下操作:
(1) 出队顶点u。
(2) 对u的所有出边顶点v,如果dist[u] + weight(u,v) < dist[v],则进行松弛操作:

dist[v] = dist[u] + weight(u,v) // 如果v不在队列中,则入队v。

直到队列为空,算法结束。此时dist数组存储了源点到其他所有顶点的最短距离。

SPFA算法与Dijkstra算法类似，但通过队列实现了动态松弛，对于稠密图或存在负权边的图会更加高效。需要注意的是，SPFA存在罕见的指数时间复杂度的情况,因此不如Dijkstra算法稳定。但对绝大多数图而言，SPFA仍然是一种高效解决单源最短路径问题的算法。

算法应用

1. spfa求最短路

题目描述：
给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，边权可能为负数。

请你求出 $1$ 号点到 $n$ 号点的最短距离，如果无法从 $1$ 号点走到 $n$ 号点，则输出 impossible。

数据保证不存在负权回路。

输入格式：
第一行包含整数 $n$ 和 $m$ 。

接下来 $m$ 行每行包含三个整数 $x, y, z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。

输出格式：
输出一个整数，表示 $1$ 号点到 $n$ 号点的最短距离。

如果路径不存在，则输出 impossible。

数据范围：
$1≤n,m≤10^5$ ，图中涉及边长绝对值均不超过 $10000$ 。

输入样例：

3 3 1 2 5 2 3 -3 1 3 4

输出样例：

2

代码实现：

#define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <cstring> #include <queue> using namespace std; const int N = 1e5 + 10; // 最大节点数 int h[N], e[N], ne[N], w[N], idx; // 图的邻接表表示所需的数组 int dist[N], n, m; // 存储每个节点到节点1的最短距离的数组，以及节点数和边数的变量 bool st[N]; // 用于记录节点是否在松弛队列中的数组 // 添加一条边到图中 void add(int a, int b, int c) { e[idx] = b; // 边的目标节点 ne[idx] = h[a]; // 节点a在邻接表中的下一条边 w[idx] = c; // 边的权重/代价 h[a] = idx++; // 将边添加到节点a的邻接表中 } // 最短路径快速算法（SPFA）用于找到从节点1到所有其他节点的最短路径 void spfa() { queue<int> q; memset(dist, 0x3f, sizeof dist); // 将所有节点的最短距离初始化为无穷大 dist[1] = 0; // 节点1到自身的距离为0 st[1] = true; // 将节点1加入松弛队列 q.push(1); // 将节点1加入队列 while (q.size()) { auto t = q.front(); q.pop(); st[t] = false; // 将节点t从松弛队列中移出 for (int i = h[t]; i != -1; i = ne[i]) { int j = e[i]; if (dist[j] > dist[t] + w[i]) { dist[j] = dist[t] + w[i]; // 通过节点t进行松弛 if (st[j]) continue; // 如果节点j已经在松弛队列中，跳过本次循环 st[j] = true; // 将节点j加入松弛队列 q.push(j); // 将节点j加入队列 } } } } int main() { cin.tie(0); ios::sync_with_stdio(false); memset(h, -1, sizeof h); // 初始化邻接表为空 cin >> n >> m; // 输入节点数和边数 for (int i = 0; i < m; ++i) { int a, b, c; cin >> a >> b >> c; // 输入边的起点、终点和权重 add(a, b, c); // 将边添加到图中 } spfa(); // 运行SPFA算法 if (dist[n] == 0x3f3f3f3f) cout << "impossible" << endl; // 如果节点n的最短距离仍然是无穷大，则说明节点n不可达 else cout << dist[n] << endl; // 输出从节点1到节点n的最短距离 return 0; }

tip：
关于st数组的解释：队列中有重复的点没有意义,因为前面假如出现了可以把二这个点变小的值，那就更新，但不用加入队列，因为队列里已经有二这个点了，他肯定会遍历到，然后去更新与他相邻的节点之间的距离，这样就提高了效率，而被淘汰的点之后又会被加入队列是因为此时他的最短距离又被更新了，那么自然和他相连的节点距离也会更新，所以需要把他重新加入队列之中。

2. spfa判断负环

题目描述：
给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，边权可能为负数。

请你判断图中是否存在负权回路。

输入格式：
第一行包含整数 $n$ 和 $m$ 。

接下来 $m$ 行每行包含三个整数 $x, y, z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。

输出格式：
如果图中存在负权回路，则输出 Yes，否则输出 No。

数据范围：
$1 \leq n \leq 2000, 1 \leq m \leq 10000$ ，图中涉及边长绝对值均不超过 $10000$ 。

输入样例：

3 3 1 2 -1 2 3 4 3 1 -4

输出样例：

Yes

代码实现：

#define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <cstring> #include <queue> using namespace std; const int N = 2e3 + 10, M = 1e4 + 10; int h[N], e[M], ne[M], w[M], idx; int n, m; int dist[N], cnt[N]; bool st[N]; // 添加一条从节点a到节点b的有向边，权值为c void add(int a, int b, int c) { e[idx] = b; w[idx] = c; ne[idx] = h[a]; h[a] = idx++; } // 使用SPFA算法判断图中是否存在负环 bool spfa() { // 仅检测负环，不用初始化dist数组 queue<int> q; // 构建超级源点，防止负环与出发点不连通 for (int i = 1; i <= n; ++i) q.push(i); // 将所有节点加入队列 while (q.size()) { auto t = q.front(); q.pop(); st[t] = false; // 标记节点t不在队列中 for (int i = h[t]; i != -1; i = ne[i]) { int j = e[i]; // 遍历节点t的所有出边 if (dist[j] > dist[t] + w[i]) { dist[j] = dist[t] + w[i]; // 更新节点j的最短距离 cnt[j] = cnt[t] + 1; // 更新节点j经过的边数 if (cnt[j] >= n) return true; // 如果节点j经过的边数超过n（图中节点个数），说明存在负环 if (st[j]) continue; // 如果节点j已经在队列中，直接跳过 st[j] = true; // 将节点j标记为在队列中 q.push(j); // 将节点j加入队列 } } } return false; // 图中不存在负环 } int main() { cin.tie(0); ios::sync_with_stdio(false); memset(h, -1, sizeof h); // 初始化邻接表头节点为-1，表示空链表 cin >> n >> m; for (int i = 0; i < m; ++i) { int a, b, c; cin >> a >> b >> c; add(a, b, c); // 添加一条从节点a到节点b的有向边，权值为c } if (spfa()) cout << "Yes" << endl; // 存在负环，输出"Yes" else cout << "No" << endl; // 不存在负环，输出"No" return 0; }

注意：

1. 为什么把所有点入队？

可以假设一个虚拟源点0点，从虚拟源点连一条权值是0的边到所有点，这样这个新图其实是和原图等价的（原图上有负环等价于新图上有负环），做 spfa 的时候首先把 0 入队，第一次迭代的时候会把0出队，然后把和 0 点相连的点全部入队，那么就相当于把 n - 1 的所有点入队，而如果直接把所有点入队，效果也是一样的，相当于自己手动迭代了一次spfa。

2. dist数组为什么初始化为什么值都无所谓？

dist数组的初始值肯定是一个有限值，一个有限值每次减一个有限值（负环上跑一次），然后减无限次，最终 dist[] 减成 -INF。即 dist[] 初值是多少都无所谓，因为会减无限次有限值，你再大的数减无限次有限值肯定减成 -INF。我们只要用抽屉原理保证迭代超过 n 次的时候，说明路径上有起码 n+1 个点，说明有重复点，即有负环就行。

Floyd算法

基本介绍：
Floyd算法，也被称为Floyd-Warshall算法，用于解决任意两点之间的最短路径问题，包括带权图中的最短路径问题。该算法采用动态规划的思想，可以处理有向图或带负权边的图，但不能处理含有负权回路的图。

基本原理：
$f [k] [i] [j]$ 表示从节点 $i$ 到节点 $j$ 经过编号为 $1.. k$ 的节点的最短路径长度。
初值 $f [0] [i] [j]$ 是原图的邻接矩阵，表示直接相连的节点之间的距离。
然后，我们用递推的方式计算 $f [k] [i] [j]$ ：

从节点 $i$ 到节点 $j$ 不经过节点 $k$ ： $f [k] [i] [j]$ 可以从 $f [k - 1] [i] [j]$ 转移过来，也就是没有经过节点 $k$ 的情况下的最短路径。
从节点 i 到节点 j 经过节点 k： $f [k] [i] [j]$ 可以从 $f [k - 1] [i] [k] 和 f [k - 1] [k] [j]$ 两个部分转移过来，意味着我们将路径拆分成 $i$ 到 $k$ 和 $k$ 到 $j$ ，然后再加在一起。
转移方程为： $f [k] [i] [j] = min (f [k - 1] [i] [j], f [k - 1] [i] [k] + f [k - 1] [k] [j])$

通过不断迭代 $k$ 的值，我们最终可以得到 $f [k] [i] [j]$ ，其中 $k$ 的范围是从 $1$ 到节点数量。

Floyd可以处理负权边，但不能处理负权回路。

算法步骤

Floyd算法的步骤：

初始化：

创建一个二维数组dist，用于存储任意两点之间的最短距离。dist[i][j]表示顶点i到顶点j的最短距离。
将dist[i][j]初始化为正无穷，表示初始状态下没有直接边相连，即没有路径。
对角线元素dist[i][i]初始化为0，表示到自身的距离为0。
根据图的边信息，将直接相连的两个顶点之间的距离填入dist数组。

更新最短路径：

对于每个顶点k，考虑所有可能的顶点对(i, j)的最短距离。
如果从顶点i经过顶点k到达顶点j的路径距离比当前的dist[i][j]更短，则更新dist[i][j]为更短的距离。

递推更新：

重复进行第2步，直到每个顶点都被当作中间顶点考虑过为止。

得到结果：

最终，dist数组中的元素即为任意两点之间的最短路径距离。

算法应用

floyd求最短路

题目描述：
给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，边权可能为负数。

再给定 $k$ 个询问，每个询问包含两个整数 $x$ 和 $y$ ，表示查询从点 $x$ 到点 $y$ 的最短距离，如果路径不存在，则输出 impossible。

数据保证图中不存在负权回路。

输入格式：
第一行包含三个整数 $n, m, k$ 。

接下来 $m$ 行，每行包含三个整数 $x, y, z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。

接下来 $k$ 行，每行包含两个整数 $x, y$ ，表示询问点 $x$ 到点 $y$ 的最短距离。

输出格式：
共 $k$ 行，每行输出一个整数，表示询问的结果，若询问两点间不存在路径，则输出 impossible。

数据范围：
$1≤n≤200,1≤k≤n^2,1≤m≤20000$ ，图中涉及边长绝对值均不超过 $10000$ 。

输入样例：

3 3 2 1 2 1 2 3 2 1 3 1 2 1 1 3

输出样例：

impossible 1

代码实现：

#define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <cstring> using namespace std; const int N = 210, M = 2e4 + 10; int d[N][N]; // 用于存储节点之间的最短距离的二维数组 int n, m, k; // 变量n表示节点数，m表示边数，k表示查询数 // 使用Floyd-Warshall算法计算所有节点对之间的最短路径 void floyd() { for (int k = 1; k <= n; ++k) // 中间节点遍历循环 { for (int i = 1; i <= n; i++) // 源节点遍历循环 { for (int j = 1; j <= n; j++) // 目标节点遍历循环 { // 更新经过节点i和j的最短路径，其中中间节点为k d[i][j] = min(d[i][j], d[i][k] + d[k][j]); } } } } int main() { cin.tie(0); ios::sync_with_stdio(false); cin >> n >> m >> k; memset(d, 0x3f, sizeof d); // 初始化所有节点之间的距离为无穷大 for (int i = 0; i < n; i++) d[i][i] = 0; // 节点自身到自身的距离为0 while (m--) { int a, b, c; cin >> a >> b >> c; d[a][b] = min(d[a][b], c); // 更新节点a和节点b之间的距离为c的最小值 } floyd(); // 计算所有节点对之间的最短路径 while (k--) { int a, b; cin >> a >> b; if (d[a][b] > 0x3f3f3f3f / 2) cout << "impossible" << endl; // 输出无穷大表示不可达 else cout << d[a][b] << endl; // 输出节点a到节点b的最短距离 } return 0; }