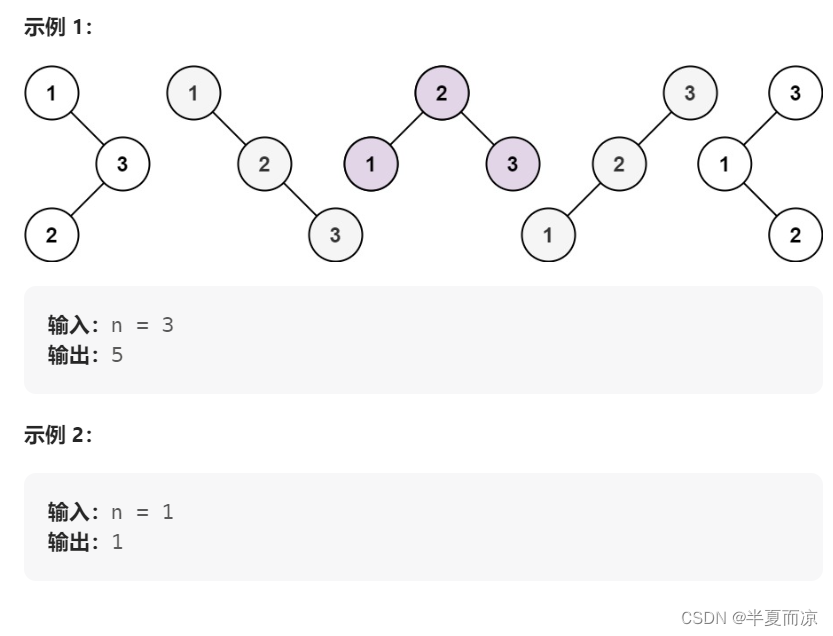
216. 组合总和 III


这道题和昨天的相似的地方,但是也有不同的特点。这道题规定了数字范围是从1-9,并且一个组合中,不能出现同样的元素,比如说[1,2,2]这个就不可以,如果取过2之后,就只能往后找。
这就导致这里会比昨天多一个剪枝的操作。如果当前的path已经达到了k的长度,但是不满足和等于n,那么就pop出来并且减掉当前的元素。如果当前既满足长度,也满足和相等,那么就加入到我们的答案数组中。
递归三部曲:
终止条件:当path的长度满足k并且和等于n的时候,加入到答案数组中
递归参数:n代表目标和,k代表path长度,start代表下一层循环从第哪个元素开始,还有一个target_sum代表当前元素总和
单层递归逻辑:对于每一个元素进行相加,用target_sum储存直到满足长度k为止,如果不满足那么就pop并减掉当前元素然后从下一个元素开始
代码:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
path = []
result = []
def backtracking(sum_num,k,start,n):
if len(path)==k:
if sum_num==n:
result.append(path[:])
return
for i in range(start,10):
sum_num +=i
path.append(i)
backtracking(sum_num,k,i+1,n)
path.pop()
sum_num-=i
backtracking(0,k,1,n)
return result
Leetcode17电话号码的字母组合
17. 电话号码的字母组合 - 力扣(Leetcode)
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。


最最最最暴力的方法,for循环嵌套。或者直接用python的内置函数iteral.product求笛卡尔乘积,学过sql的朋友应该不陌生,这道题就是类似sql的join然后求笛卡尔乘积
但是我们开始了回溯算法的章节,那么肯定要用回溯来写!
思路:首先需要创一个哈希表,数字和他所映射的字母 一 一 对应
然后依旧是转化为树形结构来看,如下图!
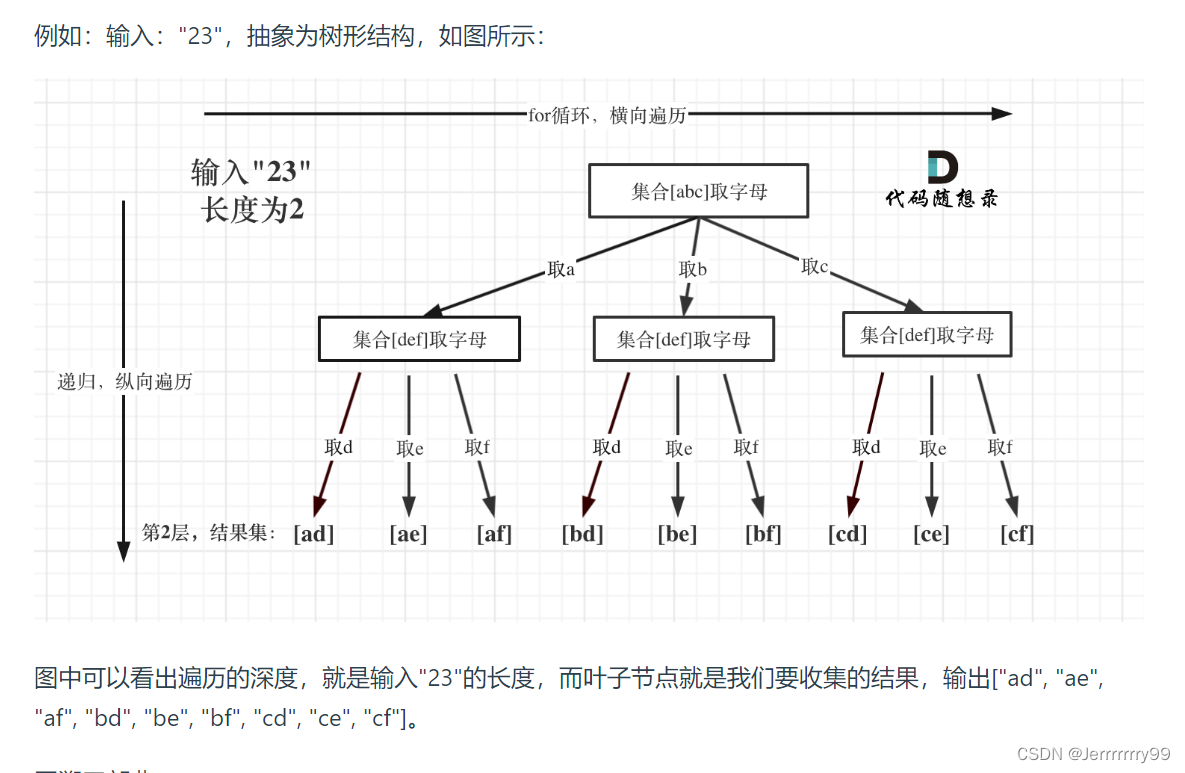
树的深度就是当前digits的长度,而最后的叶子节点就是我们要收集的结果,那么回溯出现在哪里呢?是不是最后一层找完了我们要继续回到上一层去找。
递归三部曲:
终止条件:如果index==len(digits),index就代表当前遍历的位置,如果index等于了当前digits的长度,那么就加入结果集并return
递归参数:首先需要一个字符串s来收集叶子节点的结果,然后用一个字符串数组result保存。也就是:s,digits,index
单层循环逻辑:首先找到当前要遍历digits中字母的位置,也就是map[digits[index]],index从0开始,获取到了第一个数字 然后再map中找到了这个数字映射的字母
for循环对这个数字指向的字母,s+=i,因为s是字符串哈!我们最后传入的时候是一个" ".
然后开始递归下一层,这里递归了之后是需要返回到上一层的,也就是s = s[:-1],这个就代表我们回溯到上一层的字母。然后继续遍历其他的字母。
这里递归我讲一下,主要是熟悉这个思路,至于递归里面的过程真的没有必要去扣出来,因为一不小心就会绕进去然后出不来,虽然我每次都被绕进去。。。。。
代码:
def letterCombinations(self, digits: str) -> List[str]:
result = []
def backtrace(digits,index,s:str):
map ={ '2':'abc',
'3':'def',
'4':'ghi',
'5':'jkl',
'6':'mno',
'7':'pqrs',
'8':'tuv',
'9':'wxyz'}
if not digits:
return []
if index==len(digits):
result.append(s)
return
letters = map[digits[index]]
for letter in letters:
s+=letter
backtrace(digits,index+1,s)
s=s[:-1]
backtrace(digits,0,'')
return result