Leetcode 动态规划详解

动态规划（Dynamic Programming, DP）是一种解决多阶段决策过程最优化问题的数学方法。动态规划的特点是将原问题分解成多个子问题进行求解，每个子问题只求解一次，并将其结果保存下来，避免重复计算。然后通过组合子问题的解来得到原问题的解。

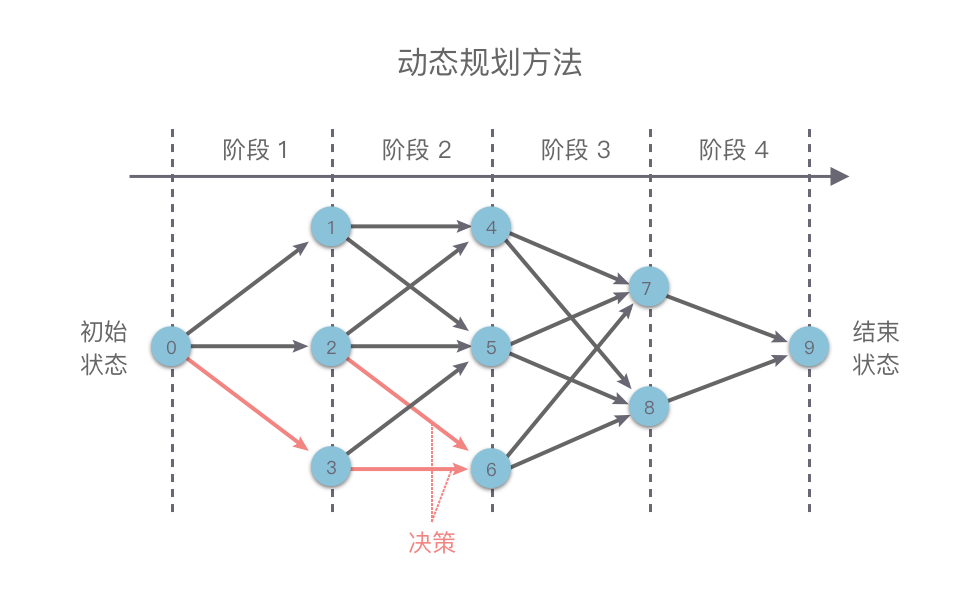
核心思想

动态规划一般用于求解具有重叠子问题和最优子结构的问题，例如最长公共子序列、背包问题、最短路径等。重叠子问题指的是在求解问题的过程中，多次用到相同的子问题，最优子结构指的是问题的最优解可以通过子问题的最优解来构造。

解题步骤

动态规划的基本步骤是：

状态定义
状态转移方程（最优子结构）
边界条件
最优解的计算

状态指的是子问题的描述信息，状态转移方程指的是子问题之间的关系，边界条件指的是最简单的子问题的解法，最优解的计算则是通过递推或者回溯等方式得到

Leetcode 真题详解

连续子数组的最大和

解题思路：

状态定义: dp[i]表示以nums[i]结尾的连续子数组和的最大值
状态转移方程:

当 dp[i-1] > 0 时，因为此时dp[i-1]对dp[i]是正增长，一定有dp[i] = nums[i] + dp[i-1]
当 dp[i-1] <= 0 时，因为此时dp[i-1]对dp[i]是负增长，一定有dp[i] = nums[i]

public int maxSubArray(int[] nums) {
	int dp = nums[0];
	int max = dp;
	for(int i = 1 ; i < nums.length ; i++){
		dp = dp > 0 ? dp + nums[i] : nums[i];
		max = Math.max(max, dp);
	}
	return max;
}

最后一块石头的重量II

解题思路：

状态定义: dp[i] 表示是否能够凑出重量为 i 的石头
状态转移方程: dp[j] |= dp[j - stone]。表示如果之前能够凑出重量为 j - stone 的石头，则现在也能够凑出重量为 j 的石头
最优解计算：找到最大的能够凑出的重量 j，则最小的可能重量为 sum - 2 * j

public int lastStoneWeightII(int[] stones) {
    int sum = Arrays.stream(stones).sum();
    int target = sum / 2;
    boolean[] dp = new boolean[target + 1];
    dp[0] = true;
    for (int stone : stones) {
        for (int j = target; j >= stone; j--) {
            dp[j] |= dp[j - stone];
        }
    }
    for (int j = target; j >= 0; j--) {
        if (dp[j]) {
            return sum - 2 * j;
        }
    }
    return sum;
}