文章目录
- 笔记
- 回归
- sklearn-LASSO
- sklearn-一元线性回归
- sklearn-多元线性回归
- sklearn-岭回归
- sklearn-弹性网ElasticNet
- sklearn-逻辑回归
- sklearn-非线性逻辑回归
- 标准方程法-岭回归
- 梯度下降法-一元线性回归
- 梯度下降法-多元线性回归
- 梯度下降法-逻辑回归
- 梯度下降法-非线性逻辑回归
- 线性回归标准方程法
- 神经网络
- 线性神经网络
- 单层感知器
- KNN
- KNN算法实现(不好)
- KNN-iris
- sklearn-KNN-iris
- 决策树
- 决策树-例子
- 集成学习
- bagging
- 随机森林
- Adaboost
- Stacking
- Voting
- 贝叶斯算法
- 贝叶斯-iris
- 聚类算法
- sklearn-K-MEANS
- DBSCAN
- 主成分分析PCA
- PCA-简单例子
- 支持向量机SVM
笔记
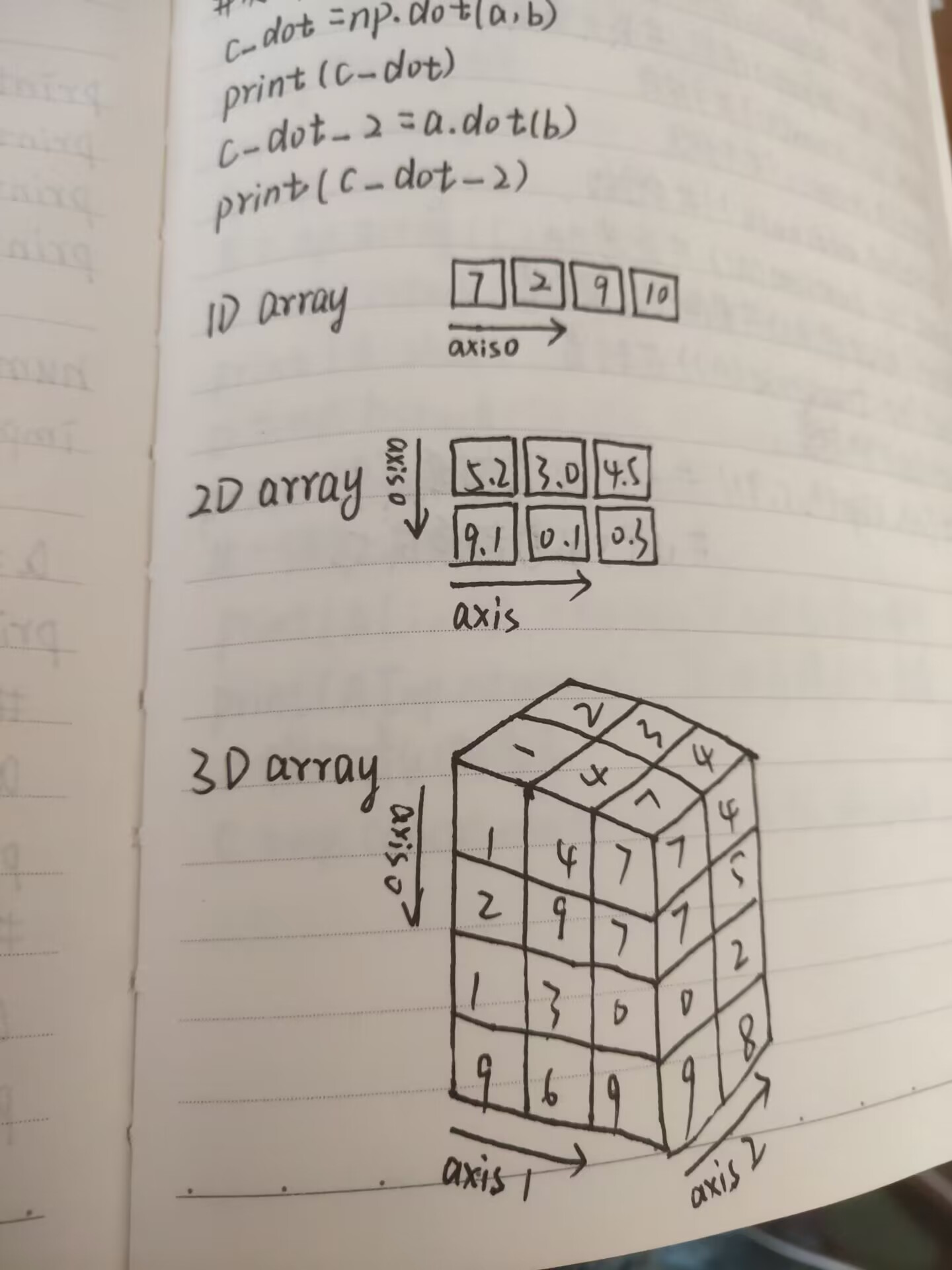
按axis=0求平均是按列求平均,最后变成一行
按axis=1求平均是按行求平均,最后变成一列
meshgrid举例
x = np.array([1, 2, 3])
y = np.array([10, 20, 30, 40])
xx, yy = np.meshgrid(x, y)
print(xx)
[[1 2 3]
[1 2 3]
[1 2 3]
[1 2 3]]
print(yy)
[[10 10 10]
[20 20 20]
[30 30 30]
[40 40 40]]
将多维数据转为一维的方法
# ravel与flatten类似,多维数据转一维。
# flatten不会改变原始数据
# ravel会改变原始数据
x.flatten()
x.ravel()
# 复制x_test
np.tile(x_test, (x_data_size, 1)) # 第一个维度复制x_data_size次,第二个维度复制1次
排序,然后留下索引值。
# 排序,然后留下索引值。
sortedDistances = distances.aragsort()
# array([1, 2, 0, 5, 3, 4]
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
"""
排序,按照关键字operator.itemgetter(1)
将classCount的键和值(items表示键和值一起)排序
"""
str() # 用于转化为字符串
np.sign()中的值如果大于0返回1,小于0返回-1
如何打乱数据:
#打乱数据
data_size = iris.data.shape[0]
index = [i for i in range(data_size)]
random.shuffle(index)
iris.data = iris.data[index]
iris.target = iris.target[index]
排序
sorted 是一个函数,适用于任何可迭代对象,返回一个新的已排序的列表。
sort 是列表对象的方法,只能用于列表,直接修改原始列表。
# 根据operator.itemgetter(1)-第1个值对classCount排序,然后再取倒序
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1), reverse=True)
使用 enumerate 函数可以方便地遍历可迭代对象并获取元素的索引和值。
for i,d in enumerate(data): # i是下标 d是数据值
回归
model.predict的时候,测试的数据是一个二维的,一维的不行。所以要通过添加一个newaxis来扩充维度
sklearn-LASSO
lasso回归使用的就是L1正则化
lasso系数 是lasso正则化里损失函数的λ,即L1正则化的系数
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)
# 切分数据
x_data = data[1:,2:] # 去掉第0行的元素,从第1行开始
y_data = data[1:,1]
print(x_data)
print(y_data)
# 创建模型
model = linear_model.LassoCV() # lasso CV是cross velidaction 交叉验证
model.fit(x_data, y_data)
# lasso系数 是lasso正则化里损失函数的λ,即L1正则化的系数
print(model.alpha_)
# 相关系数
print(model.coef_)
model.predict(x_data[-2,np.newaxis])
sklearn-一元线性回归
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()
print(x_data.shape)
x_data = data[:,0,np.newaxis]
y_data = data[:,1,np.newaxis]
# 创建并拟合模型
model = LinearRegression() # 创建线性回归模型
model.fit(x_data, y_data)
# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, model.predict(x_data), 'r')
plt.show()
sklearn-多元线性回归
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 读入数据
data = genfromtxt(r"Delivery.csv",delimiter=',')
print(data)
# 切分数据
x_data = data[:,:-1]
y_data = data[:,-1]
print(x_data)
print(y_data)
# 创建模型
model = linear_model.LinearRegression()
model.fit(x_data, y_data)
# 系数
print("coefficients:",model.coef_)
# 截距
print("intercept:",model.intercept_)
# 测试
x_test = [[102,4]]
predict = model.predict(x_test)
print("predict:",predict)
ax = plt.figure().add_subplot(111, projection = '3d')
ax.scatter(x_data[:,0], x_data[:,1], y_data, c = 'r', marker = 'o', s = 100) #点为红色三角形
x0 = x_data[:,0]
x1 = x_data[:,1]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = model.intercept_ + x0*model.coef_[0] + x1*model.coef_[1]
# 画3D图
ax.plot_surface(x0, x1, z)
#设置坐标轴
ax.set_xlabel('Miles')
ax.set_ylabel('Num of Deliveries')
ax.set_zlabel('Time')
#显示图像
plt.show()
sklearn-岭回归
岭回归就是L2正则化。L2正则化采用了岭回归
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt
# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)
# 创建模型
# 生成50个值
alphas_to_test = np.linspace(0.001, 1) # 0.001~1. 不给定则默认为50个数。为岭回归系数λ。给定了五十个,取一个最好的
# 创建模型,保存误差值
"""
RidgeCV 是岭回归(Ridge Regression)模型的交叉验证版本。
岭回归是一种线性回归的扩展,通过添加一个正则化项(L2 正则化)来控制模型的复杂度,并减小模型对输入数据的过拟合。
alpha 是用于控制正则化强度的超参数,它越大,正则化的效果越强,模型的复杂度越低。
"""
model = linear_model.RidgeCV(alphas=alphas_to_test, store_cv_values=True) # alphas表示岭回归的系数,即λ。
model.fit(x_data, y_data) # 在训练过程中,模型会进行交叉验证,并计算每个 alpha 值对应的交叉验证误差。
# 岭系数 λ
print(model.alpha_) # 该值即50个零回归系数λ中最好的一个λ
# loss值
print(model.cv_values_.shape) # (16, 50) (n_samples, n_alphas) n_samples 表示样本数量,n_alphas 表示测试的岭系数数量
"""
16 表示尝试的 n_samples 值的数量,即 给定样本中元素个数。50 表示每个 alpha 值对应的交叉验证误差的数量,即交叉验证的折数。
"""
# 画图
# 岭系数跟loss值的关系
"""
model.cv_values_.mean(axis=0) 他的shape是(16, 50) 按行取平均是所有的行加在一起,即一行。所以一共50行
"""
# print( model.cv_values_.shape, model.cv_values_.mean(axis=0).shape)
plt.plot(alphas_to_test, model.cv_values_.mean(axis=0))
# 选取的岭系数值的位置
plt.plot(model.alpha_, min(model.cv_values_.mean(axis=0)),'bo')
plt.show()
print(x_data[2])
model.predict(x_data[2,np.newaxis]) # x_data[2]是一维数据。用numpy的输入数据必须是多维的。所以加一个newaxis
sklearn-弹性网ElasticNet

import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)
# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)
# 创建模型
model = linear_model.ElasticNetCV() # 默认会选100个系数测试。最后返回1个最优的,即弹性网损失函数后面一项λ
model.fit(x_data, y_data)
# 弹性网系数 即lambda
print(model.alpha_)
# 相关系数
print(model.coef_)
model.predict(x_data[-2,np.newaxis])
sklearn-逻辑回归
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing
from sklearn import linear_model
# 数据是否需要标准化
scale = False
# 载入数据
data = np.genfromtxt("LR-testSet.csv", delimiter=",")
x_data = data[:,:-1]
y_data = data[:,-1]
def plot():
x0 = []
x1 = []
y0 = []
y1 = []
# 切分不同类别的数据
for i in range(len(x_data)):
if y_data[i]==0:
x0.append(x_data[i,0])
y0.append(x_data[i,1])
else:
x1.append(x_data[i,0])
y1.append(x_data[i,1])
# 画图
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
#画图例
plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')
plot()
plt.show()
logistic = linear_model.LogisticRegression()
logistic.fit(x_data, y_data)
"""
对于二分类模型,其决策边界通常为直线或超平面。
这里的特征是二维的,所以决策边界是一个直线。所以系数有两个,logistic.coef_是一个长度为2的列表。
"""
if scale == False:
# 画图决策边界
plot()
x_test = np.array([[-4],[3]])
y_test = (-logistic.intercept_ - x_test*logistic.coef_[0][0])/logistic.coef_[0][1] # intercept_:截距。coef是两个系数0 此为决策边界的y
plt.plot(x_test, y_test, 'k') # k是黑色的意思
plt.show()
predictions = logistic.predict(x_data)
print(classification_report(y_data, predictions))
sklearn-非线性逻辑回归
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.datasets import make_gaussian_quantiles
from sklearn.preprocessing import PolynomialFeatures
# 生成2维正态分布,生成的数据按分位数分为两类,500个样本,2个样本特征
# 可以生成两类或多类数据
x_data, y_data = make_gaussian_quantiles(n_samples=500, n_features=2,n_classes=2)
"""
生成的数据将分为两个类别,每个类别都服从高斯分布。
x_data 是生成的特征数据,是一个形状为 (500, 2) 的数组,其中每一行是一个数据点,每一列是一个特征。
y_data 是生成的目标变量,是一个长度为 500 的数组,表示每个数据点所属的类别。
"""
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
# print(np.c_[x_data[:, 0], x_data[:, 1], y_data]) # 并起来
# 建立并训练模型
logistic = linear_model.LogisticRegression()
logistic.fit(x_data, y_data)
# 画图
# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
z = logistic.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
z = z.reshape(xx.shape) # 将z的形状reshape成xx的形状
# 等高线图
cs = plt.contourf(xx, yy, z)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
print('score:',logistic.score(x_data,y_data))
# 定义多项式回归,degree的值可以调节多项式的特征
poly_reg = PolynomialFeatures(degree=5)
# 特征处理
x_poly = poly_reg.fit_transform(x_data)
print(x_data.shape, x_poly.shape)
# 定义逻辑回归模型
logistic = linear_model.LogisticRegression()
# 训练模型
logistic.fit(x_poly, y_data)
# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
z = logistic.predict(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]))# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
print('score:',logistic.score(x_poly,y_data))
逻辑回归中,画决策边界:
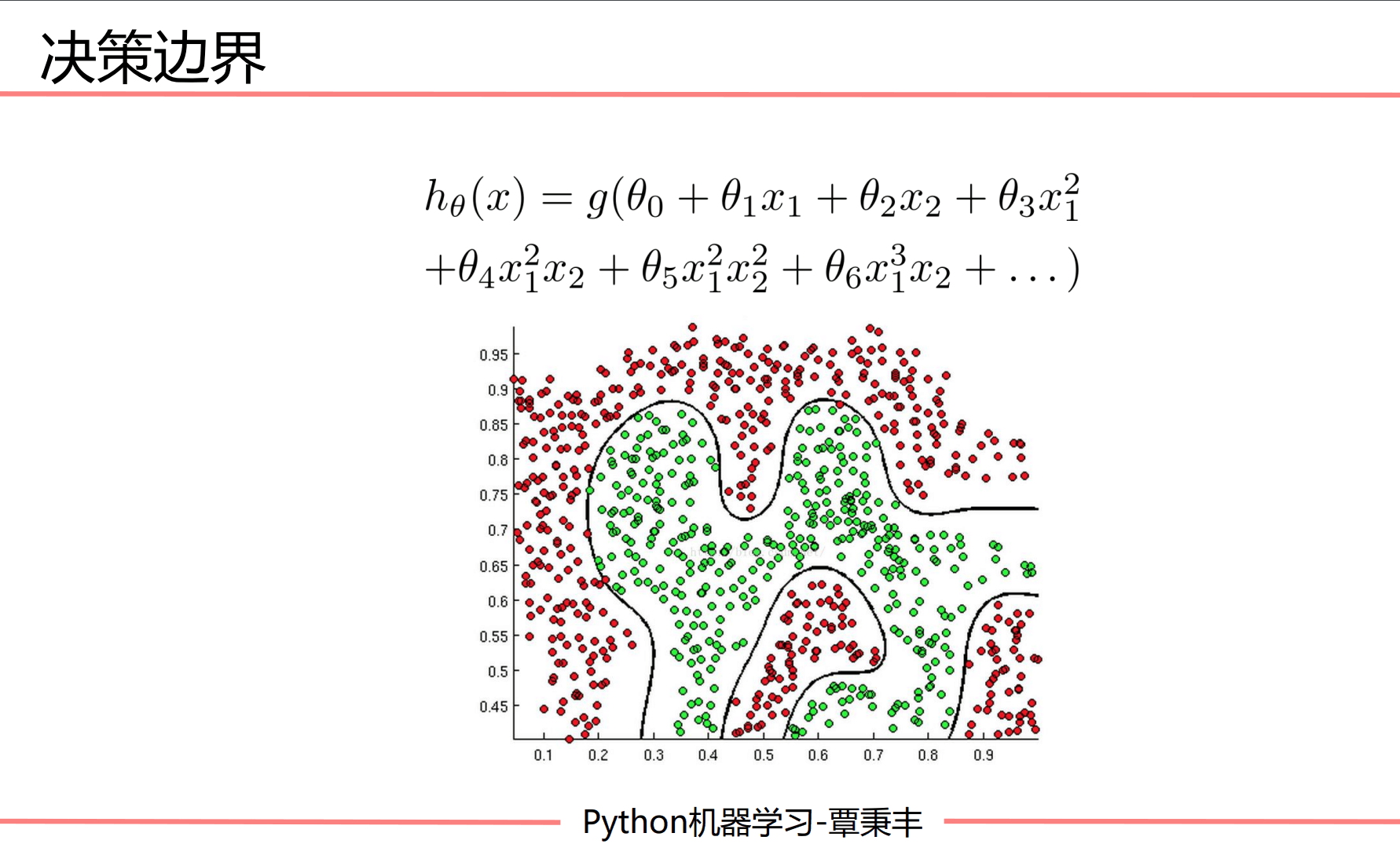
其中θi表示权重(系数),xi表示变量。如果是画一个一次的决策边界,则为:
w0 + w1x1 + w2x2 = 0
这里的w等价于θ。由于一维只有x和y,所以x1对应x, x2对应y
w0 + w1x + w2y = 0
此时y = (-w0 - w1x) / w2
标准方程法-岭回归
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)
# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1,np.newaxis]
print(x_data)
print(y_data)
print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
# 给样本添加偏置项
X_data = np.concatenate((np.ones((16,1)),x_data),axis=1)
print(X_data.shape)
# 岭回归标准方程法求解回归参数
def weights(xArr, yArr, lam=0.2):
xMat = np.mat(xArr)
yMat = np.mat(yArr)
xTx = xMat.T*xMat # 矩阵乘法
rxTx = xTx + np.eye(xMat.shape[1])*lam
# 计算矩阵的值,如果值为0,说明该矩阵没有逆矩阵
if np.linalg.det(rxTx) == 0.0:
print("This matrix cannot do inverse")
return
# xTx.I为xTx的逆矩阵
ws = rxTx.I*xMat.T*yMat
return ws
ws = weights(X_data,y_data)
print(ws)
# 计算预测值
np.mat(X_data)*np.mat(ws)
梯度下降法-一元线性回归
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()
# 学习率learning rate
lr = 0.0001
# 截距
b = 0
# 斜率
k = 0
# 最大迭代次数
epochs = 50
# 最小二乘法
def compute_error(b, k, x_data, y_data):
totalError = 0
for i in range(0, len(x_data)):
totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
return totalError / float(len(x_data)) / 2.0
def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
# 计算总数据量
m = float(len(x_data))
# 循环epochs次
for i in range(epochs):
b_grad = 0
k_grad = 0
# 计算梯度的总和再求平均
for j in range(0, len(x_data)):
b_grad += (1/m) * (((k * x_data[j]) + b) - y_data[j])
k_grad += (1/m) * x_data[j] * (((k * x_data[j]) + b) - y_data[j])
# 更新b和k
b = b - (lr * b_grad)
k = k - (lr * k_grad)
# 每迭代5次,输出一次图像
if i % 5==0:
print("epochs:",i)
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, k*x_data + b, 'r')
plt.show()
return b, k
print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
print("Running...")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))
# 画图
# plt.plot(x_data, y_data, 'b.')
# plt.plot(x_data, k*x_data + b, 'r')
# plt.show()
# meshgrid 举例
import numpy as np
x0, x1 = np.meshgrid([1,2,3], [4,5,6])
"""
x0
array([[1, 2, 3],
[1, 2, 3],
[1, 2, 3]])
x1
array([[4, 4, 4],
[5, 5, 5],
[6, 6, 6]])
"""
梯度下降法-多元线性回归
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 读入数据
data = genfromtxt(r"Delivery.csv",delimiter=',')
print(data)
# 切分数据
x_data = data[:,:-1]
y_data = data[:,-1]
print(x_data)
print(y_data)
# 学习率learning rate
lr = 0.0001
# 参数
theta0 = 0
theta1 = 0
theta2 = 0
# 最大迭代次数
epochs = 1000
# 最小二乘法
def compute_error(theta0, theta1, theta2, x_data, y_data):
totalError = 0
for i in range(0, len(x_data)):
totalError += (y_data[i] - (theta1 * x_data[i,0] + theta2*x_data[i,1] + theta0)) ** 2
return totalError / float(len(x_data))
def gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs):
# 计算总数据量
m = float(len(x_data))
# 循环epochs次
for i in range(epochs):
theta0_grad = 0
theta1_grad = 0
theta2_grad = 0
# 计算梯度的总和再求平均
for j in range(0, len(x_data)):
theta0_grad += (1/m) * ((theta1 * x_data[j,0] + theta2*x_data[j,1] + theta0) - y_data[j])
theta1_grad += (1/m) * x_data[j,0] * ((theta1 * x_data[j,0] + theta2*x_data[j,1] + theta0) - y_data[j])
theta2_grad += (1/m) * x_data[j,1] * ((theta1 * x_data[j,0] + theta2*x_data[j,1] + theta0) - y_data[j])
# 更新b和k
theta0 = theta0 - (lr*theta0_grad)
theta1 = theta1 - (lr*theta1_grad)
theta2 = theta2 - (lr*theta2_grad)
return theta0, theta1, theta2
print("Starting theta0 = {0}, theta1 = {1}, theta2 = {2}, error = {3}".
format(theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)))
print("Running...")
theta0, theta1, theta2 = gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs)
print("After {0} iterations theta0 = {1}, theta1 = {2}, theta2 = {3}, error = {4}".
format(epochs, theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)))
ax = plt.figure().add_subplot(111, projection = '3d')
ax.scatter(x_data[:,0], x_data[:,1], y_data, c = 'r', marker = 'o', s = 100) #点为红色三角形
x0 = x_data[:,0]
x1 = x_data[:,1]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = theta0 + x0*theta1 + x1*theta2
# 画3D图
ax.plot_surface(x0, x1, z)
#设置坐标轴
ax.set_xlabel('Miles')
ax.set_ylabel('Num of Deliveries')
ax.set_zlabel('Time')
#显示图像
plt.show()
梯度下降法-逻辑回归
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing
# 数据是否需要标准化
scale = True
# 载入数据
data = np.genfromtxt("LR-testSet.csv", delimiter=",")
x_data = data[:,:-1]
y_data = data[:,-1]
def plot():
x0 = []
x1 = []
y0 = []
y1 = []
# 切分不同类别的数据
for i in range(len(x_data)):
if y_data[i]==0:
x0.append(x_data[i,0])
y0.append(x_data[i,1])
else:
x1.append(x_data[i,0])
y1.append(x_data[i,1])
# 画图
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
#画图例
plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')
plot()
plt.show()
# 数据处理,添加偏置项
x_data = data[:,:-1]
y_data = data[:,-1,np.newaxis]
print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
# 给样本添加偏置项
X_data = np.concatenate((np.ones((100,1)),x_data),axis=1)
print(X_data.shape)
def sigmoid(x):
return 1.0/(1+np.exp(-x))
def cost(xMat, yMat, ws):
left = np.multiply(yMat, np.log(sigmoid(xMat*ws)))
right = np.multiply(1 - yMat, np.log(1 - sigmoid(xMat*ws)))
return np.sum(left + right) / -(len(xMat))
def gradAscent(xArr, yArr):
if scale == True:
xArr = preprocessing.scale(xArr)
xMat = np.mat(xArr)
yMat = np.mat(yArr)
lr = 0.001
epochs = 10000
costList = []
# 计算数据行列数
# 行代表数据个数,列代表权值个数
m,n = np.shape(xMat)
# 初始化权值
ws = np.mat(np.ones((n,1)))
for i in range(epochs+1):
# xMat和weights矩阵相乘
h = sigmoid(xMat*ws)
# 计算误差
ws_grad = xMat.T*(h - yMat)/m
ws = ws - lr*ws_grad
if i % 50 == 0:
costList.append(cost(xMat,yMat,ws))
return ws,costList
# 训练模型,得到权值和cost值的变化
ws,costList = gradAscent(X_data, y_data)
print(ws)
if scale == False:
# 画图决策边界
plot() # 画散点图scatter
x_test = [[-4],[3]]
y_test = (-ws[0] - x_test*ws[1])/ws[2]
plt.plot(x_test, y_test, 'k')
plt.show()
# 画图 loss值的变化
x = np.linspace(0,10000,201)
plt.plot(x, costList, c='r')
plt.title('Train')
plt.xlabel('Epochs')
plt.ylabel('Cost')
plt.show()
# 预测
def predict(x_data, ws):
if scale == True:
x_data = preprocessing.scale(x_data)
xMat = np.mat(x_data)
ws = np.mat(ws)
return [1 if x >= 0.5 else 0 for x in sigmoid(xMat*ws)]
predictions = predict(X_data, ws)
print(classification_report(y_data, predictions))
梯度下降法-非线性逻辑回归
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing
from sklearn.preprocessing import PolynomialFeatures
# 数据是否需要标准化
scale = False
# 载入数据
data = np.genfromtxt("LR-testSet2.txt", delimiter=",")
x_data = data[:,:-1]
y_data = data[:,-1,np.newaxis]
def plot():
x0 = []
x1 = []
y0 = []
y1 = []
# 切分不同类别的数据
for i in range(len(x_data)):
if y_data[i]==0:
x0.append(x_data[i,0])
y0.append(x_data[i,1])
else:
x1.append(x_data[i,0])
y1.append(x_data[i,1])
# 画图
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
#画图例
plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')
plot()
plt.show()
# 定义多项式回归,degree的值可以调节多项式的特征
poly_reg = PolynomialFeatures(degree=3)
# 特征处理
x_poly = poly_reg.fit_transform(x_data)
def sigmoid(x):
return 1.0/(1+np.exp(-x))
def cost(xMat, yMat, ws):
left = np.multiply(yMat, np.log(sigmoid(xMat*ws)))
right = np.multiply(1 - yMat, np.log(1 - sigmoid(xMat*ws)))
return np.sum(left + right) / -(len(xMat))
def gradAscent(xArr, yArr):
if scale == True:
xArr = preprocessing.scale(xArr)
xMat = np.mat(xArr)
yMat = np.mat(yArr)
lr = 0.03
epochs = 50000
costList = []
# 计算数据列数,有几列就有几个权值
m,n = np.shape(xMat)
# 初始化权值
ws = np.mat(np.ones((n,1)))
for i in range(epochs+1):
# xMat和weights矩阵相乘
h = sigmoid(xMat*ws)
# 计算误差
ws_grad = xMat.T*(h - yMat)/m
ws = ws - lr*ws_grad
if i % 50 == 0:
costList.append(cost(xMat,yMat,ws))
return ws,costList
# 训练模型,得到权值和cost值的变化
ws,costList = gradAscent(x_poly, y_data)
print(ws)
# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
# np.r_按row来组合array,
# np.c_按colunm来组合array
# >>> a = np.array([1,2,3])
# >>> b = np.array([5,2,5])
# >>> np.r_[a,b]
# array([1, 2, 3, 5, 2, 5])
# >>> np.c_[a,b]
# array([[1, 5],
# [2, 2],
# [3, 5]])
# >>> np.c_[a,[0,0,0],b]
# array([[1, 0, 5],
# [2, 0, 2],
# [3, 0, 5]])
z = sigmoid(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]).dot(np.array(ws)))# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
for i in range(len(z)):
if z[i] > 0.5:
z[i] = 1
else:
z[i] = 0
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
plot()
plt.show()
# 预测
def predict(x_data, ws):
# if scale == True:
# x_data = preprocessing.scale(x_data)
xMat = np.mat(x_data)
ws = np.mat(ws)
return [1 if x >= 0.5 else 0 for x in sigmoid(xMat*ws)]
predictions = predict(x_poly, ws)
print(classification_report(y_data, predictions))
test = [[2,3]]
# 定义多项式回归,degree的值可以调节多项式的特征
poly_reg = PolynomialFeatures(degree=3)
# 特征处理
x_poly = poly_reg.fit_transform(test)
# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
plt.scatter(xx,yy)
plt.show()
线性回归标准方程法
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0,np.newaxis]
y_data = data[:,1,np.newaxis]
plt.scatter(x_data,y_data)
plt.show()
print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
# 给样本添加偏置项
X_data = np.concatenate((np.ones((100,1)),x_data),axis=1)
print(X_data.shape)
# 标准方程法求解回归参数
def weights(xArr, yArr):
xMat = np.mat(xArr)
yMat = np.mat(yArr)
xTx = xMat.T*xMat # 矩阵乘法
# 计算矩阵的值,如果值为0,说明该矩阵没有逆矩阵
if np.linalg.det(xTx) == 0.0:
print("This matrix cannot do inverse")
return
# xTx.I为xTx的逆矩阵
ws = xTx.I*xMat.T*yMat
return ws
ws = weights(X_data,y_data)
print(ws)
# 画图
x_test = np.array([[20],[80]])
y_test = ws[0] + x_test*ws[1]
plt.plot(x_data, y_data, 'b.')
plt.plot(x_test, y_test, 'r')
plt.show()
神经网络
线性神经网络
如果是要求斜率k和偏置b:
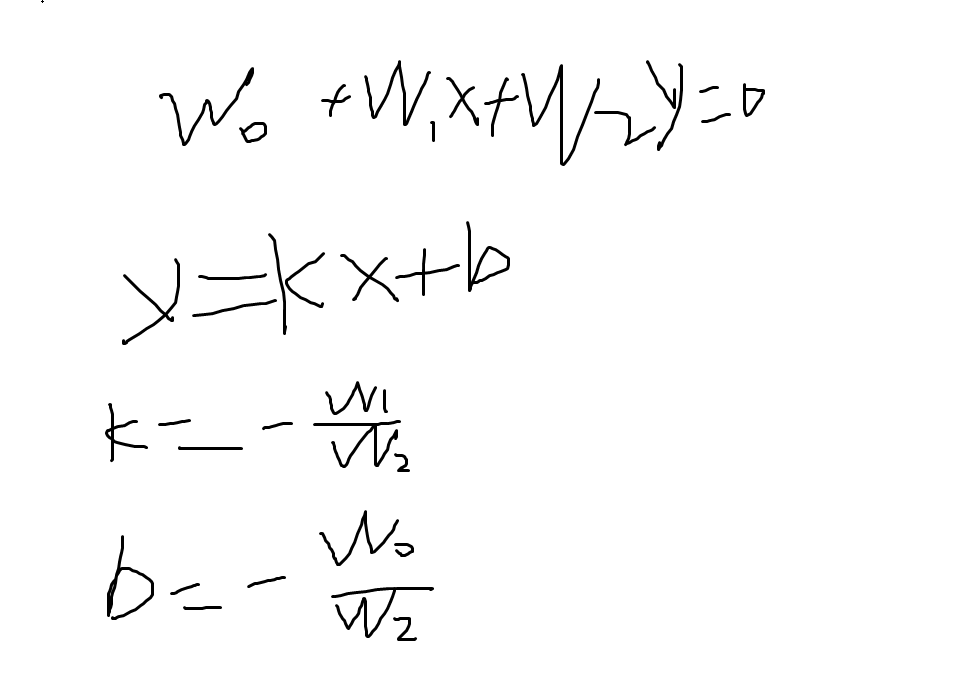
import numpy as np
import matplotlib.pyplot as plt
#输入数据
X = np.array([[1,3,3],
[1,4,3],
[1,1,1],
[1,0,2]])
#标签
Y = np.array([[1],
[1],
[-1],
[-1]])
#权值初始化,3行1列,取值范围-1到1
W = (np.random.random([3,1])-0.5)*2
print(W)
#学习率设置
lr = 0.11
#神经网络输出
O = 0
def update():
global X,Y,W,lr
O = np.dot(X,W)
W_C = lr*(X.T.dot(Y-O))/int(X.shape[0])
W = W + W_C
for _ in range(100):
update()#更新权值
#正样本
x1 = [3,4]
y1 = [3,3]
#负样本
x2 = [1,0]
y2 = [1,2]
#计算分界线的斜率以及截距
k = -W[1]/W[2]
d = -W[0]/W[2]
print('k=',k)
print('d=',d)
xdata = (0,5)
plt.figure()
plt.plot(xdata,xdata*k+d,'r')
plt.scatter(x1,y1,c='b')
plt.scatter(x2,y2,c='y')
plt.show()
单层感知器
线性神经网络是迭代100次,只看最后的结果
单层感知机是利用np.sign对分类直接变成1 -1,然后再看是否预测正确。正确则停止迭代更新权值
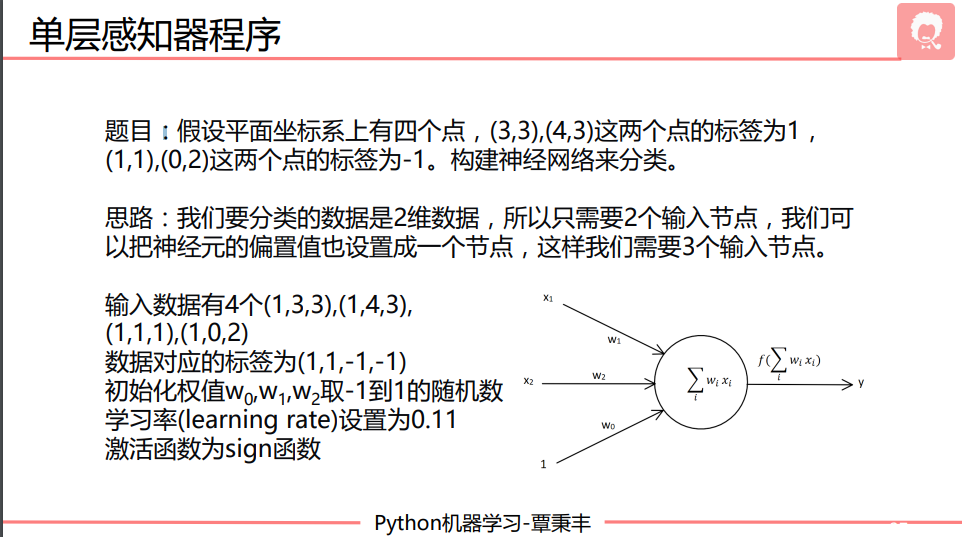
# 题目: PPT神经网络 27张
import numpy as np
import matplotlib.pyplot as plt
# 输入数据
# 四个点,每个点有3维数据,分别是点的xy坐标以及偏置值(在第0位)
X = np.array([[1,3,3],
[1,4,3],
[1,1,1],
[1,0,2]])
#标签(预测结果)
Y = np.array([[1],
[1],
[-1],
[-1]])
#权值初始化,3行1列,取值范围-1到1(本来为0-1,减0.5成-0.5~0.5,再乘2)
W = (np.random.random([3,1])-0.5)*2 # weights
print(W)
#学习率设置
lr = 0.11
#神经网络输出
O = 0
def update():
global X,Y,W,lr # 在函数内部修改全局变量的值时,global声明一下
O = np.sign(np.dot(X,W)) # O是网络输出等价于yP22 shape:(3,1) np.sign()中的值如果大于0返回1,小于0返回-1
W_C = lr*(X.T.dot(Y-O))/int(X.shape[0]) # 不希望权值每次调整都非常大,所以误差要小 要计算误差的平均值
W = W + W_C
for i in range(100):
update()#更新权值
print(W)#打印当前权值
print(i)#打印迭代次数
O = np.sign(np.dot(X,W))#输入X与权重相乘 计算当前输出
if(O == Y).all(): #.all是所有元素都相等 如果实际输出等于期望输出,模型收敛,循环结束
print('Finished')
print('epoch:',i)
break
#正样本
x1 = [3,4]
y1 = [3,3]
#负样本
x2 = [1,0]
y2 = [1,2]
#计算分界线的斜率以及截距
k = -W[1]/W[2]
d = -W[0]/W[2]
print('k=',k)
print('d=',d)
xdata = (0,5)
plt.figure()
plt.plot(xdata,xdata*k+d,'r')
plt.scatter(x1,y1,c='b')
plt.scatter(x2,y2,c='y')
plt.show()
KNN

KNN算法实现(不好)
import matplotlib.pyplot as plt
import numpy as np
import operator
# 已知分类的数据
x1 = np.array([3,2,1])
y1 = np.array([104,100,81])
x2 = np.array([101,99,98])
y2 = np.array([10,5,2])
scatter1 = plt.scatter(x1,y1,c='r')
scatter2 = plt.scatter(x2,y2,c='b')
# 未知数据
x = np.array([18])
y = np.array([90])
scatter3 = plt.scatter(x,y,c='k')
#画图例
plt.legend(handles=[scatter1,scatter2,scatter3],labels=['labelA','labelB','X'],loc='best')
plt.show()
# 已知分类的数据
x_data = np.array([[3,104],
[2,100],
[1,81],
[101,10],
[99,5],
[81,2]])
y_data = np.array(['A','A','A','B','B','B'])
x_test = np.array([18,90])
# 计算样本数量
x_data_size = x_data.shape[0]
print(x_data_size)
# 复制x_test
np.tile(x_test, (x_data_size,1)) # 将x_data按照第一个维度复制。第一个维度即列方向,增加行。复制x_data_size次
# 计算x_test与每一个样本的差值
diffMat = np.tile(x_test, (x_data_size,1)) - x_data
diffMat
# 计算差值的平方
sqDiffMat = diffMat**2
sqDiffMat
# 求和
sqDistances = sqDiffMat.sum(axis=1)
sqDistances
# print(sqDistances.shape)
# 开方
distances = sqDistances**0.5
distances
# 从小到大排序
sortedDistances = distances.argsort() # 用于返回数组排序后的索引。
sortedDistances # array([1, 2, 0, 5, 3, 4], dtype=int64)
classCount = {} # 空字典
# 设置k
k = 5
for i in range(k):
# 获取标签
votelabel = y_data[sortedDistances[i]]
# 统计标签数量
# get(key, default) default表示在字典中找不到指定键时返回的值
classCount[votelabel] = classCount.get(votelabel,0) + 1
classCount
# 根据operator.itemgetter(1)-第1个值对classCount排序,然后再取倒序
# operator.itemgetter(1) 是一个函数,用于获取字典键值对中的值。
# sortedClassCount是一个元组,从字典转变为元组
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1), reverse=True)
sortedClassCount
# 获取数量最多的标签
knnclass = sortedClassCount[0][0]
knnclass
KNN-iris
# 导入算法包以及数据集
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,confusion_matrix
import operator
import random
def knn(x_test, x_data, y_data, k):
# 计算样本数量
x_data_size = x_data.shape[0]
# 复制x_test
np.tile(x_test, (x_data_size,1))
# 计算x_test与每一个样本的差值
diffMat = np.tile(x_test, (x_data_size,1)) - x_data
# 计算差值的平方
sqDiffMat = diffMat**2
# 求和
sqDistances = sqDiffMat.sum(axis=1)
# 开方
distances = sqDistances**0.5
# 从小到大排序
sortedDistances = distances.argsort()
classCount = {}
for i in range(k):
# 获取标签
votelabel = y_data[sortedDistances[i]]
# 统计标签数量
classCount[votelabel] = classCount.get(votelabel,0) + 1
# 根据operator.itemgetter(1)-第1个值对classCount排序,然后再取倒序
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1), reverse=True)
# 获取数量最多的标签
return sortedClassCount[0][0]
# 载入数据
iris = datasets.load_iris()
# x_train,x_test,y_train,y_test = train_test_split(iris.data, iris.target, test_size=0.2) #分割数据0.2为测试数据,0.8为训练数据
#打乱数据
data_size = iris.data.shape[0]
index = [i for i in range(data_size)]
random.shuffle(index)
iris.data = iris.data[index]
iris.target = iris.target[index]
#切分数据集
test_size = 40
x_train = iris.data[test_size:]
x_test = iris.data[:test_size]
y_train = iris.target[test_size:]
y_test = iris.target[:test_size]
predictions = []
for i in range(x_test.shape[0]):
predictions.append(knn(x_test[i], x_train, y_train, 5))
print(classification_report(y_test, predictions))
print(confusion_matrix(y_test,predictions))
sklearn-KNN-iris
# 导入算法包以及数据集
from sklearn import neighbors
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import random
# 载入数据
iris = datasets.load_iris()
print(iris)
# 打乱数据切分数据集
# x_train,x_test,y_train,y_test = train_test_split(iris.data, iris.target, test_size=0.2) #分割数据0.2为测试数据,0.8为训练数据
#打乱数据
data_size = iris.data.shape[0]
index = [i for i in range(data_size)]
random.shuffle(index)
iris.data = iris.data[index]
iris.target = iris.target[index]
#切分数据集
test_size = 40
x_train = iris.data[test_size:]
x_test = iris.data[:test_size]
y_train = iris.target[test_size:]
y_test = iris.target[:test_size]
# 构建模型
model = neighbors.KNeighborsClassifier(n_neighbors=3)
model.fit(x_train, y_train)
prediction = model.predict(x_test)
print(classification_report(y_test, prediction))
决策树


取信息增益最大的来当作决策树的根节点
举例:

决策树-例子
from sklearn.feature_extraction import DictVectorizer
from sklearn import tree
from sklearn import preprocessing
import csv
# 读入数据
Dtree = open(r'AllElectronics.csv', 'r')
reader = csv.reader(Dtree)
# 获取第一行数据
headers = reader.__next__()
print(headers)
# 定义两个列表
featureList = []
labelList = []
for row in reader:
# 把label存入list
labelList.append(row[-1])
rowDict = {}
for i in range(1, len(row)-1): # [1, len(row)-1) row的下标从0开始,所以得不到1234....
# 建立一个数据字典
rowDict[headers[i]] = row[i]
# 把数据字典存入list
featureList.append(rowDict)
for feature in featureList:
print(feature)
# 把数据转换成01表示 不能分析字符串,只能分析字符。
vec = DictVectorizer()
x_data = vec.fit_transform(featureList).toarray()
print("x_data:\n " + str(x_data)) # 将所有的属性写出来,然后0 1分别代表该属性是否取到
# 打印属性名称
print(vec.get_feature_names_out())
# 打印标签
print("labelList: " + str(labelList))
# 把标签转换成01表示
lb = preprocessing.LabelBinarizer()
y_data = lb.fit_transform(labelList)
print("y_data: " + str(y_data))
# 创建决策树模型
model = tree.DecisionTreeClassifier(criterion='entropy') # entropy熵 使用c4.5 gimi是
# 输入数据建立模型
model.fit(x_data, y_data)
# 测试
x_test = x_data[0]
print("x_test: " + str(x_test))
"""
执行x_test.reshape(1, -1)将
[0. 0. 1. 0. 1. 1. 0. 0. 1. 0.]
变成
[[0. 0. 1. 0. 1. 1. 0. 0. 1. 0.]]
"""
predict = model.predict(x_test.reshape(1,-1))
print("predict: " + str(predict))
# 导出决策树
# pip install graphviz
# http://www.graphviz.org/
import graphviz
dot_data = tree.export_graphviz(model,
out_file = None,
feature_names = vec.get_feature_names_out(),
class_names = lb.classes_,
filled = True,
rounded = True,
special_characters = True)
graph = graphviz.Source(dot_data)
graph.render('computer') # render 方法通常用于生成输出文件或以图像或交互窗口的形式显示图形。
graph
集成学习

bagging

# 导入算法包以及数据集
from sklearn import neighbors
from sklearn import datasets
from sklearn.ensemble import BaggingClassifier
from sklearn import tree
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
iris = datasets.load_iris()
x_data = iris.data[:, :2] # 取0 1两列数据 因为要将数据可视化到二位平面上,所以只能取2个特征
y_data = iris.target
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data) # 默认按照3/4 1/4的比例分割
# 画图
def plot(model):
# 获取数据值所在的范围 这里的x y是坐标
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
z = model.predict(np.c_[xx.ravel(), yy.ravel()]) # np.c_ 上下堆叠数组
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 画图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data) # c表示颜色 按照颜色不同画散点图
plt.show()
# 准确率
print("当前模型", model, "的准确率:", model.score(x_test, y_test))
# 使用knn进行预测
knn = neighbors.KNeighborsClassifier()
knn.fit(x_train, y_train)
plot(knn)
# 使用决策树预测
dtree = tree.DecisionTreeClassifier()
dtree.fit(x_data, y_data)
plot(dtree)
# 使用集成学习bagging + knn
bagging_knn = BaggingClassifier(knn, n_estimators=100) # knn是传入的模型, n_estimators表示做多少次又放回的抽样
bagging_knn.fit(x_train, y_train)
plot(bagging_knn)
# 使用集成学习bagging + 决策树
bagging_tree = BaggingClassifier(dtree, n_estimators=100)
# 输入数据建立模型
bagging_tree.fit(x_train, y_train)
plot(bagging_tree)
思想:
对数据进行不同次的抽样,得到n个数据集。使用这n个数据集对模型进行训练得到n个模型。然后新数据到来时,前面的n个模型会有不同的预测结果。选取多数的预测结果为最终结果。
随机森林
from sklearn import tree
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt("LR-testSet2.txt", delimiter=",")
x_data = data[:, :-1] # 除了最后一列都不取
y_data = data[:, -1]
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
x_train,x_test,y_train,y_test = train_test_split(x_data, y_data, test_size = 0.5) # test_size用于指定测试机的大小
def plot(model):
# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
z = model.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 样本散点图
plt.scatter(x_test[:, 0], x_test[:, 1], c=y_test)
plt.show()
print("当前模型", model, "的准确率:", model.score(x_test, y_test))
# 决策树模型
dtree = tree.DecisionTreeClassifier()
dtree.fit(x_train, y_train)
plot(dtree)
# 随机森林模型
RF = RandomForestClassifier(n_estimators=300)
RF.fit(x_train, y_train)
plot(RF)
Adaboost



import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_gaussian_quantiles
from sklearn.metrics import classification_report
# 生成2维正态分布,生成的数据按分位数分为2类,500个样本 2个样本特征
x1, y1 = make_gaussian_quantiles(n_samples=500, n_features=2, n_classes=2)
# 生成2维正态分布,生成的数据按分位数分成2类,400个样本,2个样本特征值均值都为3
x2, y2 = make_gaussian_quantiles(mean=(3, 3), n_samples=500, n_features=2, n_classes=2)
# 将2组数据合成1组
x_data = np.concatenate((x1,x2))
y_data = np.concatenate((y1, -y2+1)) # -y2+1是为了让模型更加复杂
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
def plot(model):
# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
z = model.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.title("name:"+str(model))
# plt.text(x=50, y=50, s=("当前模型的准确度:"+ str(model.score(x_data, y_data))))
plt.show()
# 模型的准确度
print(model.score(x_data, y_data))
# 决策树模型
model = tree.DecisionTreeClassifier(max_depth=3)
# 训练模型
model.fit(x_data, y_data)
plot(model) # 画出决策树模型的图
# AdaBoost模型
model = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3), n_estimators=10) # n_estimators表示迭代次数
# 训练模型
model.fit(x_data, y_data)
plot(model) # 画出AdaBoost模型的图
Stacking
需要一个次级分类器
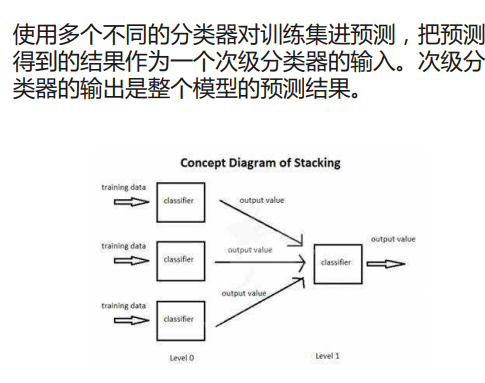

from sklearn import datasets
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from mlxtend.classifier import StackingClassifier # pip install mlxtend
import numpy as np
# 载入数据集
iris = datasets.load_iris()
# 只要1 2列
x_data, y_data = iris.data[:, 1:3], iris.target
# 定义三个不同的分类器
clf1 = KNeighborsClassifier(n_neighbors=1) # KNN 模型
clf2 = DecisionTreeClassifier() # 决策树模型
clf3 = LogisticRegression() # 逻辑回归模型
# 定义一个次级分类器
lr = LogisticRegression()
sclf = StackingClassifier(classifiers=[clf1, clf2, clf3],
meta_classifier=lr)
"""
zip函数将分类器对象(clf1、clf2、clf3、sclf)和对应的标签
('KNN'、'Decision Tree'、'LogisticRegression'、'StackingClassofier')进行了配对。
这样可以方便地同时迭代分类器和标签,并进行后续的操作。
"""
for clf, label in zip([clf1, clf2, clf3, sclf],
['KNN', 'Decision Tree', 'LogisticRegression', 'StackingClassofier']):
scores = model_selection.cross_val_score(clf, x_data, y_data, cv=3, scoring='accuracy')
print(f"Accuracy:{scores.mean()} {label}")
Voting
通过投票的方式来获得最终的预测结果。
from sklearn import datasets
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import VotingClassifier
import numpy as np
# 载入数据集
iris = datasets.load_iris()
# 只要1 2列的特征
x_data, y_data = iris.data[:, 1:3], iris.target
# 定义三个不同的分类器
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = DecisionTreeClassifier()
clf3 = LogisticRegression()
sclf = VotingClassifier([('knn', clf1), ('dtree', clf2), ('lr', clf3)])
"""
zip函数将分类器对象(clf1、clf2、clf3、sclf)和对应的标签
('KNN'、'Decision Tree'、'LogisticRegression'、'StackingClassofier')进行了配对。
这样可以方便地同时迭代分类器和标签,并进行后续的操作。
"""
for clf, label in zip([clf1, clf2, clf3, sclf],
['KNN', 'Decision Tree', 'LogisticRegression', 'StackingClassofier']):
scores = model_selection.cross_val_score(clf, x_data, y_data, cv=3, scoring='accuracy')
print(f"Accuracy:{scores.mean()} {label}")
贝叶斯算法



连续数据转为离散数据


贝叶斯-iris
# 导入算法包以及数据集
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,confusion_matrix
from sklearn.naive_bayes import MultinomialNB,BernoulliNB,GaussianNB
# 载入数据
iris = datasets.load_iris()
x_train,x_test,y_train,y_test = train_test_split(iris.data, iris.target)
# 多项式模型
mul_nb = MultinomialNB()
mul_nb.fit(x_train,y_train)
print(classification_report(mul_nb.predict(x_test),y_test))
print(confusion_matrix(mul_nb.predict(x_test),y_test))
# 贝叶斯模型
bnl_NB = BernoulliNB()
bnl_NB.fit(x_train, y_train)
print(classification_report(bnl_NB.predict(x_test),y_test))
print(confusion_matrix(bnl_NB.predict(x_test),y_test))
# 高斯模型
gs_NB = GaussianNB()
gs_NB.fit(x_train, y_train)
print(classification_report(gs_NB.predict(x_test),y_test))
print(confusion_matrix(gs_NB.predict(x_test),y_test))
聚类算法
sklearn-K-MEANS
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt("kmeans.txt", delimiter=" ")
# 设置k值
k = 4
# 训练模型
model = KMeans(n_clusters=k)
model.fit(data)
# 分类中心点坐标
centers = model.cluster_centers_
print(centers)
# 预测结果
result = model.predict(data)
print(result)
# 画出各个数据点,用不同颜色表示分类
mark = ['or', 'ob', 'og', 'oy']
for i,d in enumerate(data):
plt.plot(d[0], d[1], mark[result[i]])
# 画出各个分类的中心点
mark = ['*r', '*b', '*g', '*y']
for i,center in enumerate(centers):
plt.plot(center[0],center[1], mark[i], markersize=20)
plt.show()
# 获取数据值所在的范围
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
z = model.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 显示结果
# 画出各个数据点,用不同颜色表示分类
mark = ['or', 'ob', 'og', 'oy']
for i,d in enumerate(data):
plt.plot(d[0], d[1], mark[result[i]])
# 画出各个分类的中心点
mark = ['*r', '*b', '*g', '*y']
for i,center in enumerate(centers):
plt.plot(center[0],center[1], mark[i], markersize=20)
plt.show()
DBSCAN

sklearn-DBSCAN1
from sklearn.cluster import DBSCAN
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt("kmeans.txt", delimiter=" ")
# 训练模型
# eps距离阈值,min_samples核心对象在eps领域的样本数阈值
model = DBSCAN(eps=1.5, min_samples=4)
model.fit(data)
result = model.fit_predict(data)
# 画出各个数据点,用不同颜色表示分类
mark = ['or', 'ob', 'og', 'oy', 'ok', 'om']
for i,d in enumerate(data):
plt.plot(d[0], d[1], mark[result[i]])
plt.show()
主成分分析PCA
做的就是一个数据压缩。二维压缩成一维,三维压缩成二维,一维

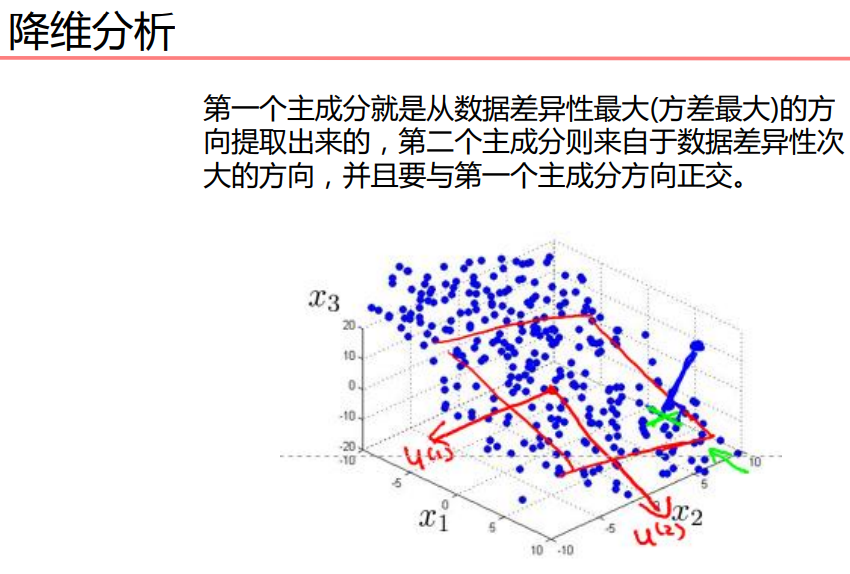
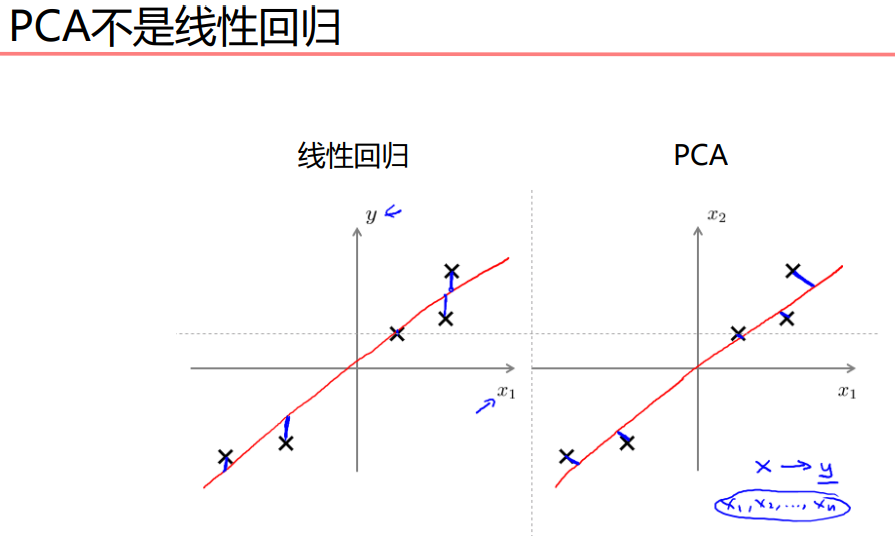
方差描述一个数据的离散程度
协方差秒数两个数据的相关性,接近1就是正相关,接近-1就是负相关。接近0就是不相关。

PCA-简单例子
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()
print(x_data.shape)
# 数据中心化
def zeroMean(dataMat):
# 按列求平均,即各个特征的平均
meanVal = np.mean(dataMat, axis=0) # (2,) dataMat:(100, 2)
print(meanVal.shape, dataMat.shape)
newData = dataMat - meanVal
# print("未数据中心化的数据为:\n", dataMat)
# print("平均值数据为:\n",meanVal)
# print("中心化数据之后的数据为\n",newData)
return newData, meanVal
newData,meanVal=zeroMean(data)
# np.cov用于求协方差矩阵,参数rowvar=0说明数据一行代表一个样本
covMat = np.cov(newData, rowvar=0) # 协方差矩阵
# np.linalg.eig求矩阵的特征值和特征向量
eigVals, eigVects = np.linalg.eig(np.mat(covMat)) # eigVals:特征值 eigVects:特征向量
# 对特征值从小到大排序
eigValIndice = np.argsort(eigVals)
eigValIndice
top = 1
# 最大的top个特征值的下标
n_eigValIndice = eigValIndice[-1:-(top+1):-1]
# 最大的n个特征值对应的特征向量
n_eigVect = eigVects[:,n_eigValIndice]
n_eigVect
# 低维特征空间的数据
lowDDataMat = newData*n_eigVect
lowDDataMat
# 利用低纬度数据来重构数据
reconMat = (lowDDataMat*n_eigVect.T) + meanVal
reconMat
# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
# 重构的数据
x_data = np.array(reconMat)[:,0]
y_data = np.array(reconMat)[:,1]
plt.scatter(x_data,y_data,c='r')
plt.show()