目录

1 目标问题：多阶2合1的合成问题

1.1 原始问题

1.2 合成问题要注意，合成的数量

1.3 合成问题不能用马尔科夫链来解决

2  方案1：用合成公式合成多次能解决吗？ --不能，解决不了递归的问题

3 方案2， 用条件期望和全期望公式计算

4 方案3，用VBA代码模拟

5 考虑合成玩法本身的难度

5.1 假设是2合1必成 100%概率

5.2 假如非100必成，那么每行的概率加权平均值对应多少代表了，期望达到的目标材料等级

5.3 错误方法

5.4 如果是3合1呢？

---

1 目标问题：多阶2合1的合成问题

1.1 原始问题

假设有如下合成问题：

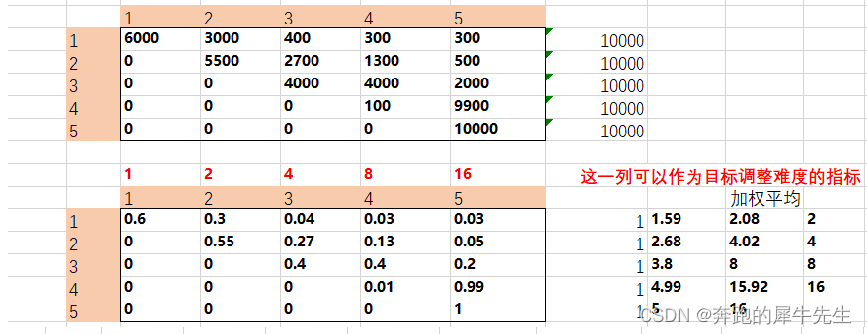
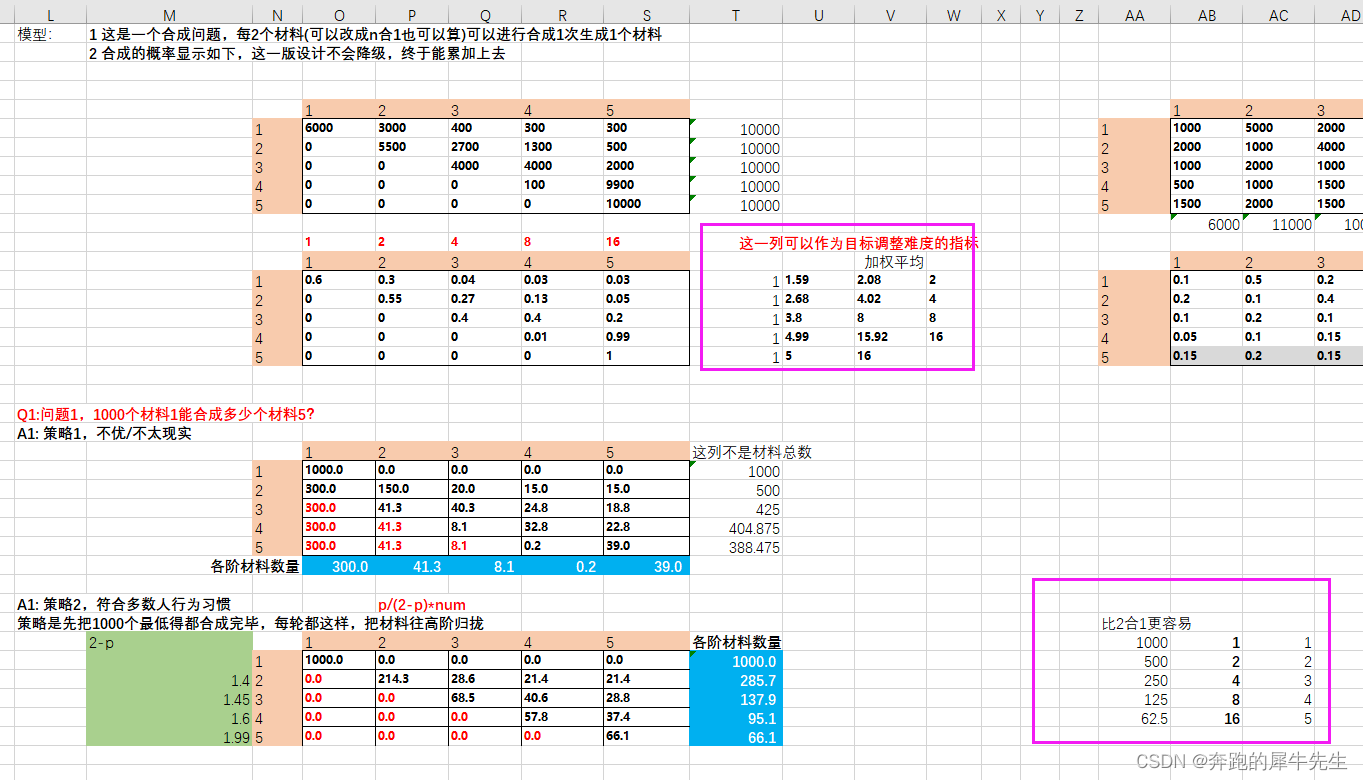
• 每次合成是2合1，随机生成一个材料，合成概率表如下
• 是个上三角矩阵，也就是说，不会往下掉级，必然都会合上去
• 假设有1000个材料1，问最后可以合成多少个材料5呢？

1.2 合成问题要注意，合成的数量

• 如假设N个材料1可以合成材料1，材料2，材料3，
• 如果是2合1，那么材料2的平均数量  2E(X)=P1*E(X)+P2*1+P3*0
• 如果是3合1，那么材料2的平均数量  3E(X)=P1*E(X)+P2*1+P3*0

1.3 合成问题不能用马尔科夫链来解决

• 合成问题不是马尔可夫那样一个状态往其他状态转移，而是多个东西变成了1个东西
• 但是可以用，条件期望的方法

2  方案1：用合成公式合成多次能解决吗？ --不能，解决不了递归的问题

• 第1次合成，把1000个材料1分别合成了材料2，材料3，材料4，材料5，也生成了1
• 第2次合成，把上一次合成的材料2合成材料3，4，5，但是材料1剩下了，也生成了2
• 第3次合成，把上一次合成的材料3合成材料4，5，但是材料1，2剩下了，也生成了3
• 第4次合成，把上一次合成的材料4合成材料5，但是材料1，2，3剩下了，也生成了4

    这样经过4次合成，从1000个材料1变成了一堆材料1，2，3，4，5，这样的结果有意义吗？没有，因为材料1剩下了很多，还可以再次进行步骤1递归。同理材料2，3，4也是这样的。

3 方案2， 用条件期望和全期望公式计算

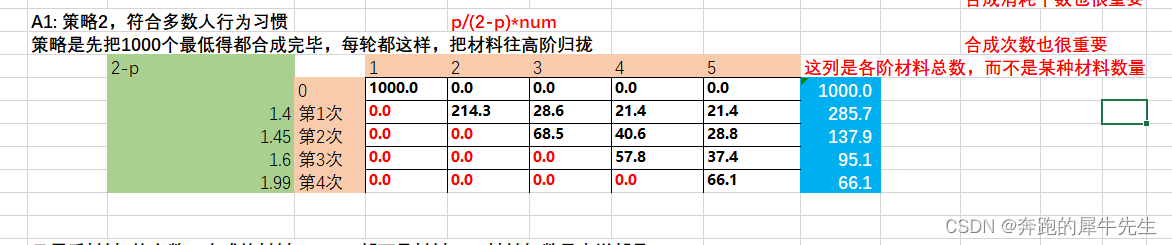
      为了避免递归问题，这次的方案策略是，每次把全部的材料1都生成为材料2，3，4，不留材料1，后面类推，这样最后剩下的就是，只剩下材料5。

     但是怎么让所有的材料1都不留下呢？ 这是个递归问题，得先用条件期望得公式列方程

• 比如先对材料1的合成列如下条件期望
• 令x= 材料1合成过程中，合成材料2得数量
• 则 2*E(X) = p1*E(X) + p2*1+ p3*0 +p4*0+p5*0
•      2*E(X) = p1*E(X) + p2*1
•         E(X) = p2/(2-p1)

    根据这个，就可以分别计算出，材料1合成过程中，材料1可以生成的材料2，3，4，5的数量，不会留下材料1。

    下面把材料2合成时，也这样计算把材料2转换为材料3，4，5，但是不留材料2本身，但是要加上第一次合成材料1时，剩下的材料3，4，5的数量。

     后面材料3合成也如此循环

     所以后最合成的处理的材料5的数量是66个。

4 方案3，用VBA代码模拟

待之后补充

5 考虑合成玩法本身的难度

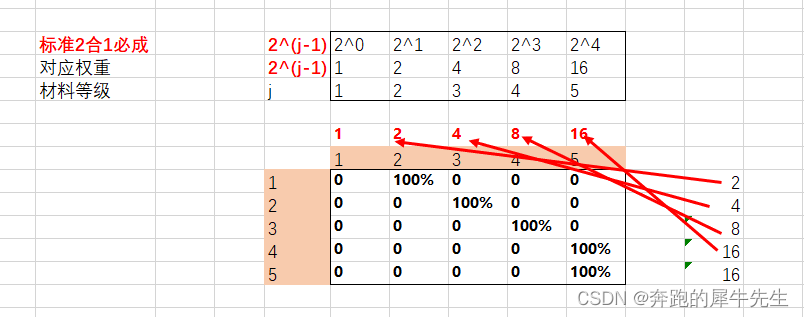
5.1 假设是2合1必成 100%概率

• 材料1，材料2，材料3，材料4，材料5，看起来材料的等级序列是1,2,3,4,5
• 但是因为合成方法是2合1，
• 比如，假设是2合1必成概率
• 1个材料2需要2各材料1，而1个材料3需要2个材料2---也就是4个材料1....
• 所以他们的权重是，1,2,4,8,16... ... 
• 可见这个加权平均值，就是这一级合成时，期望能合成的材料等级，这个可以通过调整概率来修改目标
• 因为
• 材料1--材料2，倍数是2，但是材料2与材料1相距举例是2-1（用材料1作为单位）
• 材料2--材料3，倍数是2，但是材料3与材料1相距举例是4-1（用材料1作为单位）,并不是3-1
• 材料3--材料4，倍数是2，但是材料4与材料1相距举例是8-1（用材料1作为单位）,并不是4-1
• 材料4--材料5，倍数是2，但是材料5与材料1相距举例是16-1（用材料1作为单位）,并不是5-1

• 这个2合1，看起来材料的等级1，2，3，4，5
• 实际上按权重来看，并不是这样的权重等级
• 而是2^(n-1)方,1,2,3,4,5 对应，1,2,4,8,16 这样的权重等级，这个才符合材料耗费的权重等级。
• 也就是说如果要画个纵轴，纵轴应该是权重，1,2,3,4,5 需要标记为1,2,4,8,16
• 计算出来的权重是几，也就会生成几对应的权重那一级的材料，比如第2行总权重为4，则会对应材料3！！！

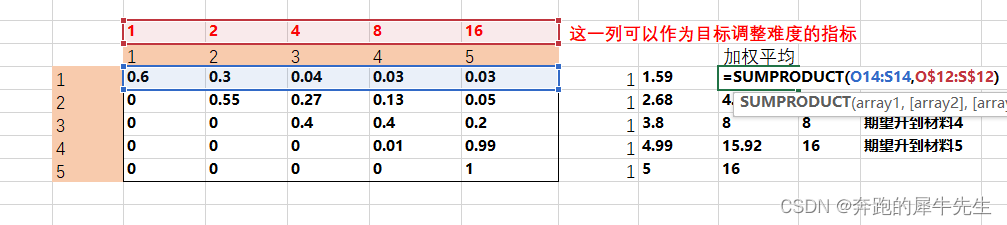
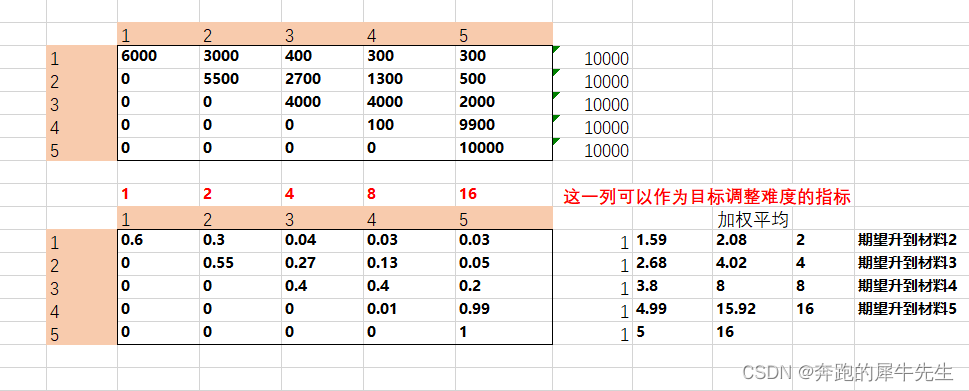
5.2 假如非100必成，那么每行的概率加权平均值对应多少代表了，期望达到的目标材料等级

• 但是，我们现在的合成概率并不是均等概率，而是如下的概率呢，那就用现在的概率当权重，计算一个 概率的加权平均值即可
• 可见这个加权平均值，就是这一级合成时，期望能合成的材料等级，这个可以通过调整概率来修改目标
• 但是要用算出来的值去匹配{1,2,4,8,16} 而不是去匹配{1,2,3,4,5}

 

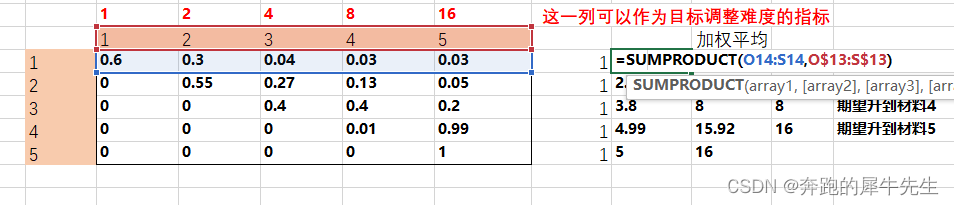
5.3 错误方法

• 如果用概率*材料等级（而不是材料的实际2合1的权重等级） 算出来的是错的，因为1,2,3,4,5 并不能代表材料1-5的难度。

5.4 如果是3合1呢？

•  如果是3合1，那就是3^n