图源:文心一言
考研对于B树的要求重点在推理手算的部分,只参考王道论坛咸鱼老师的视频就可以了;若时间非常充裕的小伙伴,也可以往下滑了解一下代码~🥝🥝
备注:
- 这次的代码是从这里复制的:B-tree (programiz.com)。因为代码比较复杂,我与AI修改的代码没有通过删除根结点的测试,因此直接借用了大佬的代码与配图。博主增加了注释,注释可能有误,小伙伴发现问题请联系博主~
- 另外,之前在博文列表中写的红黑树删除红色结点代码有问题,有需要的小伙伴也可以在这个快乐网站里查看红黑树删除代码:Deletion in a Red-Black Tree (programiz.com),有图有文,支持以下主流编程语言[python、java、c、c++]~
- 第1版:查资料、写注释~🧩🧩
参考用书:王道考研《2024年 数据结构考研复习指导》
参考用书配套视频:7.4_1_B树_哔哩哔哩_bilibili
特别感谢: Chat GPT老师、BING AI老师、文心一言老师~
📇目录
📇目录
🦮思维导图
🐳基本概念
🐋B树入门简介
🐋B树基本结构
⌨️代码实现
🧵分段代码
🔯P0:调用库文件
🔯P1:定义结点的类与树的类
🔯P2:B树结点
🔯P3:插入操作
🔯P4:删除操作
🔯P5:遍历B树
🔯P6:main函数
🧵完整代码
🔯P1:完整代码
🔯P2:执行结果
🔚结语
🦮思维导图

- 本篇仅涉及到B树:Btree的代码;
- 思维导图为整理王道教材第7章 查找的所有内容,其余学习笔记在以下博客~
- 🌸数据结构07:查找[C++][朴素二叉排序树BST]_梅头脑_的博客-CSDN博客
- 🌸数据结构07:查找[C++][平衡二叉排序树AVL]_梅头脑_的博客-CSDN博客
- 🌸数据结构07:查找[C++][红黑二叉排序树RBT]_梅头脑_的博客-CSDN博客
🐳基本概念
🐋B树入门简介
今天我们要聊聊一种特殊的树,它有着一个让人浮想联翩的名字——B树!这棵树的名字听着就像是B站“张三”一样简单、响亮而土气,但实际上是一棵不可貌相、深藏不露的树!
它的一个关键特点是每个结点可以存储多个值,而不是像普通的二叉树只能容纳一个数据。
另外,B树也像平衡二叉树、红黑二叉树一样——可以自我调节,但处理方式有有一些区别:
- 平衡树:调整相对简单一些,但是在实际插入结点过程中,由于经常触发不平衡的调整机制,导致需要频繁地调整树形,仿佛是进退两难的托孤大臣;
- 红黑树:经过优化减少了调整次数,但红黑树的成员总是难以避免看向爸爸、叔叔、爷爷甚至是儿子、侄子、孙子的脸色,仿佛是如履薄冰的中年社畜;
- B树:调整相对红黑树简单,而相对平衡树稳定。每个结点存放的数据约为自身容纳量的一半,当一个结点装满了数据,它就会找到平辈伙伴:“嘿,我装不下了,需要找个地方放这些数据!”如果兄弟也容纳不下这些数据,它们就会向父结点请求帮助,寻找一个合适的位置来存放额外的数据~
当然,B树也有一些限制。它需要严格遵守一些规则,比如结点中的值必须按照一定的顺序排列,让我们更容易找到需要的关键字。
因此,B树可以高效地处理大量的数据,它在数据库、文件系统、操作系统,甚至是人工智能的图像处理、机器学习、自然语言处理等领域也有着广泛的应用。
不过,B树本身的代码也很——毕竟普通二叉树代码100+,平衡二叉树代码150+,红黑树代码250+,B树代码300+;这点代码的增长量,虽然对于电脑来说算是蚍蜉撼树,但是对于考试来说绝对是泰山压顶,可能要把卷子写到溢出来~
🐋B树基本结构
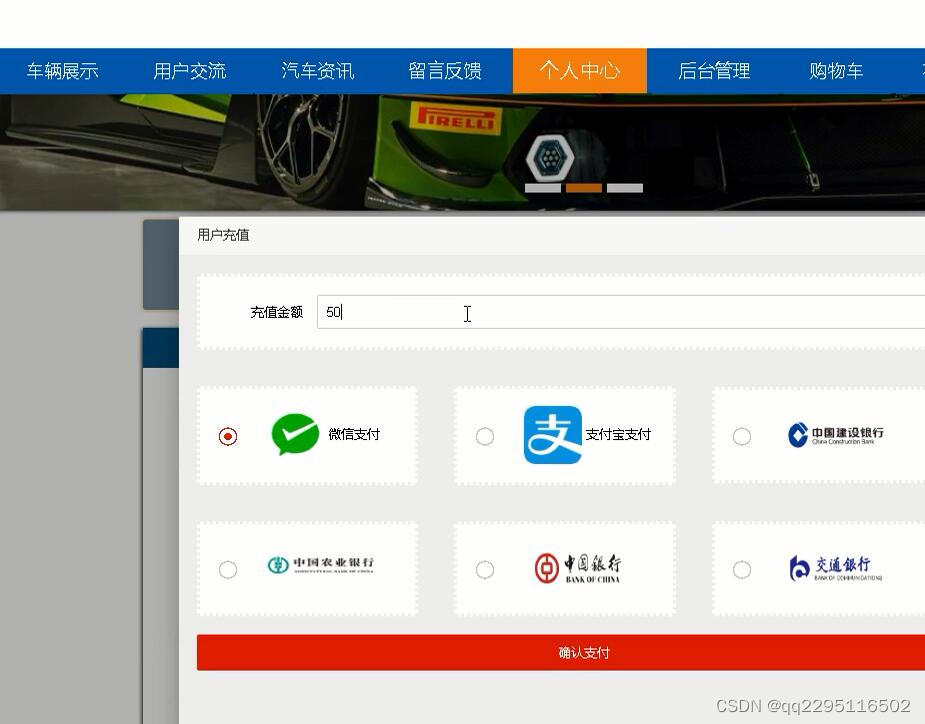
那么,B树大家族是如何处理海量数据的呢?它是以类似于小组的形式存放结点,保证结点内关键字的数量趋向于持恒或者盈满。萌新结点如果想拜入m阶B树的公会,入会须知:
| 名称 | 数量 | 子树指针 | 关键字 | 子树指针 | 关键字 | ... | 关键字 | 子树指针 |
| 符号 | n | P0 | K1 | P1 | K2 | ... | Kn | Pn |
- 每个小组的组成:
- 关键字K、指针P、数量n;
- 关键字K:结点中存储的数据,这些关键字就像是常驻本层小组的组员,按数值大小顺序排列,默认从小到大排列,即K1 < K2 < ... < Kn;
- 指针P:Ki < Pi < Ki+1,这些指针就像是传令员,如果在本层找不到对应的关键字K,但也能锁定结点的范围,对应该关键字范围的传令员就会揣着任务奔向下一层的小组员;
- 结点的关键字数量n:记录本层有多少个关键字,它是决定数据在插入、删除时是否向兄弟结点甚至是父结点借位置的关键;
- 每个小组最多容纳结点数:
- 树中的每个结点至多有m棵子树,即至多含有m-1个关键字;
- 每个小组最少容纳结点数:
- 根结点:若根结点不是叶结点,则至少有2棵子树;
- 分支结点:除根结点以外的所有非叶结点至少有⌈m/2 ⌉棵子树,即至少含有⌈m/2 ⌉-1个关键字;
- 叶子结点:没有数据的虚拟结点,所有的叶结点都出现在同一层次上,如果指针P找到了叶结点,那就说明查找失败了。
每个结点至少含有⌈m/2 ⌉-1个关键字,这样设计的好处在于,保证了B树的小组人员不会太少,若组员太少会导致在相同容量下B树很空或者深度较大,降低查找效率。
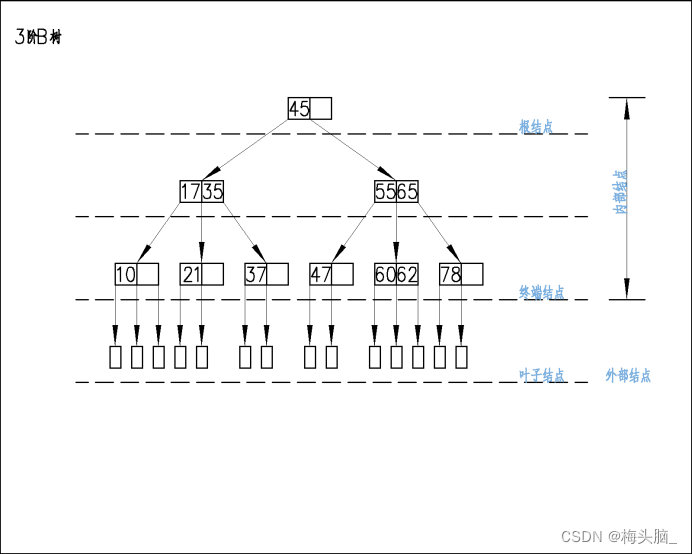
举个栗子,例如以下这棵树的阶数是m=3,则:
- 结点中最少关键字K是⌈m/2 ⌉-1 = ⌈3/2 ⌉-1=1个,此时对应的子树指针P是1+1=2个;
- 结点中最多关键字K是m-1 = 3-1 = 2个,此时对应的子树指针P是2+1=3个。
后面我们以代码+图的形式,说明如何创建一棵B树~

图源:文心一言
⌨️代码实现
🧵分段代码
🔯P0:调用库文件
- 输入输出流文件iostream:实现输出文字的效果;配合using namespace std;,可以将输出std::cout直接简写为cout,代码看着会简洁一些~
#include <iostream>
using namespace std;🔯P1:定义结点的类与树的类
- BTreeNode 类表示 B 树的结点结构。每个结点包含键值、孩子结点的指针和其他辅助信息~
// BTreeNode类:表示B树的结点结构
class BTreeNode {
int *keys; // 指针,用于存储B树结点的关键字
int t; // B树的最小度数
BTreeNode **C; // BTreeNode 类型的指针数组,用于存储B树结点的子结点,其数量为2*t
int n; // 表示当前结点包含的关键字数量
bool leaf; // 布尔类型,用于标识当前结点是否为叶子结点
public: // 公共类:相关操作
BTreeNode(int _t, bool _leaf); // BTreeNode类的构造函数声明,初始化度数t、叶子结点leaf
void traverse(); // 遍历B树中的键值
int findKey(int k); // 寻找键值
void insertNonFull(int k); // 插入未满结点
void splitChild(int i, BTreeNode *y); // 分离已满结点
void deletion(int k); // 删除键值
void removeFromLeaf(int idx); // 从叶子结点删除键值
void removeFromNonLeaf(int idx); // 从非叶子结点删除键值
int getPredecessor(int idx); // 获取前驱结点
int getSuccessor(int idx); // 获取后继结点
void fill(int idx); // 处理删除下溢:从同级结点借用键值
void borrowFromPrev(int idx); // 处理删除下溢:向前驱结点借用键值
void borrowFromNext(int idx); // 处理删除下溢:向后继结点借用键值
void merge(int idx); // 处理删除下溢:合并结点
friend class BTree; // 友元BTree:表示BTree类可以访问BTreeNode类的私有成员
};- BTree 类表示整个 B 树结构,提供 B 树的基本功能:查找、插入、删除~
// BTree类:表示整个B树结构,提供B树基本功能:查找、插入、删除
class BTree {
BTreeNode *root; // B树的根结点
int t; // B树的最小度数
public:
BTree(int _t) { // 构造函数,用于初始化B树,接受参数:最小度数_t
root = NULL; // 根结点置空
t = _t; // 接收一个整数参数_t,并将其赋值给类成员变量t,以便在后序使用
}
void traverse() { // 遍历整个B树
if (root != NULL) // 如果根结点不为空
root->traverse(); // 调用遍历traverse()函数
}
void insertion(int k); // 增加结点
void deletion(int k); // 删除结点
};以上代码需要注意的点:
- 代码中所述的叶子结点,实际上是我们之前图中的终端结点,即最底层存有数据的结点;
- “int *keys;”B树一般采用指针定义键值,使得调整操作更加灵活,且实现一种动态数组的效果,节省空间;想想如果使用int型数组定义,可能会把数组长度定义死,然后在完成结点上溢分裂操作的时候,由于不能在满数组中插入结点,因此就会多分裂1次~
🔯P2:B树结点
- 定义了结点最小度数t[此数值为用户在main函数中定义]是如何限制结点的指针数量C与键值数量keys的
- 初始化了叶子结点类型leaf与键值数量n~
// B树结点
BTreeNode::BTreeNode(int t1, bool leaf1) {
t = t1; // 接受参数t1,赋值到结点的最小度数t
leaf = leaf1; // 接受参数leaf1,赋值到叶子结点leaf,标识本结点是否为叶子结点
keys = new int[2 * t - 1]; // 分配键值,键值数量最多为2t-1个
C = new BTreeNode *[2 * t]; // 分配孩子指针,指针数量最多为2t个
n = 0; // 成员变量n初始化为0,表示结点初始的键值数量为0
}🔯P3:插入操作
当我们要向B树中插入一个新的关键字时,我们从根结点开始,根据关键字的大小,沿着指针向下搜索,直到找到一个终端结点[必须在内部结点最底层的终端结点插入,可保证失败结点在同一层]。我以为正常思路是从终端结点往上判断,like this:
- 如果终端结点还有位置,则按照排序,插入终端结点;
- 如果终端结点没有位置,则从中间分裂终端结点,并将结点中间的关键字提到父结点;
- 如果父结点满了,我们就需要继续分裂和上移,直到找到一个不满的父结点或者创建一个新的根结点。
但是代码编写的顺序正好是逆序的,就是先判断根结点,再判断终端结点。注意因为插入结点只能在终端结点进行,所以根结点为满时也就是可以插入的路径结点均为满的时候。首先,调用insert函数:
- 如果根结点为空,则创建1个新的根结点;
- 如果根结点已满,则调用splitChild函数分裂根结点;
- 如果根结点不为空且未满,则在根结点调用InsertNonFull函数将新结点插入到终端结点;
实际上的操作,(1)在插入15时终端结点为满,导致了终端结点的分裂操作;(2)在插入17时终端结点为满,调整过程中导致了终端结点与根结点的连锁分裂操作~
注意分裂的时候都是从中间开始分裂,也就是以每个结点的最小度数t为边界进行分裂,左侧为左兄弟、右侧为右兄弟,中间挂到父结点上。

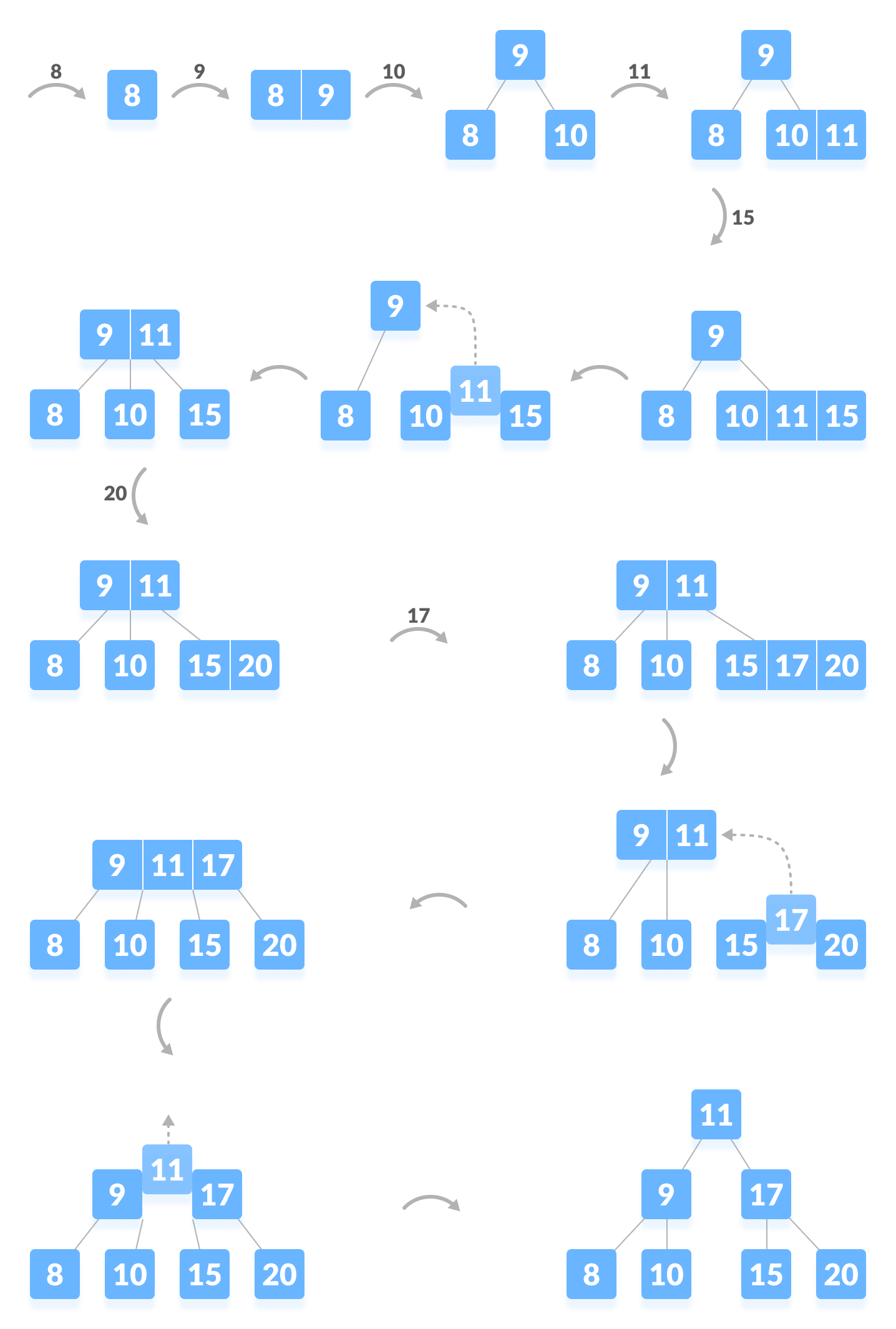
图源:Insertion into a B-tree
- 在 BTree 类中,insertion(k) 函数用于插入键值 k~
// 插入键值
void BTree::insertion(int k) {
if (root == NULL) { // 如果{根结点为空}
root = new BTreeNode(t, true); // 创建包含最小度数为t的叶子结点root
root->keys[0] = k; // 将结点的第0位设置为键值k
root->n = 1; // 将结点的键值数量n设置为1
} else { // 如果{根结点不为空}
if (root->n == 2 * t - 1) { // 如果根结点已满,即{根结点的键值数量n==2*t-1}
BTreeNode *s = new BTreeNode(t, false); // 创建包含最小度数为t的非叶子结点s
s->C[0] = root; // s结点的孩子指针C[0]指向root,即root作为s结点的第1个孩子结点
s->splitChild(0, root); // 调用splitChild,执行分裂操作
int i = 0; // 如果索引参数i=0
if (s->keys[0] < k) // 遍历结点s内的当前键值 keys是否 < k
i++;
s->C[i]->insertNonFull(k); // 在第C[i]个指针调用insertNonFull(k)
root = s; // 将s设置为根结点
} else // 如果{根结点未满}
root->insertNonFull(k); // 在根结点上调用insertNonFull(k),在叶子结点执行插入操作
}
}- 在 BTreeNode 类中,insertNonFull(k) 函数用于在非满结点中插入键值 k,splitChild(i, y) 函数用于拆分孩子结点 y~
// 插入键值:根结点未满
void BTreeNode::insertNonFull(int k) {
int i = n - 1; // 设置索引参数i = 结点键值数量n-1,即结点的末端
if (leaf == true) { // 如果{当前结点 是 叶子结点}
while (i >= 0 && keys[i] > k) { // 如果 i>=0,且结点内第i个键值 > 目标键值k
keys[i + 1] = keys[i]; // 将大于i的键值向右移动
i--; // i向左移动
}
keys[i + 1] = k; // 第i+1个键值设置为目标键值k
n = n + 1; // 结点内键值数量n+1
} else { // 如果{当前结点 不是 叶子结点}
while (i >= 0 && keys[i] > k) // 如果 i>=0,且结点内第i个键值 > 目标键值k
i--; // i向左移动
if (C[i + 1]->n == 2 * t - 1) { // 如果{叶子结点的数量 == 2*t-1},表示该指针指向的孩子结点已满
splitChild(i + 1, C[i + 1]); // 调用splitChild拆分子结点
if (keys[i + 1] < k) // 如果第i+1个键值 < 目标键值k,表示左子结点的键值均 < k
i++; // i向右移动,配合下一步操作,会将目标键值k 插入到 右子节点
}
C[i + 1]->insertNonFull(k); // 对于第i+1个孩子指针,递归调用insertNonFull(k),使其继续向下一个结点探索
}
}
// 插入键值:拆分孩子结点
void BTreeNode::splitChild(int i, BTreeNode *y) { // 将索引i、被拆分结点y作为参数传入
BTreeNode *z = new BTreeNode(y->t, y->leaf); // 创建结点z:继承了y结点的最小度数、与是否为叶子结点的特性
z->n = t - 1; // 结点z的键值数n = 最小度数t-1
for (int j = 0; j < t - 1; j++) // 结点z的右侧键值左移
z->keys[j] = y->keys[j + t];
if (y->leaf == false) { // 如果结点y不是终端结点
for (int j = 0; j < t; j++) // 结点z的孩子指针左移
z->C[j] = y->C[j + t];
}
y->n = t - 1; // 结点y的键值数n = 最小度数t-1
for (int j = n; j >= i + 1; j--) // 结点y中大于结点i的键值向右移动
C[j + 1] = C[j];
C[i + 1] = z; // 结点z挂在索引i的右侧,成为结点y的右兄弟
for (int j = n - 1; j >= i; j--) // 大于索引i的结点y的指针右移
keys[j + 1] = keys[j];
keys[i] = y->keys[t - 1]; // 将结点y的第t-1个键值提升为当前结点的第i个键值,即使中间结点上升到父结点
n = n + 1; // 结点y的键值数n = n+1
}🔯P4:删除操作
我以为删除结点的一般性思路是先查找[二分法向下遍历]、再删除、后调整,就像我在其它二叉树博文里介绍的思路,like this:
- 查询需要被删除的关键字;
- 删除关键字操作:
- 如果这个结点是终端结点,我们直接删除;
- 如果这个结点是非终端结点,我们在子树中找到可以替代的结点,转化为删除终端结点的操作;
- 检查删除后的树是否需要调整:
- 如果这个结点在删除前、后满足最小关键字数量限制,我们就直接调用删除,不需要做任何其他操作。
- 如果这个结点在删除前、后低于最小关键字数量限制,我们就需要借用或者合并相邻的兄弟结点来补充它。
- 如果借用或者合并导致结点低于最小关键字数量限制,我们就需要递归地向下借用、向上借用、或合并结点,直到找到一个不低于最小关键字数量限制的祖先结点或者减少B树的高度。
但是具体到代码,感觉它的思路就很巧妙,人家调换了顺序,根据每一轮的查询结果决定是否删除结点,再次注意此处代码中的叶子结点应该是我们所指的终端结点:
- 首先,通过调用 findKey(k) 函数,找到与目标键值 k 相等的键值在当前结点的位置索引 idx。
- 然后,根据找到的索引 idx,判断目标键值 k 是否存在于当前结点:
- 如果找到了目标键值 k(idx < n && keys[idx] == k),则根据当前结点的类型(叶子结点或非叶子结点)调用相应的删除函数:
- 如果当前结点是叶子结点,则调用 removeFromLeaf(idx) 函数来从叶子结点中删除该键值。
- 如果当前结点是非叶子结点,则调用 removeFromNonLeaf(idx) 函数来从非叶子结点中删除该键值。
- 如果在当前结点中未找到目标键值 k,则需要进一步处理:
- 首先,判断当前结点是否为叶子结点。如果是叶子结点,则输出提示信息说明目标键值 k 不在 B 树中,并结束函数调用。
- 如果当前结点不是叶子结点,说明目标键值可能存在于当前结点的子结点中。在这种情况下,需要进一步处理:
- 使用标志变量 flag 来判断计数变量 idx 是否等于结点数量 n,即是否遍历到当前结点的尾部。
- 如果当前结点的子结点(C[idx])的键值数量小于最小度数 t(C[idx]->n < t),则调用 fill(idx) 函数来填充子结点。
- 根据前面的 flag 判断,如果目标键值 k 存在于当前结点的右侧子结点中,则递归调用 C[idx - 1]->deletion(k) 来删除该键值。
- 否则,如果目标键值 k 存在于当前结点的左侧子结点中,则递归调用 C[idx]->deletion(k) 来删除该键值。
GPT老师点评:
- 第二种思想的优势在于,它将查找和删除操作结合在一起,通过在查找过程中处理删除,可以避免多次遍历相同的路径,从而提高了删除操作的效率。特别是在B树结点较大且层次较多的情况下,这种优化对性能的改进会更明显。
- 相比之下,第一种思想中,查找和删除是两个独立的步骤,可能需要多次遍历同一路径来完成删除,导致了一些额外的开销。
- 综上所述,第二种思想中的优化让删除操作更加高效。然而,两种思想在根本上并无太大差异,实现的效果是相同的,而选择哪种思想最终取决于具体实现和编程习惯。在实际编写代码时,根据自己的需求和对B树结点的组织方式选择适合的删除思想即可。
删除终端键值包含3种调节情况,另外删除非终端键值的情况都可以转化为删除终端键值:即找到终端结点数值上的前驱或后继键值,替换本键值,然后转化为删除在终端的替身键值~
图源:https://www.programiz.com/dsa/deletion-from-a-b-tree:
第一种情况:删除终端/叶子结点不会破坏最小度数的特性,直接删除~
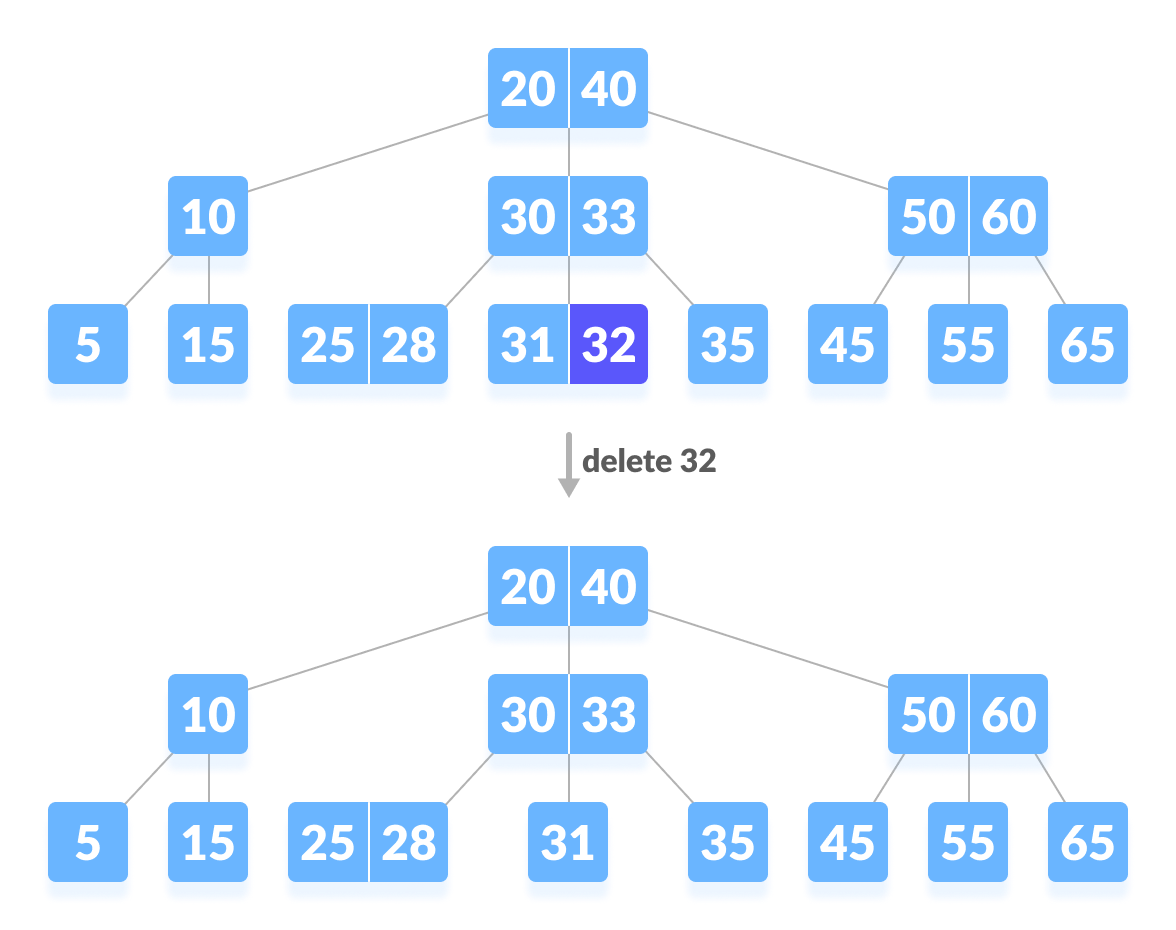
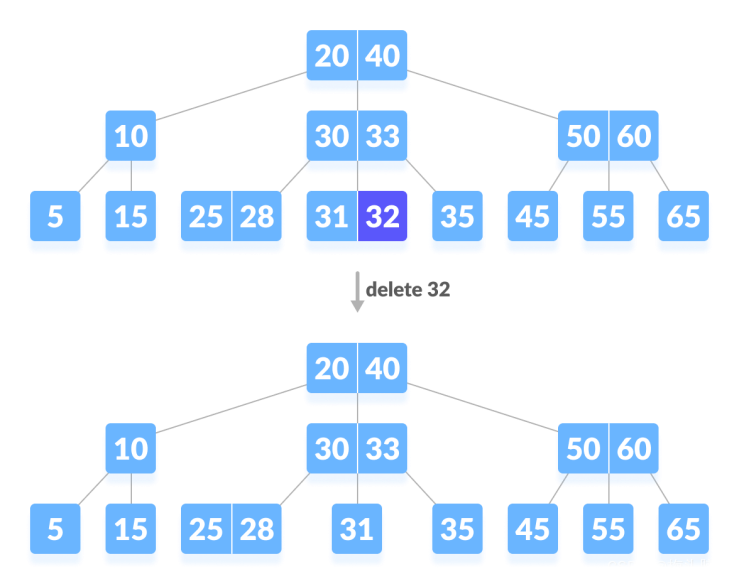
第二种情况:删除终端/叶子结点,破坏了最小度数的特性,此时看向左兄弟、右兄弟,他们够借,直接借1个数过来~
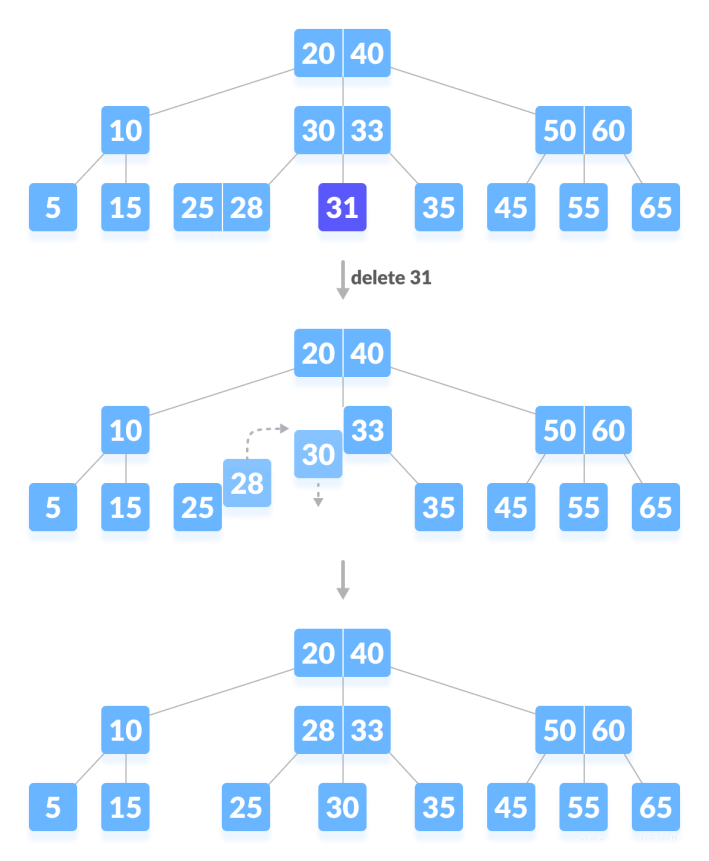
第三种情况:删除非终端/叶子结点,破坏了最小度数的特性,此时看向左兄弟、右兄弟,他们不够借,因此调用兄弟结点和父结点的数据凑到本结点,并删除兄弟结点~
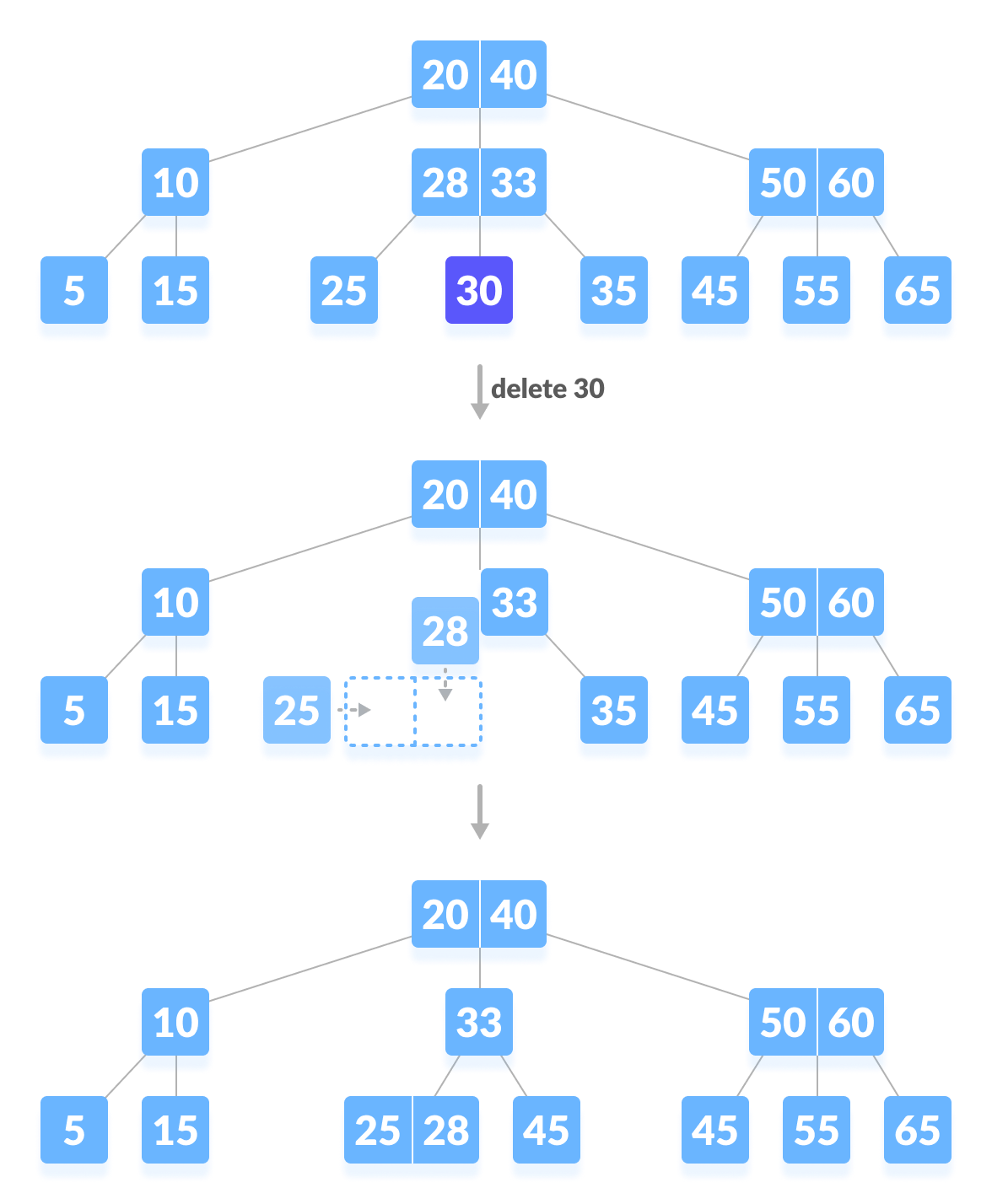
- 在 BTree 类中,deletion(k) 函数用于删除键值 k~
// 删除操作
void BTree::deletion(int k) {
if (!root) { // 如果B树为空
cout << "B树为空\n";
return;
}
root->deletion(k); // 如果B树不为空,从根结点开始调用删除函数deletion
// 以下处理特殊情况:在删除操作后根结点的键值数量为0
if (root->n == 0) { // 如果{ 根结点的键值数量n == 0 },即根结点没有键值
BTreeNode *tmp = root; // 创建tmp指针指向root,以便后续释放内存
if (root->leaf) // 如果{ 根结点root是叶子结点 }
root = NULL; // 清空root
else // 如果{ 根结点root不是叶子结点 }
root = root->C[0]; // 将root指向root的第1个孩子结点,用于替代原根结点
delete tmp; // 释放原根结点的内存空间
}
return;
}- 在 BTreeNode 类中,deletion(k) 函数用于删除键值 k,其中可能会涉及到一些下溢处理~
// 删除操作
void BTreeNode::deletion(int k) {
int idx = findKey(k); // 位置索引idx,通过调用 findkey 找到与目标键值k在当前结点中的位置索引
if (idx < n && keys[idx] == k) { // 如果表示找到了目标键值k,即{ 位置索引idx < 结点数量n } 且 { 第[idx]个键值的数值 = 需要目标数值k }
if (leaf) // 如果是叶子结点
removeFromLeaf(idx); // 调用函数 removeFromLeaf(idx);
else // 如果不是叶子结点
removeFromNonLeaf(idx); // 调用函数 removeFromNonLeaf(idx);
} else { // 如果表示未找到目标数值k,即不满足上述条件
if (leaf) { // 如果是叶子结点
cout << "键值 " << k << " 不在B树中\n"; // 输出:键值不在树中
return; // 结束函数调用
}
// 如果不是叶子结点,需要进一步处理
bool flag = ((idx == n) ? true : false); // flag:计数变量idx 是否等于 结点数量n?即判断索引idx遍历是否到结点尾部
if (C[idx]->n < t) // 处理下溢:如果当前结点的子结点(C[idx])的键值数量小于最小度数 t(C[idx]->n < t)
fill(idx); // 调用 fill(idx) 函数来填充子结点
if (flag && idx > n) // 如果目标键值 k 存在于当前结点的右侧子结点中
C[idx - 1]->deletion(k); // 递归调用 C[idx - 1]->deletion(k) 来删除该键值
else // 否则,如果目标键值 k 存在于当前结点的左侧子结点中
C[idx]->deletion(k); // 递归调用 C[idx]->deletion(k) 来删除该键值
}
return;
}
// 删除操作:寻找键值
int BTreeNode::findKey(int k) {
int idx = 0; // 位置索引idx,初始为0
while (idx < n && keys[idx] < k) // 如果 { 位置索引idx < 结点数量n } 且 { 第[idx]个键值的数值 < 需要目标数值k }
++idx; // idx+1,继续比较结点内下一个值
return idx; // 返回idx的值:如果找到了与 k 相等的键值,则返回其在结点中的索引;如果没有找到,就返回它应该插入的位置索引
}
// 删除操作:删除叶子结点关键字
void BTreeNode::removeFromLeaf(int idx) { // 将索引idx作为参数传入
for (int i = idx + 1; i < n; ++i) // 将索引移动到被删除键值之后
keys[i - 1] = keys[i]; // 将大于索引idx的键值全部向前移动一格,覆盖删除键值
n--; // 将“n”的值(结点中键的数量)减1以反映键的删除
return;
}
// 删除操作:删除非叶子结点关键字
void BTreeNode::removeFromNonLeaf(int idx) { // 将索引idx作为参数传入
int k = keys[idx]; // 创建变量k,记录被删除的键值
if (C[idx]->n >= t) { // 如果 当前结点的左子结点的有效键值数C[idx]->n ≥ 结点的最小度数t
int pred = getPredecessor(idx); // 创建变量pred,调用函数getPredecessor,记录被删除键值的前驱键值(前驱键值是左子结点的最大键值)
keys[idx] = pred; // 将前驱键值pred替换到当前结点keys[idx]
C[idx]->deletion(pred); // 删除前驱键值pred,并在左子结点递归地调用删除函数deletion
}
else if (C[idx + 1]->n >= t) { // 如果 当前结点的右子结点的有效键值数C[idx + 1] ≥ 结点的最小度数t
int succ = getSuccessor(idx); // 创建变量succ,调用函数getSuccessor,记录被删除键值的后继键值(后继键值是右子结点的最小键值)
keys[idx] = succ; // 将后继键值succ替换到当前结点keys[idx]
C[idx + 1]->deletion(succ); // 删除后继键值succ,并在右子结点递归地调用删除函数deletion
}
else { // 如果 当前结点的左、右孩子键值都不够
merge(idx); // 调用merge函数,执行结果:将右子结点的键值合并到左子节点,并删除右子结点的指针
C[idx]->deletion(k); // 删除当前键值k,并在左子结点递归地调用删除函数deletion
}
return;
}
// 删除非叶子结点关键字处理:获得前驱结点
int BTreeNode::getPredecessor(int idx) { // 将索引idx作为参数传入
BTreeNode *cur = C[idx]; // 创建指针cur,指向关键字的左孩子指针
while (!cur->leaf) // 如果当前结点不是叶子结点
cur = cur->C[cur->n]; // 指针cur指向左孩子结点的最末端结点,即结点的最大值
return cur->keys[cur->n - 1]; // 返回叶子节点的最大值,实际为将对非叶子结点的操作转化为对叶子结点的操作
}
// 删除非叶子结点关键字处理:获得后继结点
int BTreeNode::getSuccessor(int idx) { // 将索引idx作为参数传入
BTreeNode *cur = C[idx + 1]; // 创建指针cur,指向关键字的右孩子指针
while (!cur->leaf) // 如果当前结点不是叶子结点
cur = cur->C[0]; // 指针cur指向左孩子结点的最起始结点,即结点的最小值
return cur->keys[0]; // 返回叶子节点的最小值,实际为将对非叶子结点的操作转化为对叶子结点的操作
}
// 删除下溢处理:填充
void BTreeNode::fill(int idx) { // 将索引idx作为参数传入
if (idx != 0 && C[idx - 1]->n >= t) // 如果{索引idx≠0}且{当前键值的左兄弟子树 ≥ 结点最小度数t}
borrowFromPrev(idx); // 调用borrowFromPrev,向左兄弟借数据
else if (idx != n && C[idx + 1]->n >= t) // 如果{索引idx≠0}且{当前键值的右兄弟子树 ≥ 结点最小度数t}
borrowFromNext(idx); // 调用borrowFromNext,向右兄弟借数据
else { // 如果不属于以上状况,左、右兄弟都不够借
if (idx != n) // 如果{索引idx≠结点数目n},说明索引idx遍历到结点的最末端
merge(idx); // 调用merge,合并当前结点与右兄弟结点
else // 如果{索引idx=结点数目n},说明索引idx未遍历到结点的最末端
merge(idx - 1); // 调用merge,合并当前结点与左兄弟结点
}
return;
}
// 删除下溢处理:向左兄弟借数据
void BTreeNode::borrowFromPrev(int idx) { // 将索引idx作为参数传入
BTreeNode *child = C[idx]; // 创建指针child,指向当前结点的子结点C[idx]
BTreeNode *sibling = C[idx - 1]; // 创建指针sibling,指向当前结点的子结点的左兄弟结点C[idx-1]
for (int i = child->n - 1; i >= 0; --i) // 将child结点的所有键值右移1位
child->keys[i + 1] = child->keys[i];
if (!child->leaf) { // 如果child不是叶子节点
for (int i = child->n; i >= 0; --i) // 将child结点的所有指针右移1位,空出首位
child->C[i + 1] = child->C[i];
}
child->keys[0] = keys[idx - 1]; // 将当前结点的第idx - 1个键值 赋值到 child的第1个键值
if (!child->leaf) // 如果child结点不是叶子结点
child->C[0] = sibling->C[sibling->n]; // 将孩子的左兄弟结点的最后1个孩子结点指针 指向 child的第1个孩子结点指针
keys[idx - 1] = sibling->keys[sibling->n - 1]; // 将孩子的左兄弟结点的最后1个键值 赋值到 索引idx-1结点的键值
child->n += 1; // child的键值数量n+1
sibling->n -= 1; // sibling的键值数量n-1
return;
}
// 删除下溢处理:向右兄弟借数据
void BTreeNode::borrowFromNext(int idx) { // 将索引idx作为参数传入
BTreeNode *child = C[idx]; // 创建指针child,指向当前结点的子结点C[idx]
BTreeNode *sibling = C[idx + 1]; // 创建指针sibling,指向当前结点的子结点的右兄弟结点C[idx-1]
child->keys[(child->n)] = keys[idx]; // 将当前结点的索引键值 赋值到 孩子结点的最末端键值
if (!(child->leaf)) // 如果 {孩子结点 不是 叶子节点}
child->C[(child->n) + 1] = sibling->C[0]; // 右兄弟结点的首位键值指针 指向 孩子结点的末位结点的右孩子指针
keys[idx] = sibling->keys[0]; // 右兄弟结点的首位键值 赋值到 当前索引的键值
for (int i = 1; i < sibling->n; ++i) // 右兄弟结点的键值 全部左移一位,实际作用为删除右兄弟首结点的值
sibling->keys[i - 1] = sibling->keys[i];
if (!sibling->leaf) { // 如果 {右兄弟结点 不是 叶子结点}
for (int i = 1; i <= sibling->n; ++i) // 右兄弟结点的指针 全部左移一位
sibling->C[i - 1] = sibling->C[i];
}
child->n += 1; // child的键值数量n+1
sibling->n -= 1; // sibling的键值数量n-1
return;
}
// 删除下溢处理:合并当前结点与右兄弟结点
void BTreeNode::merge(int idx) { // 将索引idx作为参数传入
BTreeNode *child = C[idx]; // 创建指针child,指向当前结点的子结点C[idx]
BTreeNode *sibling = C[idx + 1]; // 创建指针sibling,指向当前结点的子结点的右兄弟结点C[idx-1]
child->keys[t - 1] = keys[idx]; // 将索引键值 赋值到 孩子结点的最小度数键值【前提:孩子结点与右兄弟结点都不满足度数】
for (int i = 0; i < sibling->n; ++i) // 将右兄弟结点的所有键值 赋值到 孩子结点的末尾
child->keys[i + t] = sibling->keys[i];
if (!child->leaf) { // 如果 {孩子结点 不是 叶子结点}
for (int i = 0; i <= sibling->n; ++i) // 将右兄弟结点的所有指针 赋值到 孩子结点的指针
child->C[i + t] = sibling->C[i];
}
for (int i = idx + 1; i < n; ++i) // 将当前结点 索引键值右侧的点全部左移,实际作用相当于删除索引值
keys[i - 1] = keys[i];
for (int i = idx + 2; i <= n; ++i) // 将当前结点 索引键值右侧的指针全部左移,除了覆盖本结点外还有最末端键值的右指针也要左移
C[i - 1] = C[i];
child->n += sibling->n + 1; // 孩子结点的数量 = 孩子结点的数量+右兄弟结点的数量+1
n--; // 当前结点的数量 - 1
delete (sibling); // 删除 兄弟结点
return;
}🔯P5:遍历B树
核心思想:先序遍历~
注意一下:如果利用索引i遍历,孩子指针会比叶子结点多1个的事情就可以了~
// 先序遍历B树
void BTreeNode::traverse() {
int i;
for (i = 0; i < n; i++) { // 当{索引i < 结点数量n}时,遍历本结点的所有键值
if (leaf == false) // 如果{当前结点 不是 叶子结点}
C[i]->traverse(); // 递归调用本函数,继续向下遍历指针
cout << " " << keys[i]; // 输出递归栈指针对应结点的值
}
if (leaf == false) // 循环结束后,如果{当前结点 不是 叶子结点}
C[i]->traverse(); // 递归调用本函数,遍历最后1个孩子指针
}🔯P6:main函数
作用就是创建了一棵小树,并且执行遍历~
int main() {
BTree t(3); // 设置B树的最小度数为3
t.insertion(8); // 插入 结点8
t.insertion(9);
t.insertion(10);
t.insertion(11);
t.insertion(15);
t.insertion(16);
t.insertion(17);
t.insertion(18);
t.insertion(20);
t.insertion(23);
cout << "B树包含的结点是: ";
t.traverse(); // 执行先序遍历
t.deletion(11); // 删除结点11
cout << "\nB树包含的结点是: ";
t.traverse(); // 执行先序遍历
}🧵完整代码
🔯P1:完整代码
写了好长好长时间的注释,删的时候发现自己都懒得删,手麻——
#include <iostream>
using namespace std;
// BTreeNode类:表示B树的结点结构
class BTreeNode {
int *keys;
int t;
BTreeNode **C;
int n;
bool leaf;
public:
BTreeNode(int _t, bool _leaf);
void traverse();
int findKey(int k);
void insertNonFull(int k);
void splitChild(int i, BTreeNode *y);
void deletion(int k);
void removeFromLeaf(int idx);
void removeFromNonLeaf(int idx);
int getPredecessor(int idx);
int getSuccessor(int idx);
void fill(int idx);
void borrowFromPrev(int idx);
void borrowFromNext(int idx);
void merge(int idx);
friend class BTree;
};
// BTree类:表示整个B树结构,提供B树基本功能:查找、插入、删除
class BTree {
BTreeNode *root;
int t;
public:
BTree(int _t) {
root = NULL;
t = _t;
}
void traverse() {
if (root != NULL)
root->traverse();
}
void insertion(int k);
void deletion(int k);
};
// B树结点
BTreeNode::BTreeNode(int t1, bool leaf1) {
t = t1;
leaf = leaf1;
keys = new int[2 * t - 1];
C = new BTreeNode *[2 * t];
n = 0;
}
// 删除操作
void BTreeNode::deletion(int k) {
int idx = findKey(k);
if (idx < n && keys[idx] == k) {
if (leaf)
removeFromLeaf(idx);
else
removeFromNonLeaf(idx);
} else {
if (leaf) {
cout << "键值" << k << "不在B树中\n";
return;
}
bool flag = ((idx == n) ? true : false);
if (C[idx]->n < t)
fill(idx);
if (flag && idx > n)
C[idx - 1]->deletion(k);
else
C[idx]->deletion(k);
}
return;
}
// 删除操作:寻找键值
int BTreeNode::findKey(int k) {
int idx = 0;
while (idx < n && keys[idx] < k)
++idx;
return idx;
}
// 删除操作:删除叶子结点关键字
void BTreeNode::removeFromLeaf(int idx) {
for (int i = idx + 1; i < n; ++i)
keys[i - 1] = keys[i];
n--;
return;
}
// 删除操作:删除非叶子结点关键字
void BTreeNode::removeFromNonLeaf(int idx) {
int k = keys[idx];
if (C[idx]->n >= t) {
int pred = getPredecessor(idx);
keys[idx] = pred;
C[idx]->deletion(pred);
}
else if (C[idx + 1]->n >= t) {
int succ = getSuccessor(idx);
keys[idx] = succ;
C[idx + 1]->deletion(succ);
}
else {
merge(idx);
C[idx]->deletion(k);
}
return;
}
// 删除非叶子结点关键字处理:获得前驱结点
int BTreeNode::getPredecessor(int idx) {
BTreeNode *cur = C[idx];
while (!cur->leaf)
cur = cur->C[cur->n];
return cur->keys[cur->n - 1];
}
// 删除非叶子结点关键字处理:获得后继结点
int BTreeNode::getSuccessor(int idx) {
BTreeNode *cur = C[idx + 1];
while (!cur->leaf)
cur = cur->C[0];
return cur->keys[0];
}
// 删除下溢处理:填充
void BTreeNode::fill(int idx) {
if (idx != 0 && C[idx - 1]->n >= t)
borrowFromPrev(idx);
else if (idx != n && C[idx + 1]->n >= t)
borrowFromNext(idx);
else {
if (idx != n)
merge(idx);
else
merge(idx - 1);
}
return;
}
// 删除下溢处理:向左兄弟借数据
void BTreeNode::borrowFromPrev(int idx) {
BTreeNode *child = C[idx];
BTreeNode *sibling = C[idx - 1];
for (int i = child->n - 1; i >= 0; --i)
child->keys[i + 1] = child->keys[i];
if (!child->leaf) {
for (int i = child->n; i >= 0; --i)
child->C[i + 1] = child->C[i];
}
child->keys[0] = keys[idx - 1];
if (!child->leaf)
child->C[0] = sibling->C[sibling->n];
keys[idx - 1] = sibling->keys[sibling->n - 1];
child->n += 1;
sibling->n -= 1;
return;
}
// 删除下溢处理:向右兄弟借数据
void BTreeNode::borrowFromNext(int idx) {
BTreeNode *child = C[idx];
BTreeNode *sibling = C[idx + 1];
child->keys[(child->n)] = keys[idx];
if (!(child->leaf))
child->C[(child->n) + 1] = sibling->C[0];
keys[idx] = sibling->keys[0];
for (int i = 1; i < sibling->n; ++i)
sibling->keys[i - 1] = sibling->keys[i];
if (!sibling->leaf) {
for (int i = 1; i <= sibling->n; ++i)
sibling->C[i - 1] = sibling->C[i];
}
child->n += 1;
sibling->n -= 1;
return;
}
// 删除下溢处理:合并当前结点与右兄弟结点
BTreeNode *child = C[idx];
BTreeNode *sibling = C[idx + 1];
child->keys[t - 1] = keys[idx];
for (int i = 0; i < sibling->n; ++i)
child->keys[i + t] = sibling->keys[i];
if (!child->leaf) {
for (int i = 0; i <= sibling->n; ++i)
child->C[i + t] = sibling->C[i];
}
for (int i = idx + 1; i < n; ++i)
keys[i - 1] = keys[i];
for (int i = idx + 2; i <= n; ++i)
C[i - 1] = C[i];
child->n += sibling->n + 1;
n--;
delete (sibling);
return;
}
// 插入键值
void BTree::insertion(int k) {
if (root == NULL) {
root = new BTreeNode(t, true);
root->keys[0] = k;
root->n = 1;
} else {
if (root->n == 2 * t - 1) {
BTreeNode *s = new BTreeNode(t, false);
s->C[0] = root;
s->splitChild(0, root);
int i = 0;
if (s->keys[0] < k)
i++;
s->C[i]->insertNonFull(k);
root = s;
} else
root->insertNonFull(k);
}
}
// 插入键值:根结点未满
void BTreeNode::insertNonFull(int k) {
int i = n - 1;
if (leaf == true) {
while (i >= 0 && keys[i] > k) {
keys[i + 1] = keys[i];
i--;
}
keys[i + 1] = k;
n = n + 1;
} else {
while (i >= 0 && keys[i] > k)
i--;
if (C[i + 1]->n == 2 * t - 1) {
splitChild(i + 1, C[i + 1]);
if (keys[i + 1] < k)
i++;
}
C[i + 1]->insertNonFull(k);
}
}
// 插入键值:拆分孩子结点
void BTreeNode::splitChild(int i, BTreeNode *y) {
BTreeNode *z = new BTreeNode(y->t, y->leaf);
z->n = t - 1;
for (int j = 0; j < t - 1; j++)
z->keys[j] = y->keys[j + t];
if (y->leaf == false) {
for (int j = 0; j < t; j++)
z->C[j] = y->C[j + t];
}
y->n = t - 1;
for (int j = n; j >= i + 1; j--)
C[j + 1] = C[j];
C[i + 1] = z;
for (int j = n - 1; j >= i; j--)
keys[j + 1] = keys[j];
keys[i] = y->keys[t - 1];
n = n + 1;
}
// 先序遍历B树
void BTreeNode::traverse() {
int i;
for (i = 0; i < n; i++) {
if (leaf == false)
C[i]->traverse();
cout << " " << keys[i];
}
if (leaf == false)
C[i]->traverse();
}
// 删除操作
void BTree::deletion(int k) {
if (!root) {
cout << "B树为空\n";
return;
}
root->deletion(k);
// 以下处理特殊情况:在删除操作后根结点的键值数量为0
if (root->n == 0) {
BTreeNode *tmp = root;
if (root->leaf)
root = NULL;
else
root = root->C[0];
delete tmp;
}
return;
}
int main() {
BTree t(3);
t.insertion(8);
t.insertion(9);
t.insertion(10);
t.insertion(11);
t.insertion(15);
t.insertion(16);
t.insertion(17);
t.insertion(18);
t.insertion(20);
t.insertion(23);
cout << "B树包含的结点是: ";
t.traverse();
t.deletion(11);
cout << "\nB树包含的结点是: ";
t.traverse();
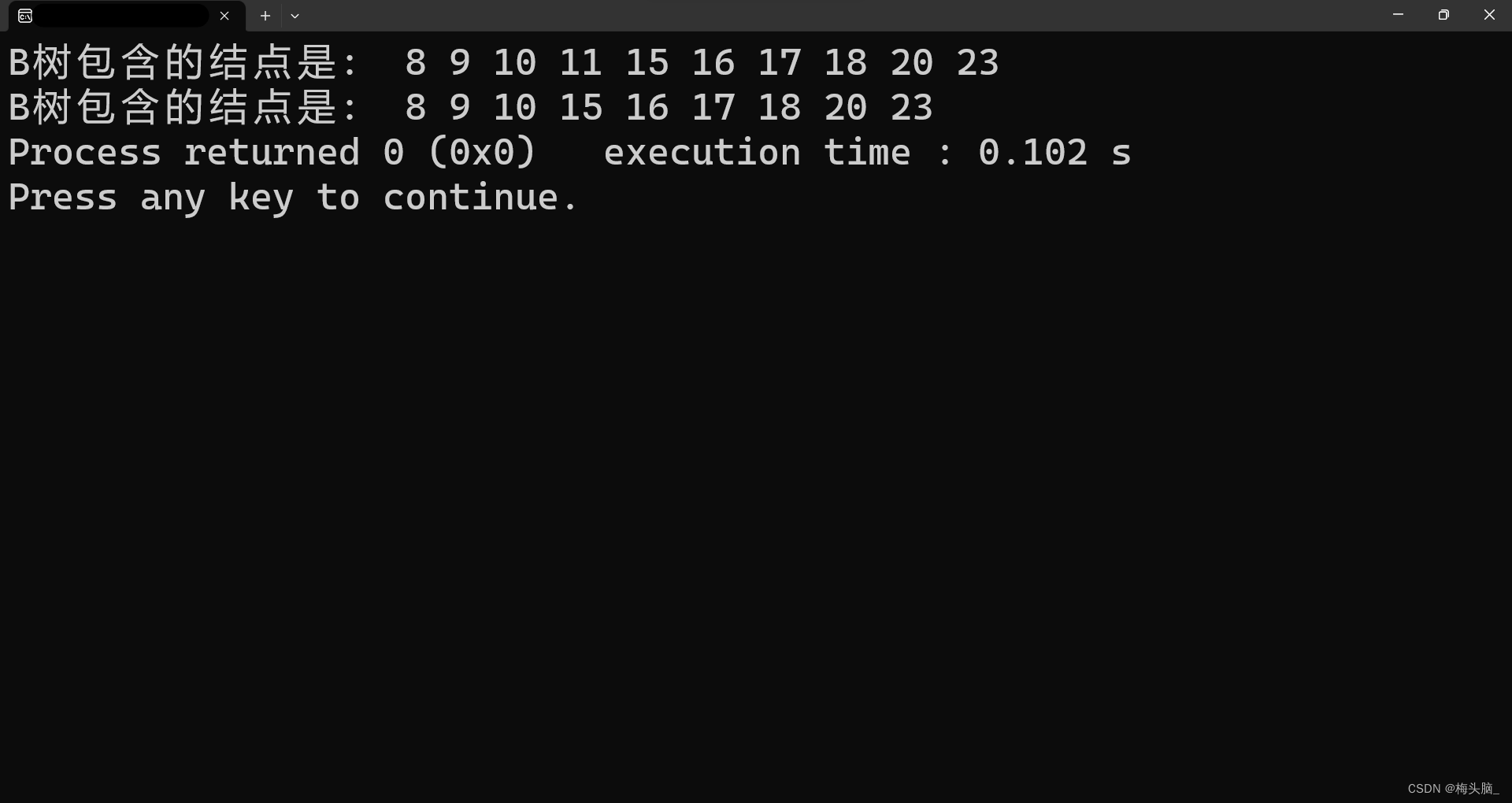
}🔯P2:执行结果
运行结果如下图所示~
🔚结语
BING AI在提示词中总是提示创作B树的诗歌,内容大概如下,我觉得还挺优美的,顺便可以用来复习本节的内容~😶🌫️
博文到此结束,写得模糊或者有误之处,欢迎小伙伴留言讨论与批评,督促博主优化内容{例如有错误、难理解、不简洁、缺功能}等~😶🌫️😶🌫️
博文若有帮助,欢迎小伙伴动动可爱的小手默默给个赞支持一下,收到点赞的话,博主肝文的动力++~🌟🌟




![[数据结构]顺序表和ArrayList](https://img-blog.csdnimg.cn/img_convert/da77b64f02e8f83a800f70616299209f.png)
![[JAVAee]线程安全](https://img-blog.csdnimg.cn/2da5976595ce40369223c4e670097fc4.png)