排序：插入、选择、交换、归并排序

news2025/1/11 20:45:42
排序 ：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
稳定性 ：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次 序保持不变，即在原序列中，r[i]=r[j] ，且 r[i] 在 r[j] 之前，而在排序后的序列中， r[i] 仍在 r[j] 之前，则称这种排 序算法是稳定的；否则称为不稳定的。
内部排序 ：数据元素全部放在内存中的排序。

外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#include <memory.h>

//打印
void PrintArray(int* a, int n);

// 排序实现的接口
// 插入排序
void InsertSort(int* a, int n);

// 希尔排序
void ShellSort(int* a, int n);

// 选择排序
void SelectSort(int* a, int n);

// 堆排序
void AdjustDwon(int* a, int n, int root);
void HeapSort(int* a, int n);

// 冒泡排序
void BubbleSort(int* a, int n);

// 快速排序递归实现
// 快速排序hoare版本
int PartSort1(int* a, int begin, int end);

//三数取中
int GetMidindex(int* a, int begin, int end);

// 快速排序挖坑法
int PartSort2(int* a, int begin, int end);

// 快速排序前后指针法
int PartSort3(int* a, int begin, int end);
void QuickSort(int* a, int left, int right);

// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right);

// 归并排序递归实现
void MergeSort(int* a, int n);

// 归并排序非递归实现
void MergeSortNonR(int* a, int n);

// 计数排序
void CountSort(int* a, int n);

#define _CRT_SECURE_NO_WARNINGS 1
#include "Sort.h"
#include "Stack.h"
//打印
void PrintArray(int* a, int n)
{
    int i = 0;
    for (i = 0; i < n; i++)
    {
        printf("%d ", a[i]);
    }
    printf("\n");
}

//插入排序  O(N^2)
void InsertSort(int* a, int n)
{
    assert(a);
    int i = 0;
    for (i = 0; i < n - 1; i++)
    {
        int end = i;
        int tmp = a[end + 1];
        //将end+1的数据插入到[0,end]有序数组中
        while (end >= 0)
        {
            if (tmp < a[end])
            {
                a[end + 1] = a[end];
                end--;
            }
            else
            {
                break;
            }
        }
        a[end + 1] = tmp;
    }
}


// 希尔排序  O(N^1.3  N^2)
void ShellSort(int* a, int n)
{
    assert(a);
    //1. gap > 1 相当于预排序，让数组接近有序
    //2. gap==1就相当于直接插入排序，保证有序
    int gap = n;
    while (gap > 1)
    {
        gap = gap / 3 + 1;//+1是保证最后一次排序gap等于1
        //gap==1，最后一次就相当于直接插入排序
        int i = 0;
        for (i = 0; i < n - gap; i++)
        {
            int end = i;
            int tmp = a[end + gap];
            while (end >= 0)
            {
                if (tmp < a[end])
                {
                    a[end + gap] = a[end];
                    end = end - gap;
                }
                else
                {
                    break;
                }
            }
            a[end + gap] = tmp;
        }
        //PrintArray(a, n);
    }
}

void Swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}

// 选择排序
// O(N^2)
void SelectSort(int* a, int n)
{
    assert(a);
    int begin = 0;
    int end = n - 1;
    while (begin < end)
    {
        int maxi = begin;
        int mini = begin;
        int i = 0;
        for (i = begin + 1; i <= end; i++)
        {
            if (a[i] > a[maxi])
            {
                maxi = i;
            }

            if (a[i] < a[mini])
            {
                mini = i;
            }
        }
        Swap(&a[mini], &a[begin]);
        //maxi和begin的位置重叠,maxi的位置需要修正
        if (maxi == begin)//max被换走了
        {
            maxi = mini;//找到max
        }
        Swap(&a[maxi], &a[end]);
        begin++;
        end--;
    }
}

// 堆排序
void AdjustDwon(int* a, int n, int root)
{
    int parent = root;
    int child = parent * 2 + 1;
    while (child < n)
    {
        //选出较大的孩子
        if (a[child + 1] > a[child] && child + 1 < n)
        {
            child++;
        }
        if (a[child] > a[parent])
        {
            Swap(&a[parent], &a[child]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}

void HeapSort(int* a, int n)
{
    //排升序，建大堆还是小堆？
    int i = 0;
    for (i = (n - 1 - 1) / 2; i >= 0 ; i--)
    {
        AdjustDwon(a, n, i);
    }
    int end = n - 1;
    while (end > 0)
    {
        Swap(&a[0], &a[end]);
        AdjustDwon(a, end, 0);
        --end;
    }
}


// 冒泡排序 O(N^2)
void BubbleSort(int* a, int n)
{
    int flag = 1;
    int i = 0;
    for (i = 0; i < n; i++)
    {
        int j = 0;
        for (j = 0; j < n - 1 - i; j++)
        {
            if (a[j] > a[j + 1])
            {
                Swap(&a[j], &a[j + 1]);
                flag = 0;
            }
        }
        //如果一趟冒泡排序过程中没有发生交换，则已经有序，不需要再进行冒泡排序
        if (flag == 1)
        {
            break;
        }
    }
}

//三数取中
int GetMidindex(int* a, int begin, int end)
{
    int mid = (begin + end) / 2 ;
    if (a[begin] < a[mid])
    {
        if (a[mid] < a[end])
        {
            return mid;
        }
        else if (a[begin] > a[end])
        {
            return begin;
        }
        else
        {
            return end;
        }
    }
    else//a[begin] > a[mid]
    {
        if (a[mid] > a[end])
        {
            return mid;
        }
        else if (a[begin] < a[end])
        {
            return begin;
        }
        else
        {
            return end;
        }
    }
}

//左右指针法
int PartSort1(int* a, int begin, int end)
{
    int mid = GetMidindex(a, begin, end);
    Swap(&a[mid], &a[end]);
    int keyindex = end;//右边做key
    while (begin < end)
    {
        //左边先走,//left < right防止在++的时候超出，而错过相遇
        while (begin < end && a[begin] <= a[keyindex])//左边找比key大,
        {
            begin++;
        }

        //右边找比key小
        while (begin < end && a[end] >= a[keyindex])
        {
            end--;
        }

        //交换left和right位置的值
        Swap(&a[begin], &a[end]);
    }
    //交换key和相遇位置的值
    Swap(&a[begin], &a[keyindex]);
    return begin;
}

// 快速排序挖坑法
int PartSort2(int* a, int begin, int end)
{
    int mid = GetMidindex(a, begin, end);
    Swap(&a[mid], &a[end]);
    //坑
    int key = a[end];
    while (begin < end)
    {
        //左边找比key大的
        while (begin < end && a[begin] <= key)
        {
            begin++;
        }
        //将找到的数填在end位置，然后形成新的坑
        a[end] = a[begin];

        //右边找比key小的数
        while (begin < end && a[end] >= key)
        {
            end--;
        }
        //将找到的数填在begin的位置，然后形成新的坑
        a[begin] = a[end];
    }
    //begin和end相遇，循环结束，将key的值填入begin的位置
    a[begin] = key;
    return begin;
}

// 快速排序前后指针法
int PartSort3(int* a, int begin, int end)
{
    int mid = GetMidindex(a, begin, end);
    Swap(&a[mid], &a[end]);
    int key = a[end];
    int keyindex = end;
    int cur = begin;
    int prev = begin - 1;;
    while (cur < end)
    {
        while (a[cur] <= a[keyindex] && ++prev != cur)
        {
            Swap(&a[cur], &a[prev]);
        }

         ++cur;
    }
    
    Swap(&a[++prev], &a[keyindex]);

    return prev;
}

//时间复杂度O(N*log N)
//空间复杂度 O(log N)
void QuickSort(int* a, int left, int right)
{
    assert(a);
    //[left,div-1] , [div+1,right]
    if (left >= right)
        return;

    if ((right - left + 1) > 10)
    {
        //int div = PartSort1(a, left, right);
        //int div = PartSort2(a, left, right);
        int div = PartSort3(a, left, right);

        //PrintArray(a+left, right-left+1);
        //printf("[%d %d] %d [%d %d]", left, div - 1, div, div + 1, right);
        //printf("\n");

        QuickSort(a, left, div - 1);
        QuickSort(a, div + 1, right);
    }

    else
    {
        //小于等于10个数，直接选插入排序,不在递归排序
        InsertSort(a + left, right - left + 1);
    }

}

// 快速排序 非递归实现
//递归改非递归  
//-->1.改循环（斐波拉契数列求解），一些简单递归才能改循环
//-->2.栈模拟存储数据非递归
//非递归：1.提高效率（递归建立栈还是有消耗的，但是对于现代的计算机，这个优化微乎其微，可以忽略不计）
//       2.递归的最大缺陷是，如果栈的深度太深，可能会导致栈溢出，因为系统栈空间一般不大，在M级别
//       数据结构模拟非递归，数据是存储在堆上的，堆是G级别的空间

void QuickSortNonR(int* a, int left, int right)
{
    assert(a);
    //栈来实现快速排序
    Stack st;//定义栈
    StackInit(&st);

    //先入右边，在入左边
    StackPush(&st, right);
    StackPush(&st, left);

    while (!StackEmpty(&st))
    {
        int begin = StackTop(&st);//左边
        StackPop(&st);//先出一个

        int end = StackTop(&st);
        StackPop(&st);

        int div = PartSort1(a, begin, end);

        //先处理左边
        if (begin < div - 1)//左边至少有两个数据
        {
            StackPush(&st, div - 1);
            StackPush(&st, begin);
        }

        //处理右边
        if (end > div + 1)//至少有两个数据
        {
            StackPush(&st, end);
            StackPush(&st, div + 1);
        }
    }
    //销毁栈，防止内存泄漏
    StackDestory(&st);
}

void _MergeArray(int* a, int begin1, int end1, int begin2, int end2, int* tmp)
{
    //递归完了得到两个有序数组
    //归并
    int left = begin1;
    int right=end2;
    int index = begin1;
    while (begin1 <= end1 && begin2 <= end2)
    {
        if (a[begin1] < a[begin2])
        {
            tmp[index] = a[begin1];
            index++;
            begin1++;
        }
        else
        {
            tmp[index] = a[begin2];
            index++;
            begin2++;
        }
    }
    //应该还有一个数组还有剩余元素
    while (begin1 <= end1)
    {
        tmp[index++] = a[begin1++];
    }

    while (begin2 <= end2)
    {
        tmp[index++] = a[begin2++];
    }

    //把归并好的在tmp数组的元素拷贝回原来数组a
    int i = 0;
    for (i = left; i <= right; i++)
    {
        a[i] = tmp[i];
    }
}

void _MergeSort(int* a, int left, int right, int* tmp)
{
    //递归截止条件
    if (left >= right)
    {
        return;
    }
        
    //先递归
    int mid = (left + right) / 2;
    //[left,mid],[mid+1,right]
    _MergeSort(a, left, mid, tmp);
    _MergeSort(a, mid + 1, right, tmp);
    _MergeArray(a, left, mid, mid + 1, right, tmp);
    
}

// 归并排序递归实现
//时间复杂度 O(N*logN)
//空间复杂度 O(N)
void MergeSort(int* a, int n)
{
    assert(a);
    int* tmp = (int*)malloc(sizeof(int) * n);
    if (tmp == NULL)
    {
        printf("申请内存失败\n");
        exit(-1);
    }
    _MergeSort(a, 0, n - 1, tmp);
    free(tmp);//释放内存，防止内存泄漏
}


// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
    assert(a);
    int* tmp = (int*)malloc(sizeof(int) * n);
    int gap = 1;
    while (gap < n)
    {
        int i = 0;
        for (i = 0; i < n; i = i + 2 * gap)
        {
            //使用闭区间
            //[i,i+gap-1],[i+gap,i+2*gap-1]
            int begin1 = i;
            int end1 = i + gap - 1;
            int begin2 = i + gap;
            int end2 = i + 2 * gap - 1;
            //1、合并时只有第一组，第二组不需要合并
            if (begin2 >= n)
            {
                break;
            }
            //2、合并时第二组只有部分数据，需要修改边界值
            if (end2 >= n)
            {
                end2 = n - 1;
            }
            _MergeArray(a, begin1, end1, begin2, end2, tmp);
        }
        gap = gap * 2;
        PrintArray(a, n);
    }
}


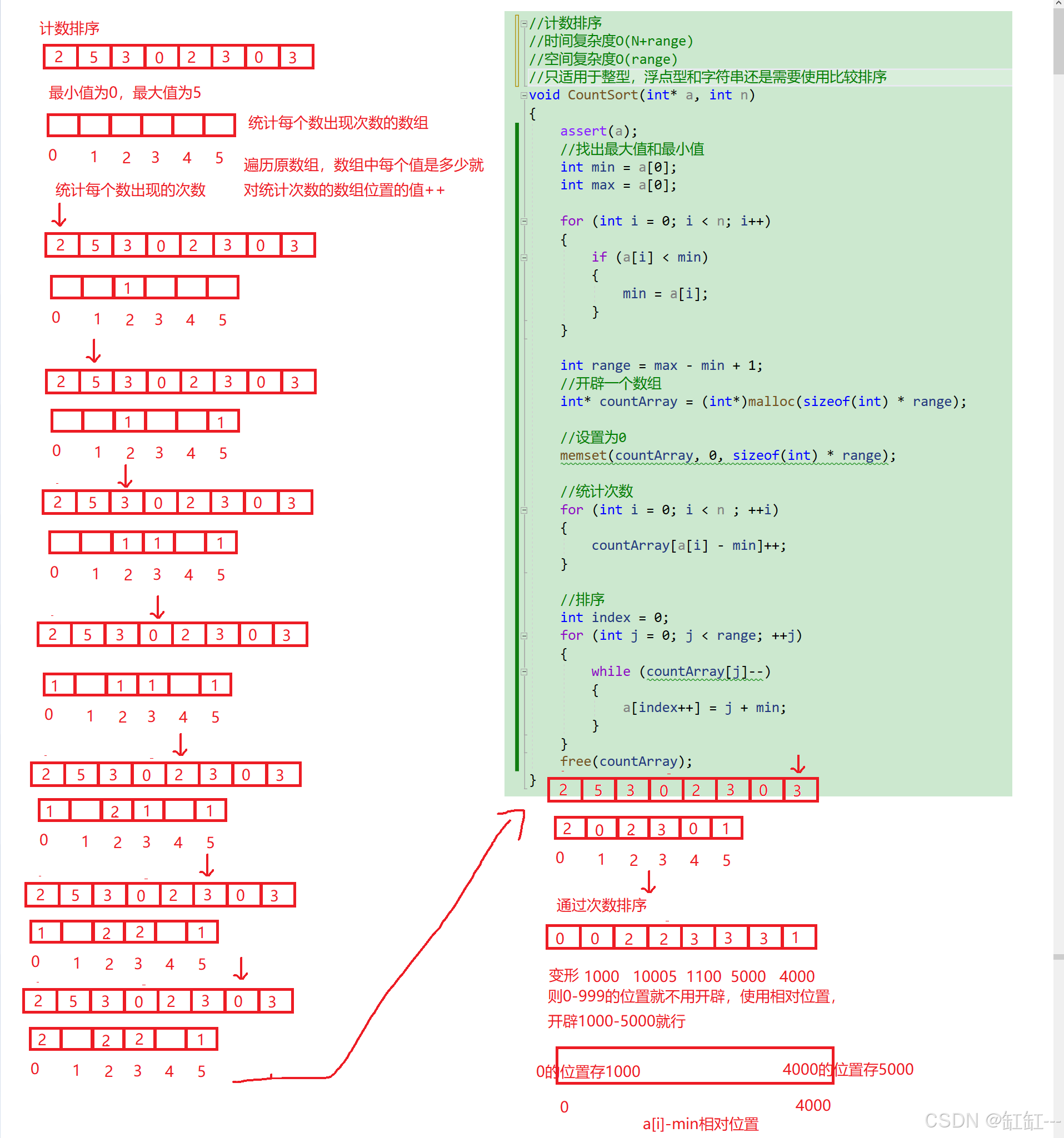
//计数排序
//时间复杂度O(N+range)
//空间复杂度O(range)
//只适用于整型，浮点型和字符串还是需要使用比较排序
void CountSort(int* a, int n)
{
    assert(a);
    //找出最大值和最小值
    int min = a[0];
    int max = a[0];
    
    for (int i = 0; i < n; i++)
    {
        if (a[i] > max)
        {
            max = a[i];
        }

        if (a[i] < min)
        {
            min = a[i];
        }
    }

    int range = max - min + 1;
    //开辟一个数组
    int* countArray = (int*)malloc(sizeof(int) * range);

    //设置为0
    memset(countArray, 0, sizeof(int) * range);

    //统计次数
    for (int i = 0; i < n ; ++i)
    {
        countArray[a[i] - min]++;
    }

    //排序
    int index = 0;
    for (int j = 0; j < range; ++j)
    {
        while (countArray[j]--)
        {
            a[index++] = j + min;
        }
    }
    free(countArray);
}

#define _CRT_SECURE_NO_WARNINGS 1
#include "Sort.h"
#include "Stack.h"

void TestInsertSort()
{
    int a[] = { 2,1,4,3,9,6,4,0,5,8 };
    int sz = sizeof(a) / sizeof(a[0]);
    PrintArray(a, sz);
    InsertSort(a, sz);
    PrintArray(a, sz);
}

TestShellSort()
{
    int a[] = { 20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,0 };
    int sz = sizeof(a) / sizeof(a[0]);
    PrintArray(a, sz);
    ShellSort(a, sz);
    PrintArray(a, sz);
}

void TestSelectSort()
{
    int a[] = { 20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,0 };
    int sz = sizeof(a) / sizeof(a[0]);
    PrintArray(a, sz);
    SelectSort(a, sz);
    PrintArray(a, sz);
}

void TestHeapSort()
{
    int a[] = { 20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,0 };
    int sz = sizeof(a) / sizeof(a[0]);
    PrintArray(a, sz);
    HeapSort(a, sz);
    PrintArray(a, sz);
}

void TestBubbleSort()
{
    int a[] = { 20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,0 };
    int sz = sizeof(a) / sizeof(a[0]);
    PrintArray(a, sz);
    BubbleSort(a, sz);
    PrintArray(a, sz);
}

void TestQuickSort()
{
    //int a[] = { 20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,0 };
    int a[] = { 2,1,4,3,9,6,4,0,5,8 };
    int sz = sizeof(a) / sizeof(a[0]);
    PrintArray(a, sz);
    QuickSort(a, 0,sz-1);
    PrintArray(a, sz);
}

void TestQuickSortNonR()
{
    //int a[] = { 20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,0 };
    int a[] = { 2,1,4,3,9,6,4,0,5,8 };
    int sz = sizeof(a) / sizeof(a[0]);
    PrintArray(a, sz);
    QuickSortNonR(a, 0, sz - 1);
    PrintArray(a, sz);
}

void TestMergeSort()
{
    //int a[] = { 20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,0 };
    int a[] = { 10,6,7,1,3,9,4,2 };
    int sz = sizeof(a) / sizeof(a[0]);
    PrintArray(a, sz);
    MergeSort(a, sz);//不是sz-1，如果是sz-1,会导致最后一个元素没有排到
    PrintArray(a, sz);
}

void TestMergeSortNonR()
{
    //int a[] = { 20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,0 };
    int a[] = { 10,6,7,1,3,9,4 };
    int sz = sizeof(a) / sizeof(a[0]);
    //PrintArray(a, sz);
    MergeSortNonR(a, sz);//不是sz-1，如果是sz-1,会导致最后一个元素没有排到
    //PrintArray(a, sz);
}

void TestCountSort()
{
    //int a[] = { 20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,0 };
    int a[] = { 10,6,7,1,3,9,4 };
    int sz = sizeof(a) / sizeof(a[0]);
    PrintArray(a, sz);
    CountSort(a, sz);//不是sz-1，如果是sz-1,会导致最后一个元素没有排到
    PrintArray(a, sz);
}


void TestOP()
{
    srand(time(0));
    const int N = 100000;

    int* a1 = (int*)malloc(sizeof(int) * N);
    int* a2 = (int*)malloc(sizeof(int) * N);
    int* a3 = (int*)malloc(sizeof(int) * N);
    int* a4 = (int*)malloc(sizeof(int) * N);
    int* a5 = (int*)malloc(sizeof(int) * N);
    int* a6 = (int*)malloc(sizeof(int) * N);
    for (int i = 0; i < N; ++i)
    {
        a1[i] = rand();
        a2[i] = a1[i];
        a3[i] = a1[i];
        a4[i] = a1[i];
        a5[i] = a1[i];
        a6[i] = a1[i];
    }

    int begin1 = clock();
    InsertSort(a1, N);
    int end1 = clock();

    int begin2 = clock();
    ShellSort(a2, N);
    int end2 = clock();

    int begin3 = clock();
    SelectSort(a3, N);
    int end3 = clock();

    int begin4 = clock();
    HeapSort(a4, N);
    int end4 = clock();

    int begin5 = clock();
    BubbleSort(a5, N);
    int end6 = clock();

    int begin7 = clock();
    QuickSort(a5, 0, N-1);
    int end8 = clock();

    int begin9 = clock();
    QuickSortNonR(a5, 0, N - 1);
    int end10 = clock();
    /*int begin5 = clock();
    QuickSort(a5, 0, N - 1);
    int end5 = clock();

    int begin6 = clock();
    MergeSort(a6, N);
    int end6 = clock();*/

    //printf("InsertSort:%d\n", end1 - begin1);
    printf("ShellSort:%d\n", end2 - begin2);
    printf("SelectSort:%d\n", end3 - begin3);
    printf("HeapSort:%d\n", end4 - begin4);
    //printf("BubbleSort:%d\n", end6 - begin5);
    printf("QuickSort:%d\n", end8 - begin7);
    printf("QuickSortNonR:%d\n", end10 - begin9);

    /*printf("QuickSort:%d\n", end5 - begin5);
    printf("MergeSort:%d\n", end6 - begin6);
    free(a1);
    free(a2);
    free(a3);
    free(a4);
    free(a5);
    free(a6);*/
}

int main()
{
    //TestInsertSort();
    //TestShellSort();
    //TestSelectSort();
    //TestHeapSort();

    //TestBubbleSort();
    //TestQuickSort();
    //TestQuickSortNonR();
    //TestMergeSort();
    
    //TestMergeSortNonR();
    //MergeSortFile("Sort.txt");
    TestCountSort();
    
    //TestOP();
    return 0;

}

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
//用数组来实现

//静态的数组
//#define N 10
//struct Stack
//{
//    int _a[N];
//    int _top;
//};

//动态的数组
typedef int STDataType;
typedef struct Stack 
{
    STDataType* _a;
    int _top;//栈顶下标
    int _capacity;
}Stack;

//初始化
void StackInit(Stack* pst);

//销毁
void StackDestory(Stack* pst);

//入栈
void StackPush(Stack* pst, STDataType x);

//出栈
void StackPop(Stack* pst);

//获取数据个数
int StackSize(Stack* pst);

//返回1是空，返回0是非空
int StackEmpty(Stack* pst);

//获取栈顶的数据
STDataType StackTop(Stack* pst);

#define _CRT_SECURE_NO_WARNINGS 1
#include "Stack.h"
//初始化
void StackInit(Stack* pst)
{
    assert(pst);

    //pst->_a = NULL;
    //pst->_top = 0;
    //pst->_capacity = 0;
    pst->_a = (STDataType*)malloc(sizeof(STDataType) * 4);
    pst->_top = 0;
    pst->_capacity = 4;
}

//销毁
void StackDestory(Stack* pst)
{
    assert(pst);
    free(pst->_a);
    pst->_a = NULL;
    pst->_top = 0;
    pst->_capacity = 0;
}

//入栈
void StackPush(Stack* pst, STDataType x)
{
    assert(pst);
    if (pst->_top == pst->_capacity)//满了需要增容
    {
        pst->_capacity *= 2;
        STDataType* tmp = (STDataType*)realloc(pst->_a, pst->_capacity*sizeof(STDataType) );
        if (tmp == NULL)//增容失败
        {
            printf("增容失败\n");
            exit(-1);
        }
        else//将tmp给pst->_a,指向它
        {
            pst->_a = tmp;
        }
    }
    pst->_a[pst->_top] = x;
    pst->_top++;
}

//出栈
void StackPop(Stack* pst)
{
    assert(pst);
    assert(pst->_top > 0);
    --pst->_top;
}

//获取数据个数
int StackSize(Stack* pst)
{
    assert(pst);
    return pst->_top;
}

//返回1是空，返回0是非空
int StackEmpty(Stack* pst)
{
    assert(pst);
    return pst->_top == 0 ? 1 : 0;
}

//获取栈顶的数据
STDataType StackTop(Stack* pst)
{
    assert(pst);
    assert(pst->_top > 0);
    return pst->_a[pst->_top - 1];//pst->_top是元素的个数
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2275104.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

RocketMQ 和 Kafka 有什么区别？

RocketMQ 和 Kafka 有什么区别？

目录 RocketMQ 是什么？ RocketMQ 和 Kafka 的区别 在架构上做减法 简化协调节点 简化分区 Kafka 的底层存储 RocketMQ 的底层存储 简化备份模型 在功能上做加法 消息过滤 支持事务 加入延时队列 加入死信队列 消息回溯 总结 来源：面试官：RocketMQ 和 Kafka 有…
阅读更多...
赛车微型配件订销管理系统(源码+lw+部署文档+讲解)，源码可白嫖!

赛车微型配件订销管理系统(源码+lw+部署文档+讲解)，源码可白嫖!

摘要 赛车微型配件行业通常具有产品多样性、需求不确定性、市场竞争激烈等特点。配件供应商需要根据市场需求及时调整产品结构和库存&#xff0c;同时要把握好供应链管理和销售渠道。传统的赛车微型配件订销管理往往依赖于人工经验和简单的数据分析&#xff0c;效率低下且容易…
阅读更多...
公众号如何通过openid获取unionid

公众号如何通过openid获取unionid

通过接口 https://api.weixin.qq.com/cgi-bin/user/info?access_tokenxxxxxxx&langzh_CN 返回的数据如下&#xff1a; 前提是必须绑定 微信开放平台 token如何获取呢 代码如下&#xff1a; String tokenUrl "https://api.weixin.qq.com/cgi-bin/token"; …
阅读更多...
半导体数据分析： 玩转WM-811K Wafermap 数据集（二） AI 机器学习

半导体数据分析： 玩转WM-811K Wafermap 数据集（二） AI 机器学习

一、数据集回顾 前面我们已经基本了解了WM-811K Wafermap 数据集&#xff0c;并通过几段代码&#xff0c;熟悉了这个数据集的数据结构&#xff0c;这里为了方便各位连续理解&#xff0c;让我们再回顾一下&#xff1a; WM-811K Wafermap 数据集是一个在半导体制造领域广泛使用…
阅读更多...
协同过滤算法私人诊所系统｜Java｜SpringBoot｜VUE｜

协同过滤算法私人诊所系统｜Java｜SpringBoot｜VUE｜

【技术栈】 1⃣️&#xff1a;架构: B/S、MVC 2⃣️&#xff1a;系统环境&#xff1a;Windowsh/Mac 3⃣️&#xff1a;开发环境&#xff1a;IDEA、JDK1.8、Maven、Mysql5.7 4⃣️&#xff1a;技术栈&#xff1a;Java、Mysql、SpringBoot、Mybatis-Plus、VUE、jquery,html 5⃣️…
阅读更多...
Python基于YOLOv8和OpenCV实现车道线和车辆检测

Python基于YOLOv8和OpenCV实现车道线和车辆检测

使用YOLOv8&#xff08;You Only Look Once&#xff09;和OpenCV实现车道线和车辆检测&#xff0c;目标是创建一个可以检测道路上的车道并识别车辆的系统&#xff0c;并估计它们与摄像头的距离。该项目结合了计算机视觉技术和深度学习物体检测。 1、系统主要功能 车道检测&am…
阅读更多...
nexus搭建maven私服

nexus搭建maven私服

说到maven私服每个公司都有&#xff0c;比如我上一篇文章介绍的自定义日志starter&#xff0c;就可以上传到maven私服供大家使用&#xff0c;每次更新只需deploy一下就行&#xff0c;以下就是本人搭建私服的步骤 使用docker安装nexus #拉取镜像 docker pull sonatype/nexus3:…
阅读更多...
MiniMind - 从0训练语言模型

MiniMind - 从0训练语言模型

文章目录 一、关于 MiniMind &#x1f4cc;项目包含 二、&#x1f4cc; Environment三、&#x1f4cc; Quick Start Test四、&#x1f4cc; Quick Start Train0、克隆项目代码1、环境安装2、如果你需要自己训练3、测试模型推理效果 五、&#x1f4cc; Data sources1、分词器&am…
阅读更多...
Postman接口测试基本操作

Postman接口测试基本操作

&#x1f345; 点击文末小卡片 &#xff0c;免费获取软件测试全套资料&#xff0c;资料在手&#xff0c;涨薪更快 Postman-获取验证码 需求&#xff1a;使用Postman访问验证码接口&#xff0c;并查看响应结果。 地址&#xff1a;http://kdtx-test.itheima.net/api/captchaIm…
阅读更多...
基于Python实现的通用小规模搜索引擎

基于Python实现的通用小规模搜索引擎

基于Python实现的通用小规模搜索引擎 1.项目简介 1.1背景 《信息内容安全》网络信息内容获取技术课程项目设计 一个至少能支持10个以上网站的爬虫程序&#xff0c;且支持增量式数据采集;并至少采集10000个实际网页;针对采集回来的网页内容&#xff0c; 能够实现网页文本的分…
阅读更多...
查找路由器的管理后台ip【通用找IP】

查找路由器的管理后台ip【通用找IP】

需求&#xff1a; 刚刚搞了个【小米】路由器&#xff0c;我想进路由的管理后台&#xff0c;提示&#xff1a;安装xx的路由管家&#xff0c;我不想安装 但是无法找到这个管理后台。 而且我是用这个路由作为中继&#xff0c;那么这个路由的ip就会经常更换 尝试通过网上搜索引擎来…
阅读更多...
混合专家模型 (MoE)笔记摘要

混合专家模型 (MoE)笔记摘要

ref&#xff1a; https://huggingface.co/blog/zh/moe#%E4%BB%80%E4%B9%88%E6%98%AF%E6%B7%B7%E5%90%88%E4%B8%93%E5%AE%B6%E6%A8%A1%E5%9E%8B 简短总结 混合专家模型 (MoEs): 与稠密模型相比&#xff0c; 预训练速度更快 与具有相同参数数量的模型相比&#xff0c;具有更快的…
阅读更多...
01 Oracle自学环境搭建

01 Oracle自学环境搭建

1 Oracle12C安装 1.1 下载 官网地址&#xff1a;https://www.oracle.com/ 解压安装包 运行安装程序 1.2 安装 配置安全更新 软件更新 安装选项 系统类 Oracle主目录用户选择 使用现有windows用户&#xff1a;如果选择该项&#xff0c;则需要指定没有管理权限的用户。 创建新Wi…
阅读更多...
【Python】Python与C的区别

【Python】Python与C的区别

文章目录 语句结束符代码块表示变量声明函数定义注释格式Python的标识符数据输入input()函数数据输出print()函数 语句结束符 C 语言 C 语言中每条语句必须以分号;结束。例如&#xff0c;int a 10;、printf("Hello, World!");。分号是语句的一部分&#xff0c;用于…
阅读更多...
安科瑞 Acrel-1000DP 分布式光伏监控系统在工业厂房分布式光伏发电项目中的应用

安科瑞 Acrel-1000DP 分布式光伏监控系统在工业厂房分布式光伏发电项目中的应用

吕梦怡 18706162527 摘 要&#xff1a;常规能源以煤、石油、天然气为主&#xff0c;不仅资源有限&#xff0c;而且会造成严重的大气污染&#xff0c;开发清洁的可再生能源已经成为当今发展的重要任务&#xff0c;“节能优先&#xff0c;效率为本”的分布式发电能源符合社会发…
阅读更多...
逆向 易九批 最新版 爬虫逆向 x-sign ......

逆向 易九批 最新版 爬虫逆向 x-sign ......

声明 本文章中所有内容仅供学习交流&#xff0c;抓包内容、敏感网址、数据接口均已做脱敏处理&#xff0c;严禁用于商业用途和非法用途&#xff0c;否则由此产生的一切后果均与作者无关&#xff0c;若有侵权&#xff0c;请联系我立即删除&#xff01; # 欢迎交流 wjxch1004
阅读更多...
TensorFlow Quantum快速编程（高级篇）

TensorFlow Quantum快速编程（高级篇）

五、实战：量子分类器应用 5.1 数据准备 在实战构建量子分类器时，数据准备是基石环节。选用鸢尾花数据集，这一经典数据集在机器学习领域应用广泛，其涵盖了三种鸢尾花品种的样本，每个样本包含花萼长度、花萼宽度、花瓣长度、花瓣宽度四个特征。鉴于本次构建二分类量子分类…
阅读更多...
maven高级（day15）

maven高级（day15）

Maven 是一款构建和管理 Java 项目的工具 分模块设计与开发 所谓分模块设计&#xff0c;顾名思义指的就是我们在设计一个 Java 项目的时候&#xff0c;将一个 Java 项目拆分成多 个模块进行开发。 分模块设计我们在进行项目设计阶段&#xff0c;就可以将一个大的项目拆分成若干…
阅读更多...
android studio根据包名获取当前安装包信息

android studio根据包名获取当前安装包信息

package com.example.myapplication2;import android.content.Context; import android.content.pm.PackageInfo; import android.content.pm.PackageManager; import android.util.Log;/**** 获取版本信息*/ public class SystemHelper {/*** 获取本地软件版本号*/public stat…
阅读更多...
安卓硬件加速hwui

安卓硬件加速hwui

安卓硬件加速 本文基于安卓11。 从 Android 3.0 (API 级别 11) 开始&#xff0c;Android 2D 渲染管道支持硬件加速&#xff0c;这意味着在 View 的画布上执行的所有绘图操作都使用 GPU。由于启用硬件加速所需的资源增加&#xff0c;你的应用程序将消耗更多内存。 软件绘制&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023