27 Deep Belief Network——深度信念网络

27.1 DBN是什么？

DBN(Deep Belief Network)是由RBM(Restricted Boltzmann Machine)和SBN(Sigmoid Belief Network)两层结构所组成，其图形可以画成如下形式：

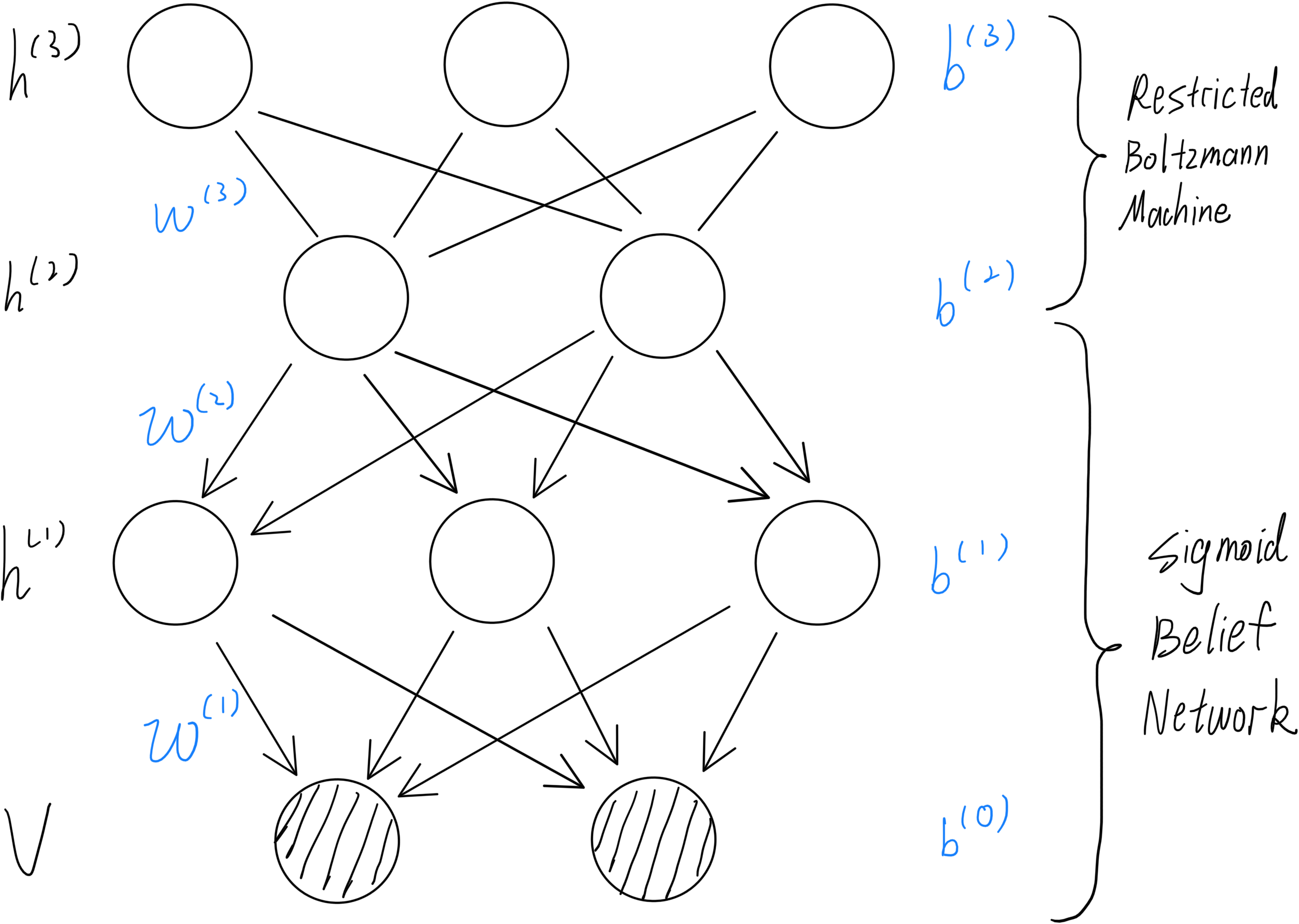
根据其图性质、节点的关联性及分层相互独立的性质，我们可以将联合概率写出来：
$$\begin{array}{rl}P(V,h^{(1)},h^{(2)},h^{(3)})& =P(V|h^{(1)},h^{(2)},h^{(3)})\cdot P(h^{(1)},h^{(2)},h^{(3)})\\ & =P(V|h^{(1)})\cdot P(h^{(1)},h^{(2)},h^{(3)})\\ & =P(V|h^{(1)})\cdot P(h^{(1)}|h^{(2)})\cdot P(h^{(2)},h^{(3)})\\ & =\sum _{i}P(v|h^{(1)})\cdot \sum _{j}P(h_j^{(1)}|h^{(2)})\cdot P(h^{(2)},h^{(3)})\end{array}$$
根据SBN的性质我们可以得到：

1. $P(v|h^{(1)})=sigmoid({w_{:,i}^{(1)}}^T\cdot h^{(1)}+b_i^{(0)})$
2. $P(h_j^{(1)}|h^{(2)})=sigmoid({w_{:,j}^{(2)}}^T\cdot h^{(2)}+b_j^{(1)})$

根据RBM的性质我们可以得到：

• P ( h ( 2 ) , h ( 3 ) ) = 1 Z exp ⁡ { h ( 3 ) T w ( 3 ) h ( 2 ) + h ( 2 ) T b ( 2 ) + h ( 3 ) T b ( 3 ) } P(h^{(2)}, h^{(3)}) = \frac{1}{Z} \exp{\lbrace {h^{(3)}}^T w^{(3)} h^{(2)} + {h^{(2)}}^T b^{(2)} + {h^{(3)}}^T b^{(3)} \rbrace} P(h(2),h(3))=Z1​exp{h(3)Tw(3)h(2)+h(2)Tb(2)+h(3)Tb(3)}

通过以上内容我们就可以得到一个DBN的联合概率公式

27.2 为什么要使用DBN

27.2.1 DBN的思想是怎么来的？

DBN是在RBM的基础上叠加而来，一个基础的RBM应该是如下结构：

我们用该结构求解$P(V)$会通过引入$h^{(1)}$​的方法，再用修正的Gibbs采样的方法（CD-k）进行求解，可以得到：
$$P(V)=\sum _{h^{(1)}}\underset{prior}{\underbrace{P(h^{(1)})}}\underset{fixed}{\underbrace{P(V|h^{(1)})}}$$
其中我们可以将其中的$P(V|h^{(1)})$固定住，并添加一层RBM用于提高prior（提高的原理再下一节），如下图所示：

原先最下层的无向图变为有向图是因为我们的条件是固定住$P(V|h^{(1)})$，所以去掉了从$V$到$h^{(1)}$的方向，如此我们可以叠加很多层。

27.2.2 RBM的叠加可以提高ELBO

如果我们想要将结果的精度再进行提升，我们肯定要将$\log P(V)$中的一部分提高，则我们可以写出的$\log P(V)$ELBO：
$$\begin{array}{rl}\log P(v)& =\log \sum _{h^{(1)}}P(V,h^{(1)})\\ & =\log \sum _{h^{(1)}}q(h^{(1)}|V)\frac{P(V,h^{(1)})}{q(h^{(1)}|V)}\\ & =\log E_{q(h^{(1)}|V)}\left[\frac{P(V,h^{(1)})}{q(h^{(1)}|V)}\right]\\ & \ge E_{q(h^{(1)}|V)}\left[\log \frac{P(V,h^{(1)})}{q(h^{(1)}|V)}\right]\\ & =E_{q(h^{(1)}|V)}\left[\underset{重新建模}{\underbrace{\log P(h^{(1)})}}+\underset{可以通过w_1求解}{\underbrace{\log P(V|h^{(1)})}}-\underset{固定}{\underbrace{\log q(h^{(1)}|V)}}\right]\end{array}$$
根据（以上变换）+（上文所说我们可以固定$P(V|h^{(1)})$​实现叠加RBM——固定表示为定值），可以得到：
$$\begin{array}{rl}\log P(v)& \ge \sum _{h^{(1)}}\underset{fixed}{\underbrace{q(h^{(1)}|V)}}\log P(h^{(1)})+C\end{array}$$
若此时我们对$h^{(1)}$重新建模，在上面加一层$h^{(2)}$，此时$h^{(1)}$就是prior，我们会求得$h^{(1)}$的最大值。通过这种方法我们就可以提高$\log P(V)$的ELBO

27.3 训练方式

通过计算我们已知公式可以写作：
$$\begin{array}{rl}\log P(v)& \ge \sum _{h^{(1)}}q(h^{(1)}|V)\log P(h^{(1)})+C\end{array}$$
其中我们固定的$q(h^{(1)}|V)$可以计算得出：
$$q(h^{(1)}|V)=\prod _{i}q(h_i^{(1)}|V)=\prod _{i}sigmoid(w_{i,:}^{(1)}\cdot v+b_i^{(1)})$$
其中的v就是我们的训练样本。

通过这种方法最后的得到的DBN方便采样：可以在最上层的RBM使用Gibbs采样，再通过SBN对有向图的方法采样下来。