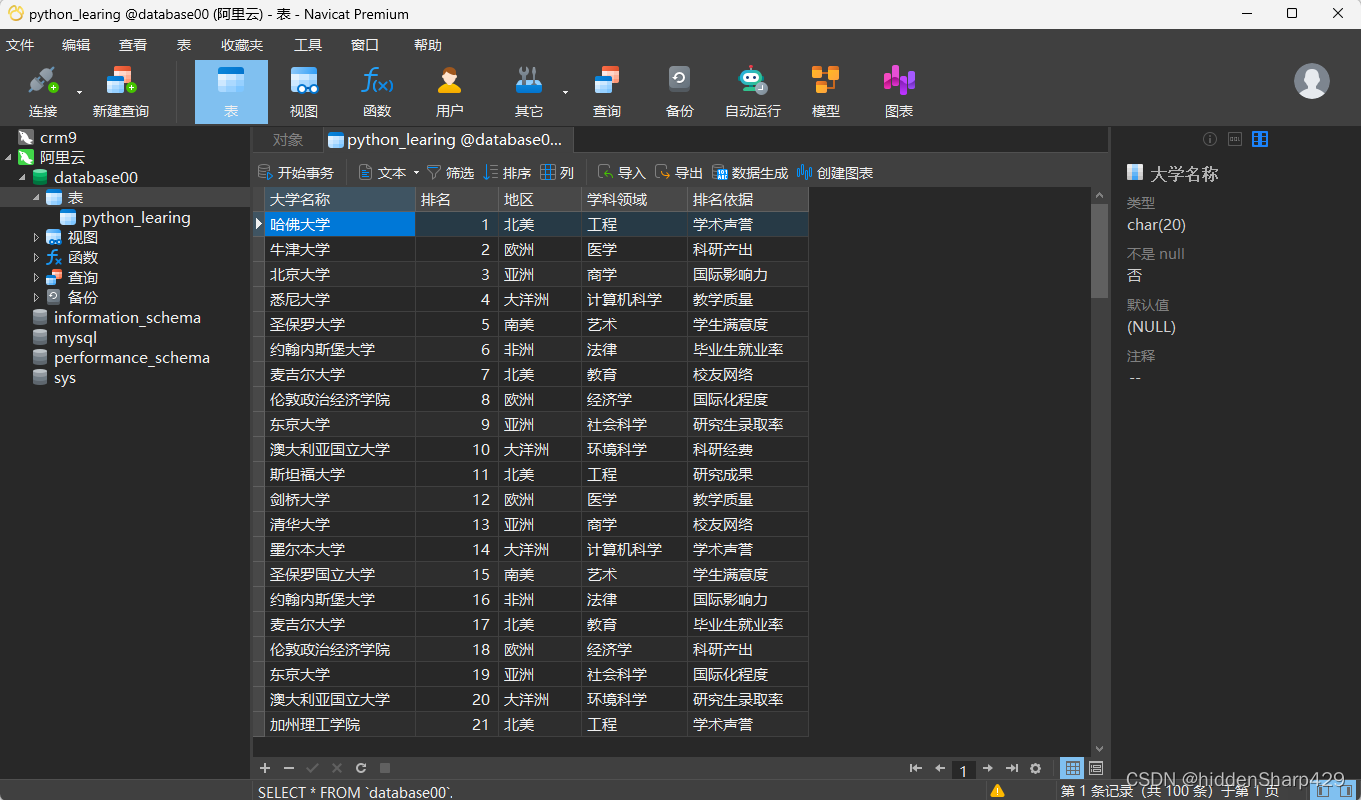
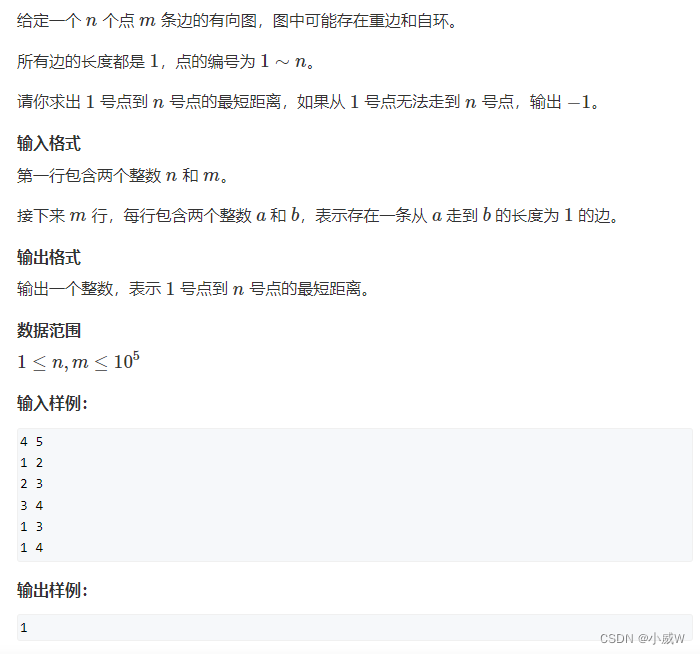
再讲完前面几个数据结构后，下面，我们开始对树进行一个讲解分析

树

引言

树是一种重要的数据结构，在计算机科学中有着广泛的应用。树是由节点和边组
成的非线性数据结构，具有层次结构和递归定义的特点。每个节点可以有多个子
节点，而树的顶部节点称为根节点。树结构可以用于表示层次关系、组织结构、
搜索树、表达式树等。

简单概念

树是n个节点的有限集。n=0时称为空树。在任意一颗非空树中：
1、有且仅有一个特定的称为根的结点
2、当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2 ...，其中每
一个集合又是一棵树，并且称为根的子树。

树的术语

基本

节点（Node）：树的基本单元是节点。每个节点代表一个值，并可以具有指向其
	他节点的链接。每个节点可能具有零个或多个子节点。

根节点（Root）：树的顶部节点称为根节点。它是树中唯一没有父节点的节点。
	从根节点开始，可以通过节点的链接沿着树的层次结构访问其他节点。

子节点（Child）：树中每个节点可以有零个或多个子节点。子节点是直接连接
	到父节点的节点。

父节点（Parent）：一个节点的父节点是指直接连接到该节点的节点。一个节点
	可能有一个父节点。

叶节点（Leaf）：没有子节点的节点称为叶节点或终端节点。它们是树中的末端
	节点。

节点之间的关系

树中的节点之间具有特定的关系。父节点和子节点之间存在一对多的关系。同一
父节点下的子节点之间称为兄弟节点。


层数（Level）：根节点的层数为0，它的子节点为第一层，以此类推。每个节点
	的层数等于它的父节点的层数加1。

高度（Height）：树的高度是根节点到最远叶子节点的最长路径上的边数。树的
	高度反映了树的深度。

子树（Subtree）：树中的任何节点都可以视为树的根，该节点及其所有后代节
	点组成的结构称为子树。

森林（Forest）：森林是多个树的集合。如果一个树的根节点从其他树中删除，
	则这些树的集合称为森林。

树的类型

树的类型有多种形式，每种形式在不同的应用场景下具有特定的优势和用途

常见类型

二叉树（Binary Tree）：二叉树是树的一种特殊形式，每个节点最多有两个子
节点。这两个子节点被称为左子节点和右子节点。二叉树可以为空树（没有任何
节点），也可以是一棵只有根节点的树。

二叉搜索树（Binary Search Tree）：二叉搜索树是一种有序的二叉树，其中
每个节点的左子树上的值都小于该节点的值，而右子树上的值都大于该节点的
值。这种有序性质使得在二叉搜索树中进行查找、插入和删除等操作具有高效
性能。

平衡二叉树（Balanced Binary Tree）：平衡二叉树（也称为AVL树）是一种特
殊的二叉搜索树，其左子树和右子树的高度差不超过1。通过自动平衡树的结构，平衡二叉树可以在查找、插入和删除操作上保持较为均衡的性能。

B树（B-Tree）：B树是一种自平衡的搜索树，用于处理大量的数据和磁盘存储。
B树具有多个子节点和键值对的能力，并在每个节点上维护一个有序的键序列。
B树的特性使得它在数据库索引等应用中具有高效的查找和插入性能。

红黑树（Red-Black Tree）：红黑树是一种自平衡的二叉搜索树，每个节点上有
一个存储的值和一个表示颜色的属性（红色或黑色）。红黑树通过特定的规则保
持平衡，以确保在任何情况下都能保持较为稳定的高度，从而提供高效的查找、
插入和删除操作。

哈夫曼树：哈夫曼树（也称为最优二叉树）是一种用于数据压缩和编码的树结构。
哈夫曼树的构建过程是基于给定的字符频率，先建立最小堆，然后每次从堆中选
取两个频率最小的节点组成新节点，再将新节点放入堆中，直到堆中只剩一个节
点时构建完成。构建完成后，哈夫曼树的前缀编码用于对字符进行压缩和解压缩。
哈夫曼树在图像压缩、文件压缩等领域有广泛的应用。

其他类型

Trie树（Trie Tree）：Trie树（前缀树或字典树）是一种专门用于快速查找字
符串键的树结构。它的特点是将每个键表示为从根节点到叶节点的路径，而共享
的前缀会在树的不同分支上重复使用，这使得Trie树在处理大量字符串键的情况
下非常高效。

AVL树：AVL树是一种自平衡的二叉搜索树，以其发明者的姓氏命名。它在基本的
二叉搜索树的基础上添加了一个平衡条件：每个节点的左子树和右子树的高度差
不超过1。为了保持树的平衡，AVL树会在插入或删除节点时通过旋转操作进行调
整。由于平衡性的保持，AVL树的查找、插入和删除操作的时间复杂度都是
O(log n)。

2-3树（23树）：2-3树（也称为2-3-4树）是一种多叉树，它可以具有2个、3个
或4个子节点。2-3树的特点是每个内部节点可以存储1个或2个键，并且有相应的
子树与之关联。2-3树具有以下性质：所有叶节点在同一层级上，内部节点的键
按非降序排列，并且每个节点的子树范围是按键的范围分割的。2-3树可以自动
调整和重新平衡，以保持树的平衡性。

堆：堆是一种完全二叉树，具有以下两个特性：最大堆（Max Heap）中，每个
节点的值都大于或等于其子节点；最小堆（Min Heap）中，每个节点的值都小
于或等于其子节点。堆是一种非常常用的数据结构，常用于实现优先队列和堆
排序等应用。堆的插入和删除操作的时间复杂度是O(log n)。

树的遍历

树的遍历是指按照一定的次序访问树中的每个节点，常用的遍历方式有3种
先序遍历		中序遍历		后序遍历

还有一种是	层次遍历

常见

先序遍历（Preorder Traversal）：先序遍历以如下方式进行：
	访问根节点。
	递归地先序遍历左子树。
	递归地先序遍历右子树。
	先序遍历的顺序是根节点 → 左子树 → 右子树。先序遍历的应用包括打印
	树的结构、生成前缀表达式和复制树等。

中序遍历（Inorder Traversal）：中序遍历以如下方式进行：
	递归地中序遍历左子树。
	访问根节点。
	递归地中序遍历右子树。
	中序遍历的顺序是左子树 → 根节点 → 右子树。中序遍历的应用包括对树进
		行排序（对于二叉搜索树）和获取有序的节点值。

后序遍历（Postorder Traversal）：后序遍历以如下方式进行：
	递归地后序遍历左子树。
	递归地后序遍历右子树。
	访问根节点。
	后序遍历的顺序是左子树 → 右子树 → 根节点。后序遍历的应用包括计算表
	达式树和释放树等。

另外一种

层序遍历使用队列这种数据结构来实现。具体步骤如下：
	创建一个空队列，并将根节点入队。
	循环执行以下步骤，直到队列为空：
	出队并访问当前节点（打印节点值或存储节点值等）。
	将当前节点的所有子节点按从左到右的顺序入队。
	层序遍历按照从上至下、从左至右的顺序遍历树的每一层。它的输出结果是
		一个按序访问的节点序列。

树的应用
树这种数据结构在计算机科学和软件开发中具有广泛的应用，下面是一些典型的应用场景：

操作系统的文件系统结构中使用树来表示目录结构。
数据库索引使用B树或红黑树等树结构来快速搜索数据。
表达式树（Expression Tree）
对数据结构树的基本概念进行一下详细分析

这些基本概念提供了树数据结构的核心概念和术语。树的结构非常灵活，可以在各种领域和应用中以不同的方式使用。理解这些概念对于正确使用树及其相关算法和数据结构非常重要。

树的应用

文件系统：文件系统常常以树的形式来组织文件和文件夹的层级结构。每个文件
夹（目录）可以包含多个子文件夹或文件，形成一个树的结构，方便进行文件的
组织和查找。

数据库管理系统：数据库中的索引常常使用B树或B+树来实现。这些树结构使得在
大量数据中进行高效的查找、插入和删除成为可能。

编译器：编译器在语法分析阶段使用语法树（也称为解析树）来表示代码的结构。
语法树有助于语法分析和代码优化等编译器任务。

人工智能：决策树是人工智能领域的常用算法，用于根据输入特征进行分类和预
测。决策树算法可以用于人脸识别、推荐系统和自然语言处理等任务。

网络路由：路由器使用路由表（通常是基于树结构的）来决定网络数据包的传输
路径，以实现高效的数据路由。

图形学：在计算机图形学中，场景和对象的层次结构常常表示为树状结构，用于
实现场景图、图层管理和3D模型的组织。

游戏开发：树结构在游戏中有很多应用，如场景图、状态机、行为树和物理碰撞
检测等。

人际关系网络：社交网络的关系可以表示为树状结构，每个人是一个节点，边表
示人与人之间的关系。

补充

实际上，树在许多其他领域也有重要的应用，如编码理论、数据压缩、语言处理
等。树的灵活性和可扩展性使得它成为一种重要的数据结构，在各种领域的问题
求解中发挥着重要作用。

代码实现

import java.util.ArrayList;
import java.util.List;

class TreeNode {
    private int value;
    private List<TreeNode> children;

    public TreeNode(int value) {
        this.value = value;
        this.children = new ArrayList<>();
    }

    public int getValue() {
        return value;
    }

    public List<TreeNode> getChildren() {
        return children;
    }

    public void addChild(TreeNode child) {
        children.add(child);
    }
}

上面代码定义了一个TreeNode类，包含一个值和一个子节点列表。节点的值可以
是任意类型，根据需要进行调整。子节点列表使用一个ArrayList来保存子节点。

这个基本的树实现允许创建一个节点、访问节点的值、获取子节点列表，并允许
添加子节点。

使用示例：

public class Main {
    public static void main(String[] args) {
        TreeNode root = new TreeNode(1);
        TreeNode child1 = new TreeNode(2);
        TreeNode child2 = new TreeNode(3);
        TreeNode grandchild = new TreeNode(4);

        root.addChild(child1);
        root.addChild(child2);
        child2.addChild(grandchild);

        // 访问节点的值
        System.out.println("Root value: " + root.getValue());  // 输出：1
        System.out.println("Child1 value: " + child1.getValue());  // 输出：2
        System.out.println("Grandchild value: " + grandchild.getValue());  // 输出：4

        // 访问子节点列表
        List<TreeNode> children = root.getChildren();
        for (TreeNode child : children) {
            System.out.println("Child value: " + child.getValue());
        }
        // 输出：2, 3

        // 添加子节点
        TreeNode newChild = new TreeNode(5);
        child1.addChild(newChild);
        System.out.println("New child value: " + child1.getChildren().get(1).getValue());  // 输出：5
    }
}

上述示例创建了一个树，包含一个根节点和多个子节点。然后演示了如何访问节
点的值、访问子节点列表，并添加新的子节点。

注意

除此以外，可以根据需要添加更多的功能和方法来扩展树的功能。