392 双指针法很简单

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int i=0;
        for (int j=0; j<t.size() && i<s.size(); j++) {
            if (t[j]==s[i]) {
                i++;
            }
        }
        return i==s.size();
    }
};

用动态规划来写的话 逻辑其实跟1143 1035是一样的 最后返回看dp[s.size()][t.size()]==s.size();

class Solution {
public:
    bool isSubsequence(string s, string t) {
        vector<vector<int>> dp (s.size()+1, vector<int>(t.size()+1, 0));
        for (int i=1; i<=s.size(); i++) {
            for (int j=1; j<=t.size(); j++) {
                if (s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+1;
                else dp[i][j]=dp[i][j-1];
            }
        }
        return dp[s.size()][t.size()]==s.size();
    }
};

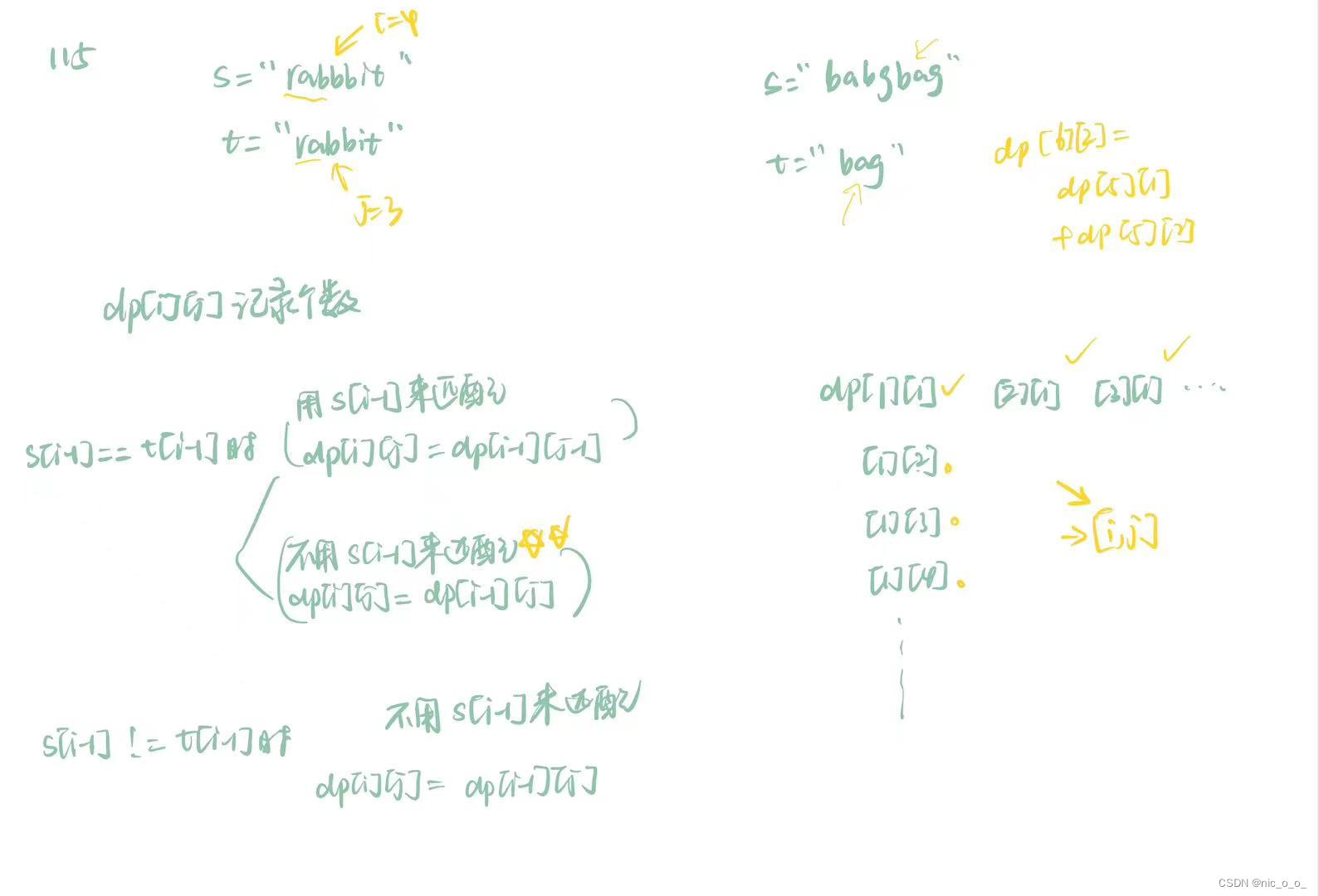
115 这道题写了超久 好在最后自己debug出来了

没想到dp要存的数要用uint64_t来表示

要分用不用s[i-1]来匹配 这个思路很巧妙 根据代码随想录我写了自己的分析

除此之外初始化也很巧妙 可以画一个矩阵图 看每一个是从哪里推算出来的 就知道要初始化的边

t的那边 dp[1][j]一定都是0（j>1时 t的长度大于s的长度）不用特意初始化 跟定义的vector就好 但dp[i][1]=t[0]出现的次数

 

class Solution {
public:
    int numDistinct(string s, string t) {
        vector<vector<uint64_t>> dp (s.size()+1, vector<uint64_t>(t.size()+1,0));

        for (int i=1; i<=s.size(); i++) {
            dp[i][1]=dp[i-1][1];
            if (s[i-1]==t[0]) dp[i][1]+=1;
        }

        for (int i=2; i<=s.size();i++) {
            for (int j=2; j<=t.size(); j++) {
                if (s[i-1]==t[j-1]) {
                    dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
                    //cout<<"dp["<<i-1<<"]["<<j-1<<"]="<<dp[i-1][j-1]<<" "<<"dp["<<i-1<<"]["<<j<<"]="<<dp[i-1][j]<<endl;
                    //cout<<"dp["<<i<<"]["<<j<<"]=dp["<<i-1<<"]["<<j-1<<"]+dp["<<i-1<<"]["<<j<<"]="<<dp[i][j]<<endl;
                }
                else {
                    dp[i][j]=dp[i-1][j];
                    //cout<<"dp["<<i-1<<"]["<<j<<"]="<<dp[i-1][j]<<endl;
                    //cout<<"dp["<<i<<"]["<<j<<"]=dp["<<i-1<<"]["<<j<<"]="<<dp[i][j]<<endl;
                }
                //cout<<endl;
            }
        }
        return dp[s.size()][t.size()];
    }
};