一、说明
对于统计模式识别,需要从基本的检验入手进行学习掌握,本篇是对统计中存在问题的探讨:如果两个分布有重叠该怎么做。具体的统计学原理,将在本人专栏中系统阐述。
二、几个重要概念
2.1 什么是假设检验
假设检验是一种统计学方法,用于确定两个或多个样本之间是否存在差异或者是否符合某种假设。它通常涉及两个假设,一个是原假设(null hypothesis),另一个是备择假设(alternative hypothesis)。原假设是一种默认假设,认为样本之间没有差异或者不符合某种假设;备择假设则认为样本之间存在差异或者符合某种假设。通过统计技术计算样本的差异程度和假设的置信度,可以得出是否拒绝原假设的结论,从而判断样本是否具有统计学意义。

2.2 什么是置信区间
置信区间是指通过样本数据估计总体参数时,给出一个区间,该区间内包含我们对总体参数真值的估计值的置信程度。换句话说,它是对总体参数一个区间估计,而不是一个确定的值。通常情况下,置信区间由一个下限和一个上限组成,并且由置信水平和样本统计量确定。例如,如果置信水平为95%,则置信区间为从样本统计量下侧的5%到上侧的5%。换句话说,有95%的置信度,真实总体参数的值位于置信区间中。
执行假设检验时,可以使用 p 值或置信区间来确定结果是否具有统计显著性。
我最近遇到一种情况,讨论是关于确定两个样本的统计显著性或两个样本之间的差异。结论是对两个样本进行测试导致更保守的结果。即使两个样本之间的差异显示了统计显著性,但在某些情况下,两个样本检验不会显示统计显著性。
我想知道为什么会这样,并被这篇文章删除了。这是我用一些代码模仿帖子上的讨论。
三、具有重叠置信区间的统计显著性
3.1 当方差接近时
当两组统计数据分布距离太近,用假设检验已经无法说明其显著性,此时用ME模型可以解决,本文仅限于说明两组统计数据,显著性差异不明显情况。
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import matplotlib.style as style
style.use('fivethirtyeight')
m1 = 9
m2 = 17
sd1 = 2.5
sd2 = 2.5
ci1 = stats.norm.interval(0.95, loc=m1, scale=sd1)
ci2 = stats.norm.interval(0.95, loc=m2, scale=sd2)
def returnNormalY(x, mu, sd):
return 1/(sd * np.sqrt(2 * np.pi)) * np.exp(-(x - mu)**2 / (2 * sd**2))
# Generate Data for Plot
# Fill Section
x1 = np.linspace(ci1[0], ci1[1], 1000)
y1 = returnNormalY(x1, m1, sd1)
x2 = np.linspace(ci2[0], ci2[1], 1000)
y2 = returnNormalY(x2, m2, sd2)
# Line Section
x1_line = np.linspace(0, 17)
y1_line = returnNormalY(x1_line, m1, sd1)
x2_line = np.linspace(9, 25)
y2_line = returnNormalY(x2_line, m2, sd2)
# Generate Plot
fig, ax = plt.subplots()
ax.plot(x1_line, y1_line)
ax.plot(x2_line, y2_line)
ax.fill_between(x1, y1, alpha=0.3)
ax.fill_between(x2, y2, alpha=0.3)
# Plot Editing
fig.set_size_inches(8, 6, forward=False)
ax.set_yticklabels([])
plt.title("Overlapping Confidence Intervals")
plt.show()
从上图中可以看出,两个样本的 95% 置信区间是重叠的。仅此图就应表明缺乏统计显著性。然而
3.2 当方差相异时,具有样本差异的统计显著性
# Generate Data for Difference
m3 = m2 - m1
sd3 = np.sqrt(np.square(sd1)/1 + np.square(sd2)/1)
ci3 = stats.norm.interval(0.95, loc=m3, scale=sd3)
# Fill Section
x3 = np.linspace(ci3[0], ci3[1], 1000)
y3 = returnNormalY(x3, m3, sd3)
# Line Section
x3_line = np.linspace(-1, 25)
y3_line = returnNormalY(x3_line, m3, sd3)
# Generate Plot
fig, ax = plt.subplots()
ax.plot(x3_line, y3_line, 'y')
ax.fill_between(x1, y1, alpha=0.1)
ax.fill_between(x2, y2, alpha=0.1)
ax.fill_between(x3, y3, alpha=0.4)
# Plot Editing
fig.set_size_inches(8, 6, forward=False)
ax.set_yticklabels([])
plt.title("Confidence Interval of Difference")
plt.show()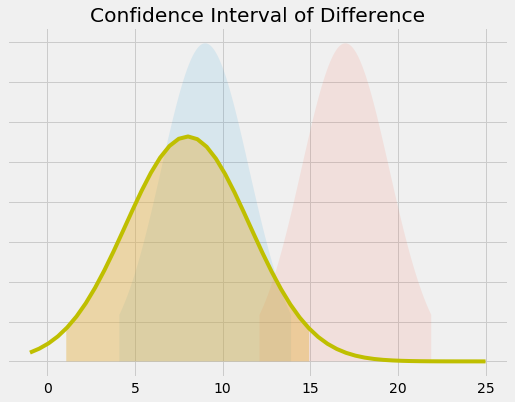
两个样本之差的 95% 置信区间显示出统计学意义。这背后的原因是在上述代码的第 3 行。差值上的标准差不是两个标准差的总和。他们加正交(取平方和的平方根)。
看看这个例子,前面关于两个样本导致保守结果的说法似乎是有效的。
四、总结
- 重叠置信区间缺乏统计显著性
- 两个样本之间方差有差异的置信区间对统计显著性有更宽松的批准
- 当不包括 0 时,单个置信区间有效


![get请求传入[ ]这类字符 返回400错误解决](https://img-blog.csdnimg.cn/8b5f56b7b1f7422583923489d9685640.png)