最低有效位（Least Significant Bit，LSB）指的是一个二进制数中的第 0 位（即最低位）。
最低有效位信息隐藏指的是，将一个需要隐藏的二值图像信息嵌入载体图像的最低有效位，即将载体图像的最低有效位层替换为当前需要隐藏的二值图像，从而实现将二值图像隐藏的目的。
由于二值图像处于载体图像的最低有效位上，所以对于载体图像的影响非常不明显，其具有较高的隐蔽性。

这种信息隐藏也被称为数字水印，通过该方式可以实现信息隐藏、版权认证、身份认证等功能。
例如，如果嵌入载体图像内的信息是秘密信息，就实现了信息隐藏；如果嵌入载体图像内的信息是版权信息，就能够实现版权认证；如果嵌入载体图像内的信息是身份信息，就可以实现数字签名，等等。所以，被嵌入载体图像内的信息也被称为数字水印信息。
数字水印信息可以是文本、视频、音频等多种形式

内容有点多，要是我看到直接就蒙圈了，一点点看，一天看一些理解下也可以

原理

从位平面的角度考虑，数字水印的处理过程分为下面两步。
 嵌入过程：将载体图像的第 0 个位平面替换为数字水印信息（一幅二值图像）。
 提取过程：将载体图像的最低有效位所构成的第 0 个位平面提取出来，得到数字水印信
息。

1．嵌入过程

嵌入过程是将数字水印嵌入载体图像的过程。该过程实现的是，将载体图像的最低有效位
用数字水印信息替换，得到包含水印信息的载体图像。
为了处理和说明起来方便，这里以原始图像为灰度图像、水印图像为二值图像为例。在实际处理中，原始图像、水印图像均可以为彩色图像，这时需要先对它们进行通道分解、图层分解，后续的处理方法与在灰度图像内嵌入二值水印图像的处理方法相同。

（1）原始载体图像预处理
为了便于理解，我们将载体图像处理为二进制形式，并标记出最低有效位。
例如，有灰度图像 O 作为载体图像，图像 O 中各个像素点的像素值为：

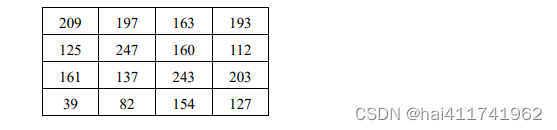
其对应的二进制表示 OB 为：

为了更直观，我们用下画线将图像的二进制表示 OB 的最低有效位标记出来了。被标记的值构成了载体图像 O 的第 0 个位平面，即“最低有效位”位平面 OBLSB，其具体值为：

（2）水印图像处理
为了方便处理，在嵌入水印前，需要将水印信息处理为二值图像。比较典型的情况是将灰度二值水印信息进行阈值处理，将其处理为二进制二值水印信息。
在灰度二值图像中，像素值只有 0 和 255 两种类型值，分别用来表示黑色和白色。可以将其中的 255 转换为 1，这样就得到了一幅二进制二值图像。在二进制二值图像中，仅仅用一个比特位表示一个像素值，像素值只有 0 和 1 两种可能值。经过上述处理，能够更方便地实现水印嵌入。
例如，有灰度二值水印图像 W，其像素值为

不能直接将上述水印图像嵌入载体图像内，需要将其转换为二进制二值水印图像，以方便嵌入。通过阈值处理，得到二进制二值水印图像 WB，其具体值为：

(在OpenCV中，阈值处理是一种常用的图像处理技术，它可以将图像中的像素值分成两个或多个区域，从而实现图像的分割和二值化)

经过处理后，二进制二值水印信息正好可以嵌入载体图像的最低有效位上。

（3）嵌入水印
将载体图像的最低有效位替换为二进制水印图像，完成水印的嵌入。
例如，将载体图像 OB 的最低有效位用水印信息 WB 替换，得到含水印载体图像的二进制形式 WOB，其具体值为：

将 WOB 转为十进制形式，即得到含水印载体图像的十进制值形式 WO，其值为：

由于信息的最低有效位对值的大小影响有限，因此，将载体图像最低有效位的值用水印信息替换后，载体图像像素的值并没有发生太大变化，人眼不足以看出区别，水印具有较高的隐蔽性。

提取水印

提取过程是指将水印信息从包含水印信息的载体图像内提取出来的过程。提取水印时，先
将含水印载体图像的像素值转换为二进制形式，然后从其最低有效位提取出水印信息即可。因
此，可以通过提取含水印载体图像的“最低有效位”位平面的方式来得到水印信息。
例如，有包含水印信息的载体图像 WOE，其具体值为：

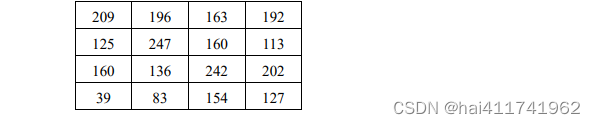
将含水印信息的载体图像 WOE 转换为二进制形式 WOEB，得到：

提取 WOEB 的最低有效位信息（“最低有效位”位平面，即第 0 个位平面），即可得到水印信息 WE，其值为：

根据需要，决定是否进行阈值处理。如有必要，则通过阈值处理将其中值为 1 的像素点转换为 255，得到含有 0 和 255 两个值的二值水印图像 WET，具体值为：

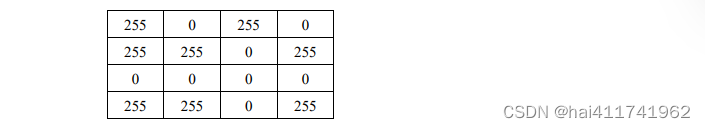
通过上述例题可以发现，经过上述处理后，得到的水印图像 WET 与嵌入的水印图像 W 是一致的。
为了便于理解，这里仅介绍了原始载体图像为灰度图像的情况，在实际中可以根据需要在多个通道内嵌入相同的水印（提高鲁棒性，即使部分水印丢失，也能提取出完整水印信息），
或在各个不同的通道内嵌入不同的水印（提高嵌入容量）。在彩色图像的多个通道内嵌入水印的方法，与在灰度图像内嵌入水印的方法相同。

实现方法

最低有效位水印的实现包含嵌入过程和提取过程，下面对具体的实现方法进行简单介绍。
1．嵌入过程
嵌入过程完成的操作是，将数字水印信息嵌入载体图像内，其主要步骤如下。

（1）载体图像预处理
读取原始载体图像，并获取载体图像的行数 M 和列数 N。
例如，有原始载体图像 O，其像素值为：

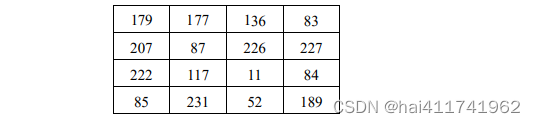
将其对应的二进制形式记为 OB，其具体值为：

（2）建立提取矩阵
建立一个 M×N 大小、元素值均为 254 的提取矩阵（数组），用来提取载体图像的高七位。
例如，按照原始图像 O 的大小建立一个 4×4 大小、元素值均为 254 的数组 T，其具体为：

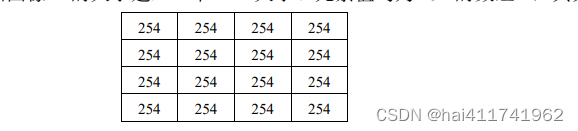
T 所对应的二进制形式记为 TB，其具体值为：

（3）保留载体图像的高七位，将最低位置零
为了实现该操作，需要将载体图像与元素值均为 254 的提取矩阵进行按位与运算。
将一个值在[0,255]之间的像素值 P 与数值 254 进行按位与运算，则会将像素值 P 的最低有
效位置零，只保留其高七位。例如：
 某个像素 Pa 的像素值为 217，将像素 Pa 与 254 进行按位与运算，则像素 Pa 的二进制
像素值高七位保持不变，最低有效位被清零。像素 Pa 的最低有效位上原来的值是 1，
因此，经过运算后像素 Pa 的像素值 217 减少 1，变为 216。
 某个像素 Pb 的像素值为 216，将像素 Pb 与 254 进行按位与运算，则像素 Pb 的二进制
像素值高七位保持不变，最低有效位被清零。像素 Pb 的最低有效位上原来的值就是 0，
因此在运算后像素 Pb 的像素值仍然是 216。
该运算示例具体如表 3-17 所示。

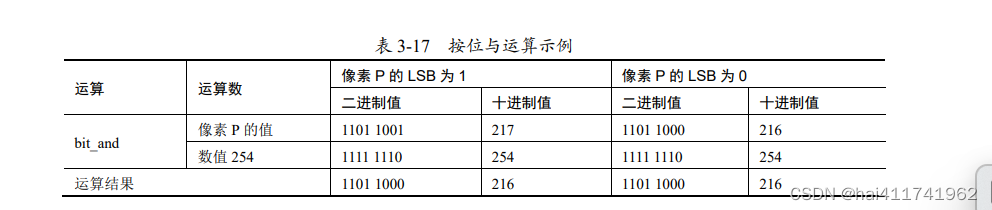
表中的 LSB 表示 Least Significant Bit，即最低有效位。
根据以上分析，将载体图像与元素值均为 254 的提取矩阵进行按位与运算，相当于将载体
图像内的每个像素值均与值 254 进行按位与运算。这样就实现了将整个图像内所有像素二进制值的高七位保留、最低位置零。

例如，将原始载体图像 OB 与元素值均为 254 的提取矩阵 TB 进行按位与运算，则 OB 的
高七位保持不变，而最低有效位被置零。即实现了只保留 OB 的高七位，得到 OBH，其具体值为：

（4）水印图像处理
有些情况下需要对水印进行简单处理。例如，当水印图像为 8 位灰度图的二值图像时，就需要将其转换为二进制二值图像，以方便将其嵌入载体图像的最低位。
例如，有一幅灰度二值水印图像 W，具体值为：

我们将其中的像素值 255 转换为像素值 1，以方便嵌入载体图像。该灰度二值图像对应的二进制图像为 WT，其值具体为：

其对应的 8 位二进制形式 WTB 为：

（5）嵌入水印
将原始载体图像进行“保留高七位、最低位置零”的操作后，我们得到一幅新的图像，将新图像与水印图像进行按位或运算，就能实现将水印信息嵌入原始载体图像内的效果。

将一个最低有效位（LSB）为 0 的数值 A 与一个只有一位的二进制值 B（单位二进制值）进行按位或运算时：

 当该二进制值 B 为 0 时，按位或运算的结果是 0，数值 A 的值保持不变。由于 B 的值为 0，因此，如果从最低有效位的角度理解，可以理解为数值 A 的最低有效位被替换为单位二进制值 B 的值，也可以理解为将单位二进制值 B 嵌入数值 A 内（的最低有效位上）。

 当该二进制值 B 为 1 时，按位或运算的结果是 1，数值 A 的高七位保持变，而最低有效位变为 1。因此，如果从最低有效位的角度理解，可以理解为数值 A 的最低有效位被替换为单位二进制值 B 的值，也可以理解为将单位二进制值 B 嵌入数值 A 内（的最低有效位上）。

总结来看，将一个最低有效位（LSB）为 0 的数值 A 与一个单位二进制值 B 进行按位或运算，相当于用该单位二进制值 B 替换原始数值 A 的最低有效位，即可以实现将单位二进制值 B嵌入数值 A 的最低有效位上。

例如，将最低有效位是 0 的数字 216 分别与单位二进制值 0 和单位二进制值 1 进行按位或
运算，如表 3-18 所示。

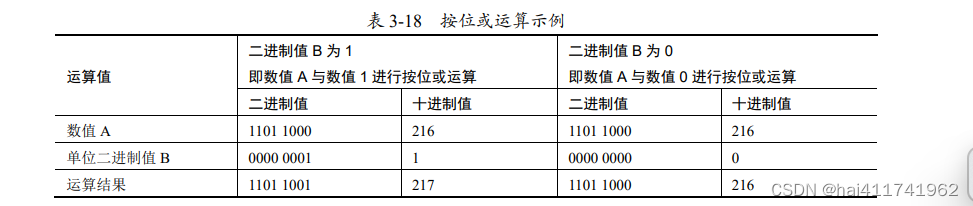
可以推断，如果将二进制二值水印图像（单位二进制值的水印图像）与最低有效位被置零
后得到的原始载体图像进行按位或运算，就可以实现将水印信息嵌入原始载体图像内。
因此，将水印信息 WB 与原始载体图像 O 的高七位图像 OBH 进行按位或运算，即完成将
水印信息嵌入原始载体图像 O 的 OBH 内，就可以得到含水印载体图像 WO。WO 的具体值为：

（6）显示图像
完成上述处理后，分别显示原始载体图像、水印图像、含水印图像。水印嵌入过程的流程图如图 3-12 所示。

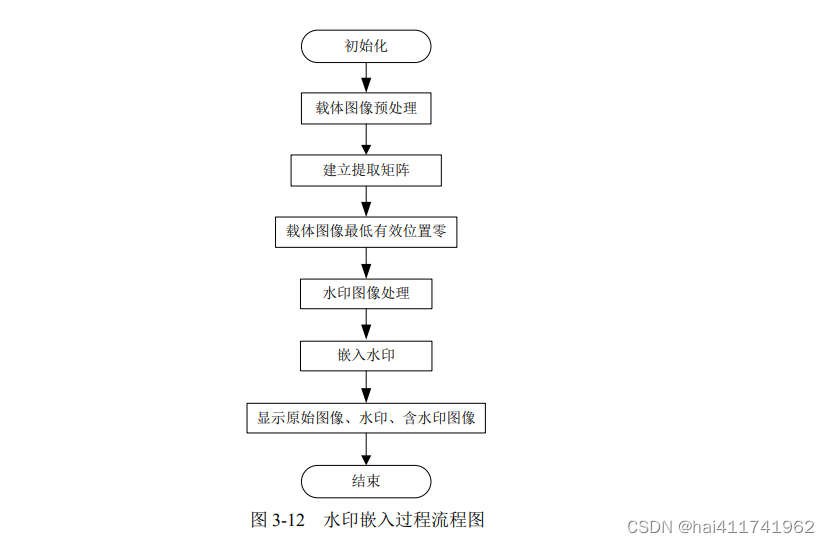
2．提取过程

提取过程将完成数字水印的提取，具体步骤如下。
（1）含水印载体图像处理
读取包含水印的载体图像，获取含水印载体图像的大小 M×N。
例如，读取含水印载体图像 WO，获取其大小为 4×4。WO 的具体值为：

（2）建立提取矩阵
定义一个与含水印载体图像等大小的值为 1 的矩阵（数组）作为提取矩阵。
例如，定义一个大小为 4×4 的矩阵作为提取矩阵，使其中的值均为 1，将该矩阵标记为 T1：

其对应的 8 位二进制形式 Te 为：

（3）提取水印信息
将含水印载体图像与提取矩阵进行按位与运算，提取水印信息。
将一个值在[0, 255]之间的像素 P 与数值 1 进行按位与运算，则会将像素 P 的像素值的高七
位置零，只保留像素 P 的最低有效位（LSB）。

下面分别以像素 P 的最低有效位为 0 和 1 为例进行说明。
 如果像素 P 的最低有效位为 1，则会得到值 1。
例如，某像素 Pa 的值为 217，将其与数值 1 进行按位与运算，则 Pa 的高七位被置零，
只有其最低有效位被保留，得到值 1。
 如果像素 P 的最低有效位为 0，则会得到值 0。
例如，某像素 Pb 的值为 216，将其与数值 1 进行按位与运算，则 Pb 的高七位被置零，
只有其最低有效位被保留，得到值 0。

该实例的具体计算如表 3-19 所示。

基于上述规则，针对图像内的每个像素，将其与数值 1 进行按位与操作，即可将图像的最
低有效位提取出来。
因此，可以将含水印载体图像与元素值均为 1 的提取矩阵进行按位与运算，以实现提取水
印信息。

例如，含水印载体图像 WO 为：

将含水印图像 WO 与提取矩阵 Te 进行按位与运算，即可得到二进制值水印信息 We，其值为：

将提取出来的二进制水印信息 We 进行阈值处理，将其中值为 1 的像素值调整为 255，以
便显示。阈值处理后，得到二值水印图像 WG，具体值为：

（4）计算去除水印后的载体图像
有时需要删除包含在水印载体图像内的水印信息。通过将含水印载体图像的最低有效位置
零，即可实现删除水印信息。
建立一个大小为 4×4、元素值均为 254 的矩阵，将该矩阵标记为 T2，其具体为：

将上述 T2 所对应的二进制形式记为 TB，其具体值为：

通过将含水印载体图像 WO 与 TB 进行按位与运算，即可将载体图像 WO 的最低有效位置
零，得到删除水印信息的载体图像 ODW。该操作的具体实现原理及过程，与水印嵌入时对原
始图像的最低有效位置零操作是类似的。

（5）显示图像
根据需要，分别显示提取出来的水印图像 WG、删除水印信息的载体图像 ODW。
水印提取过程的流程图如图 3-13 所示。

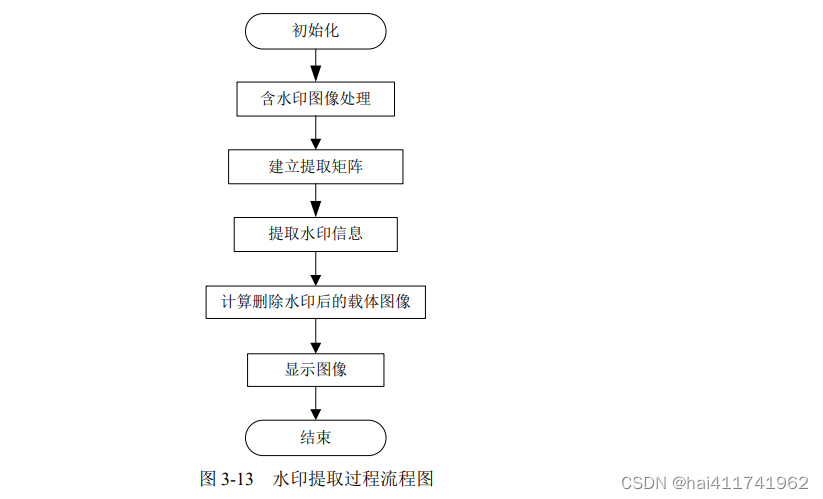
就是说，也可以通过让含水印载体图像像素值对 2 取模的方式，来获取最低有效位水印。