前言
1、推荐在线进制转换器:(都还不错)
在线进制转换 | 进制转换器 — 在线工具 (sojson.com)
在线进制转换器 | 菜鸟工具 (runoob.com)
在线进制转换 - 码工具 (matools.com)
2、进位计数法
(1)二进制:基数为 2,只有 0 和 1 两种数字符号,计数 “ 逢二进一 ” ,任意数位的权为 , i 为所在位数。
(2)八进制:基数为 8,有 0 - 7 共八个不同的数字符号,计数 “ 逢八进一 ” 。(二进制中的 3 位数码编为一组即一位八进制数码)
(3)十进制:基数为 10,计数 “ 逢十进一 ”。
(4)十六进制:基数为 16,计数 “ 逢十六进一 ”,每个数位可取 0-9、A、B、C、D、E、F 中的任意一个,其中 A - F 分别表示 10 - 15。(二进制中的 4 位数码编为一组即一位十六进制数码)
一、二进制转八进制(2 -> 8)
1、二进制只有整数部分
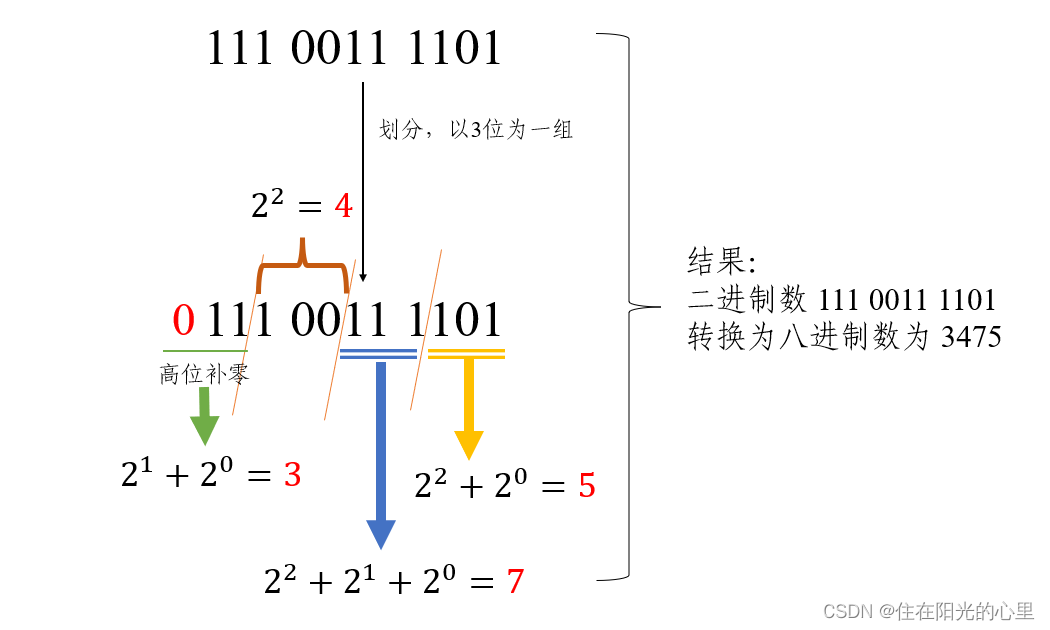
做法:将一串二进制数分为 3 位(八进制)一组,在数的最左边(高位)可根据需要加 “ 0 ” 补齐。
即 “ 整数部分,高位补零 ”
例1:将二进制数 111 0011 1101 转换为八进制数。
解:如下图
2、二进制包含整数部分和小数部分
做法:对于整数部分(小数点往左数),将一串二进制数分为 3 位(八进制)一组,在数的最左边(高位)可根据需要加 “ 0 ” 补齐。
对于小数部分(小数点往右数),将一串二进制数分为 3 位(八进制)一组,在数的最右边(低位)可根据需要加 “ 0 ” 补齐。
即 “ 整数部分,高位补零。小数部分,低位补零 ”
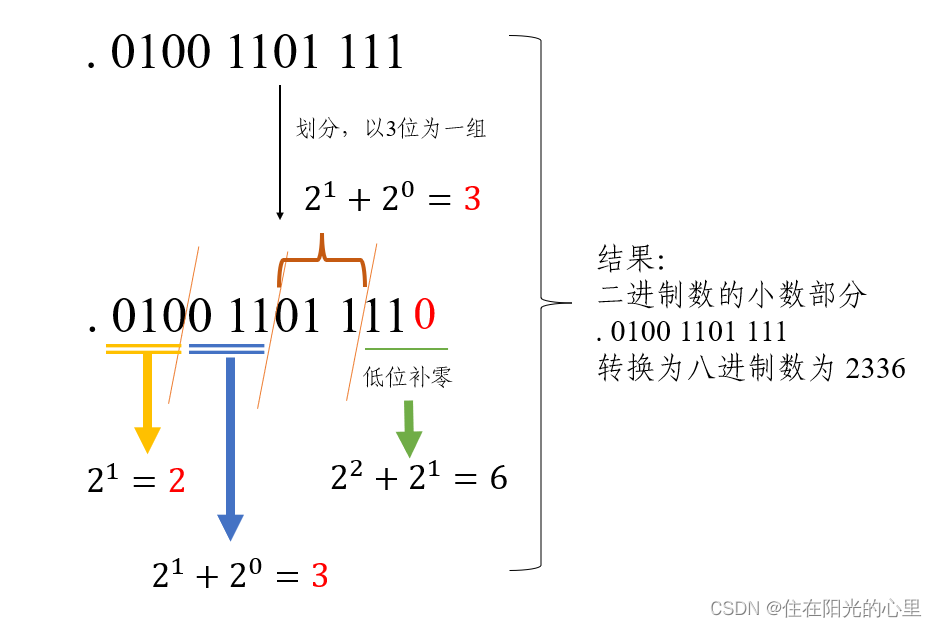
例2:将二进制数 111 0011 1101 . 0100 1101 111 转换为八进制数。
解:整数部分如同例1解法,下图为针对小数部分解法
所以二进制数 111 0011 1101 . 0100 1101 111 转换为八进制数为 3475.2336
二、二进制转十六进制(2 -> 16)
做法:二进制数转十六进制与转八进制类似。
对于整数部分(小数点往左数),将一串二进制数分为 4 位(十六进制)一组,在数的最左边(高位)可根据需要加 “ 0 ” 补齐。
对于小数部分(小数点往右数),将一串二进制数分为 4 位(十六进制)一组,在数的最右边(低位)可根据需要加 “ 0 ” 补齐。
例3:将二进制数 111 0011 1101 . 0100 1101 111 转换为十六进制数。
解:如下图
三、任意进制数转换为十进制数(R -> 10)
按权展开相加法:将任意进制数的各位数码与它们的权值相乘,再把乘积相加,即得一个十进制数。
例4:将二进制数 1101.11 转换为十进制数。
解:如下图
例5:将八进制数 371 转换为十进制数。
解:如下图
四、十进制数转换为任意进制数(10 -> R)
(一)十进制数转换为二进制数
1、十进制数为整数
除基取余法:整数部分除基取余,最先取得的余数为数的最低位,最后取得的余数为数的最高位,商为0时结束。
即 “ 除基取余,先余为低,后余为高 ”
2、十进制数包含整数和小数
乘基取整法:小数部分乘基取整,最先取得的整数为数的最高位,最后取得的整数为数的最低位,乘积为 1.0 (或满足精度要求)时结束。
即 “ 乘基取余,先余为高,后余为低 ”
例6:将十进制数 123.6875 转换为二进制数。
解:如下图
所以,十进制数 123.6875 转换为二进制数为 1111011.1011
(二)十进制数转换为八进制数
例7:将十进制数 123.6875 转换为八进制数。
解:由例 6 可知,十进制数 123.6875 转换为二进制数为 1111011.1011
所以,可用二进制转八进制的方法,即“ 整数部分,高位补零。小数部分,低位补零 ”。
所以,十进制数 123.6875 转换为八进制数为 173.54