【每日一题】1691. 堆叠长方体的最大高度

题目描述

给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [widthi, lengthi, heighti]（下标从 0 开始）。请你从 cuboids 选出一个 子集 ，并将它们堆叠起来。
如果 widthi <= widthj 且 lengthi <= lengthj 且 heighti <= heightj ，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。
返回 堆叠长方体 cuboids 可以得到的 最大高度 。

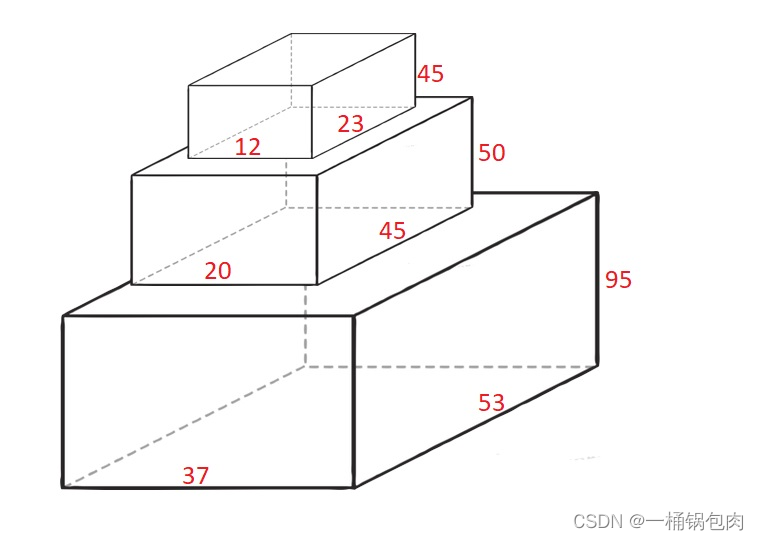
输入：cuboids = [[50,45,20],[95,37,53],[45,23,12]]
输出：190
解释：
第 1 个长方体放在底部，53x37 的一面朝下，高度为 95 。
第 0 个长方体放在中间，45x20 的一面朝下，高度为 50 。
第 2 个长方体放在上面，23x12 的一面朝下，高度为 45 。
总高度是 95 + 50 + 45 = 190 。

题目解析

【贪心】：该题需要若干个长方体堆叠在一起得到的高度最高，直观来说，将长方体的最长边作为高，可将高度最高。
【排序】：题目中有比较的要求，所以首先要对长方体进行排序。可以从两个维度进行排序。分别是单个长方体（按照长、宽、高的长度排序），以及多个长方体的比较。
【动态规划】：设dp[i]为将第i个长方体作为最下层的长方体时，所能达到的最大高度。则状态转移方程为
$$dp[i]=ma{x}_{w_j<=w_i,h_j<=h_i,h_j<=h_i}dp[j]+h[i]$$

class Solution {
    public int maxHeight(int[][] cuboids) {
        int num = cuboids.length;
        // 对每个长方体进行排序
        for(int[] v : cuboids){
            Arrays.sort(v);
        }
        // 多个长方体排序
        Arrays.sort(cuboids, (o1, o2) -> ((o1[0] + o1[1] + o1[2]) - (o2[0] + o2[1] + o2[2])));
        int ans = 0;
        //dp
        int[] dp = new int[num];
        for(int i = 0; i < num; i++){
            dp[i] = cuboids[i][2];
            for(int j = 0; j < i; j++){
                if(cuboids[j][0] <= cuboids[i][0] && cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2]){
                    dp[i] = Math.max(dp[i], dp[j] + cuboids[i][2]);
                }
            }
            // 关键！
            ans = Math.max(ans, dp[i]);
        }
        return ans;
    }
}

【leetcode hot 100】96. 不同的二叉搜索树

题目描述

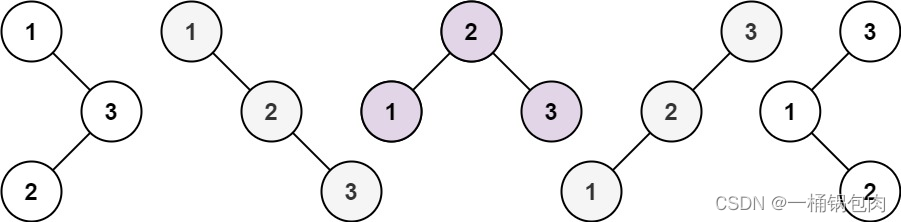
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

题目解析

【组合】：该题可以看作是左右子树的组合。比如对于节点个数为5时，左子树的节点个数为0，右子树的节点个数为4，此时的个数为右子树的组合数；假设左子树的节点个数为2，右子树的节点个数为2，此时的个数为右子树的组合数 * 左子树的组合数。

class Solution {
    public int numTrees(int n) {
        if(n == 1) return 1;
        // 相当于组合,也就是根结点的左右子树的组合
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i <= n; i++){
            // j代表左子树节点的个数
            for(int j = 0; j < i; j++){
                dp[i] += dp[j] * dp[i - j - 1];
            }
        }
        return dp[n];
    }
}