各位好,博主新建了个公众号《自学编程村》,拉到底部即可看到,有情趣可以关注看看哈哈,关注后还可以加博主wx呦~~~(公众号拉到底部就能看到呦)
我们刚刚在上一节讲述了TCP的滑动窗口。殊不知,它在我们OJ当中也是有应用的。
我们来介绍几道题目来看看:
1、寻找异位词
438. 找到字符串中所有字母异位词 - 力扣(Leetcode)
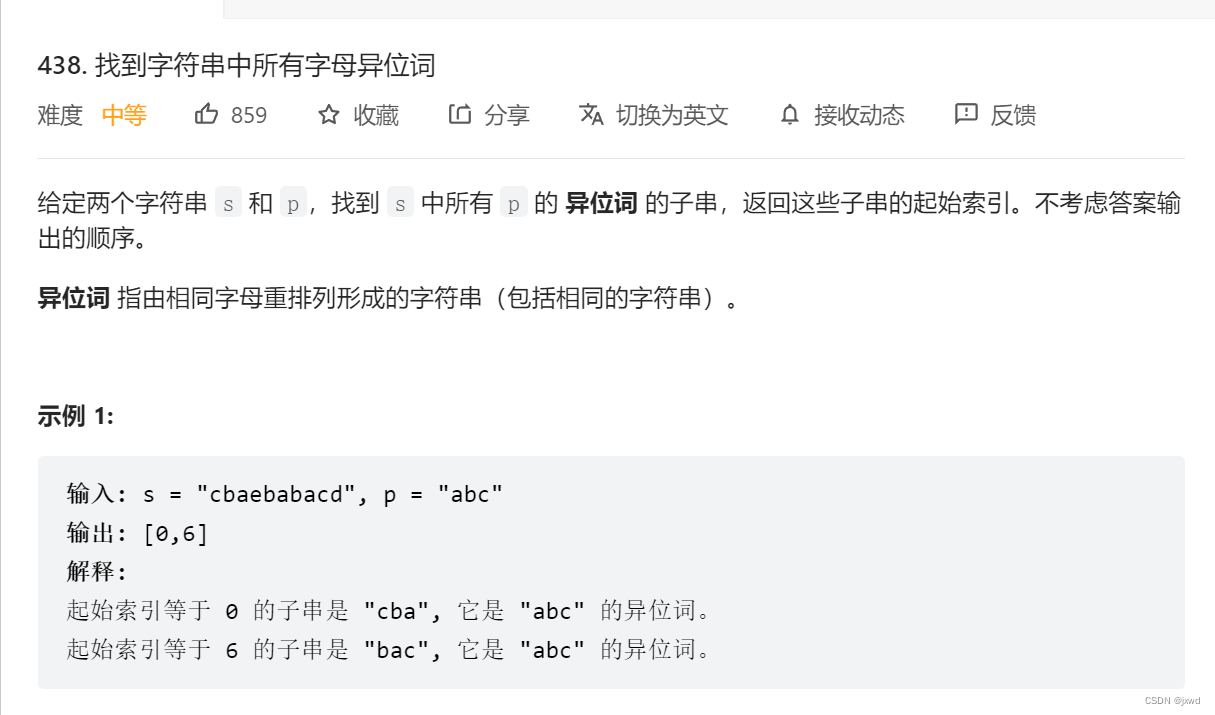
这道题就可以很好地利用滑动窗口来解决。
代码附下,在代码给出之前,需要指出一些需要注意的地方。
1、滑动窗口需要注意的是:充分利用其特性——在滑动的时候,中间的大部分元素都是不变的,变化的仅仅是滑动窗口的两端。
2、滑动窗口可以进行优化:不需要重新开辟数组用于维护判断的条件,可以用差值来进行计算。
3、注意一个元素在滑动窗口中统计的时候是加还是减。我们这里统一约定:一个元素只要在滑动窗口中,就加,否则,就减。像本题的其他条件(串p)是用来将滑动窗口中的数据抵消掉的(所以抵消掉和元素不在都是减)。 —— 我们的核心是围绕着数据是否在滑动窗口里。
代码如下:
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
int Ssize = s.size(),Psize = p.size();
if(Ssize < Psize){
return {};
}
int differ = 0;
vector<int> v;
vector<int> count(26,0);
for(int i = 0;i < Psize; i++){
--count[s[i]-'a'];
++count[p[i]-'a'];
}
for(auto& e: count){
if(e != 0){
++differ;
}
}
if(differ == 0){
v.push_back(0);
}
for(int i = 0;i < Ssize-Psize;i++){
if(count[s[i]-'a'] == -1){
--differ;
}
else if(count[s[i]-'a'] == 0){
++differ;
}
count[s[i]-'a']++;
if(count[s[i+Psize]-'a'] == 1){
--differ;
}
else if(count[s[i+Psize] - 'a'] == 0){
++differ;
}
count[s[i+Psize]-'a']--;
if(differ == 0){
v.push_back(i+1);
}
}
return v;
}
};我们再给出一道题:
2、滑动窗口最大值
239. 滑动窗口最大值 - 力扣(Leetcode)
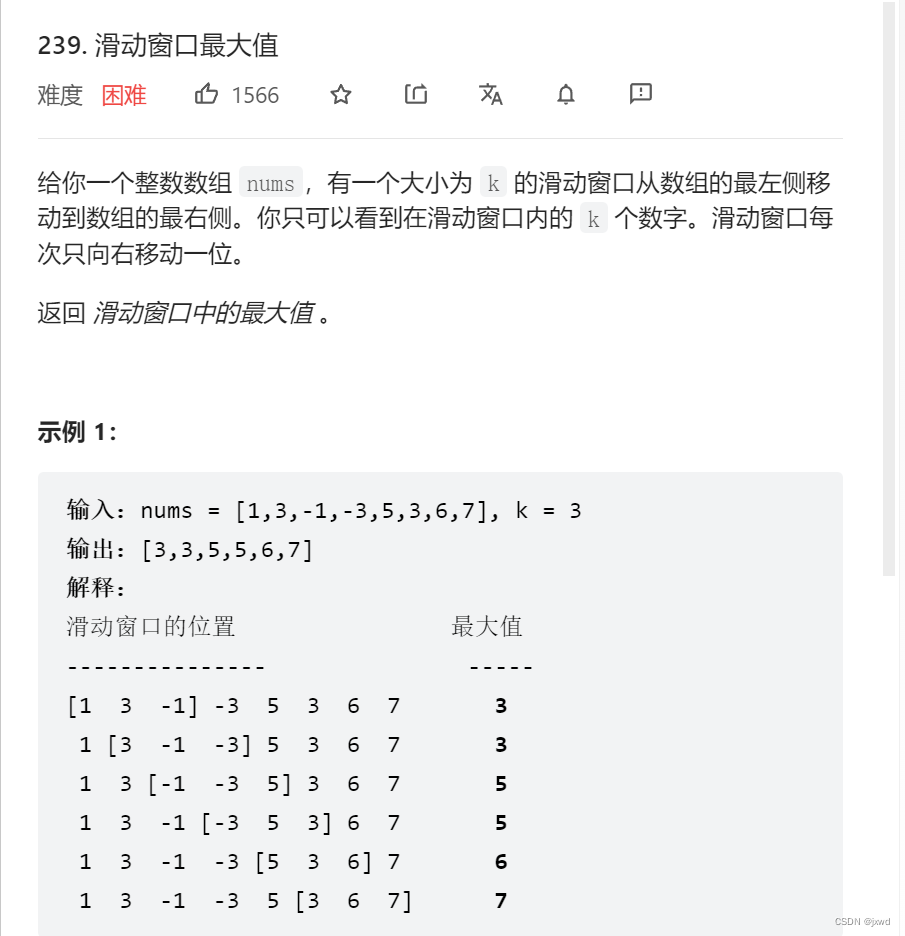
本题的难度实际一般,关键就是需要想到取最大的数的时候,不要着急去删除就可以了。
不论是用优先级队列,还是用双向队列,都用到了这一点思想:即如果是最大的值被删掉了而它却仍然在我们所创建的数据结构里,不需要慌,只要在出来的时候(top的时候)判断一下它是不是在我们滑动窗口的范围之内就可以了。
我们将运用优先级队列和双关队列的方法都给出:
//运用优先级队列求解
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> v;
priority_queue<pair<int,int>> mp;
if(nums.size() == 0)return {};
int max = nums[0];
for(int i = 0;i < k; i++){
mp.push(make_pair(nums[i],i));
if(max < nums[i]){
max = nums[i];
}
}
v.push_back(max);
for(int i = 0;i < nums.size() - k;i++){
mp.push(pair<int,int>(nums[i+k],i+k));
while(mp.top().second <= i){
mp.pop();
}
max = mp.top().first;
v.push_back(max);
}
return v;
}
};//运用双关队列求解
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
deque<int> dq;
vector<int> v;
for(int i = 0;i < k; i++){
while(!dq.empty() && nums[i] >= nums[dq.back()]){
dq.pop_back();
}
dq.push_back(i);
}
v.push_back(nums[dq.front()]);
//此时窗口已经形成
for(int i = k;i < nums.size();i++){
while(!dq.empty() && nums[i] >= nums[dq.back()]){
dq.pop_back();
}
dq.push_back(i);
while(dq.front() <= i - k){
dq.pop_front();
}
v.push_back(nums[dq.front()]);
}
return v;
}
};
好啦,本节的内容就到这里啦~~
原创不易,如果觉得写的不错,就点个赞呗~~~笔芯~~~~
下面是笔者的微信公众号,也欢迎来关注呀~~~



![[附源码]JAVA毕业设计校园失物招领管理系统(系统+LW)](https://img-blog.csdnimg.cn/263507da4c1f42d9929222d1dda90125.png)