每天一道C语言编程：Cylinder（圆柱体问题）

news2024/11/25 16:26:33

题目描述

使用一张纸和剪刀，您可以通过以下方式切出两个面形成一个圆柱体：
水平切割纸张（平行于较短的边）以获得两个矩形部分。
从第一部分开始，切出一个最大半径的圆。圆圈将形成圆柱体的底部。
将第二部分向上滚动，使其周长与圆的周长相等，并将滚动的一端连接到圆上。请注意，卷筒可能有一些重叠的部分，以获得所需的周长长度。

给定纸张的尺寸，您能否计算出可以使用上述程序构建的圆柱体的最大可能体积？

输入格式

输入由多个测试用例组成。每个测试用例由两个数字 w 和 h （1 ≤ w ≤ h ≤ 100）组成，它们表示纸张的宽度和高度。

最后一个测试用例后跟一行包含两个零。

输出格式

对于每个测试用例，打印一行具有最大可能体积的圆柱体。将此数字四舍五入到小数点后 3 位。

样例输入

样例输出

54.247
785.398
412.095

解题思路

根据题意可得对纸张的裁剪如下图所示

注：只是帮助理解，图不一定正确，第一部分裁剪圆，第二部分向上卷，将一端与圆拼接

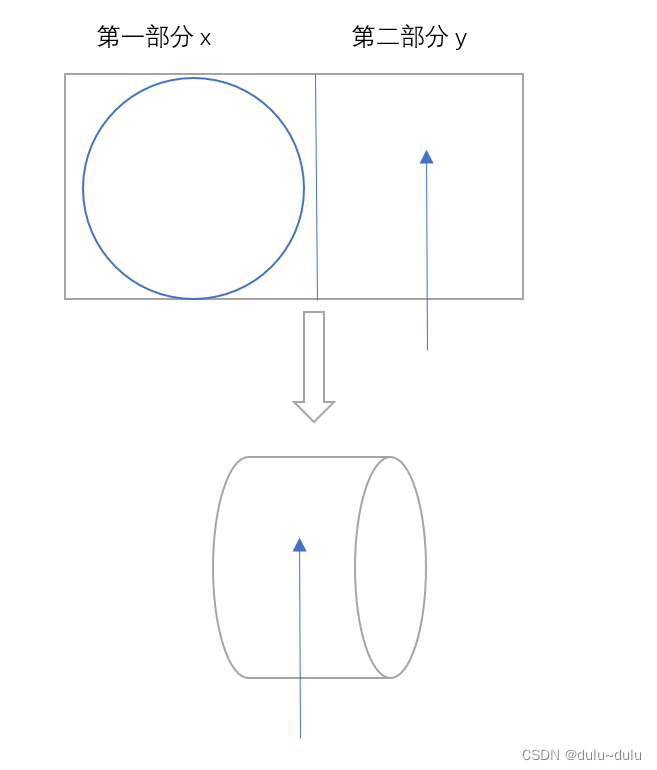
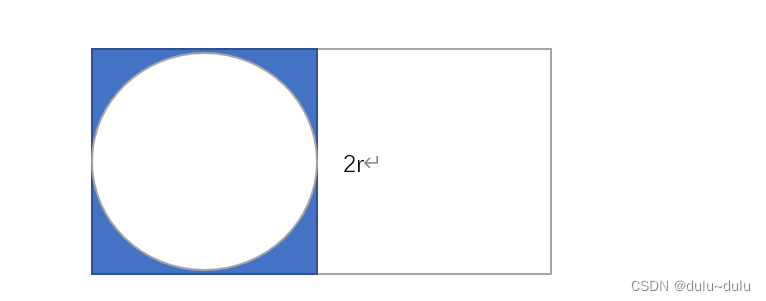
刚开始可能会像，第一部分划为正方形，利用率最高：

但是这样的话:2r>=2Πr,才能实现拼接，但是2r>=2Πr显然不成立，所以这样的想法是不正确的

不能投机取巧，只能从公式入手

V（圆柱体）= Π $r^{2}$ $\times h$ ，从公式可以看出，要使r与h尽量大，r受到宽度的影响，所以先考虑h，要使h尽量大，那么只有

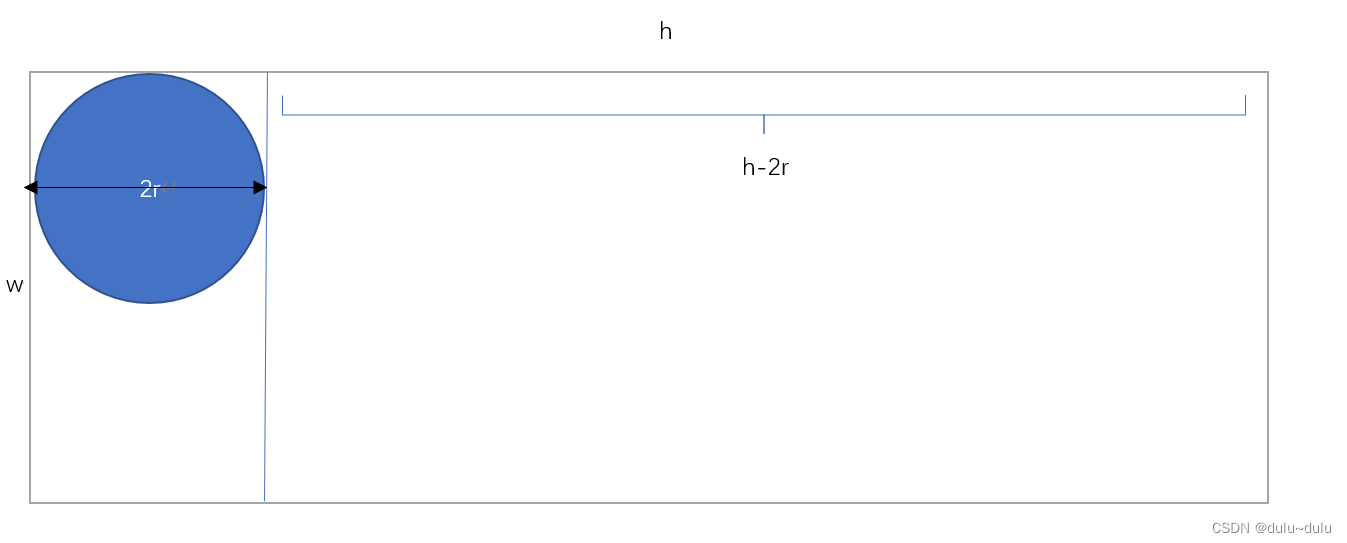
容易得到

$2\Pi r<=w$

$r<=w\div 2\Pi$

取最大： $r=w\div 2\Pi$

V(圆柱体)= $\Pi$ $\times$ $(w\div 2\Pi )^{2}$ $\times$ $(h-2(w\div 2\Pi ))$

以上是w作圆周长的情况，不能忽略h-2r作圆周长的情况，即

$2\Pi r$ $<=h-2r$

$r<=h\div (2\Pi +2)$

取最大： $r=h\div (2\Pi +2)$

V(圆柱体)= $\Pi \times (h\div (2\Pi +2))^{2}\times w$

到这里代码可写为

#include<stdio.h>
#include<math.h>

#define PI acos(-1)//定义PI为3.1415926535898
int main()
{
    double w,h;
    while(scanf("%lf %lf",&w,&h)&& w!=0 && h!=0)
    {
        double volumeone,volumetwo;
        double rone=w/(2*PI);
        volumeone=PI*pow(rone,2)*(h-2*rone);
        double rtwo=h/(2*PI+2);
        volumetwo=PI*pow(rtwo,2)*w;
        printf("%.3lf\n",volumeone>volumetwo?volumeone:volumetwo);
    }
    return 0;
}

但是可以看到运行结果是错误的，因为上述r都是由周长限制的，即

volumetwo： $2\Pi r$ $<=h-2r$ ;但是也要同时满足2r<=w,如果2r>w,那么r=w/2

可以这么理解，按照我们的图来讲

第一限制条件：2r<=w

第二限制条件： $2\Pi r$ $<=h-2r$

不满足第一限制条件，只考虑第二限制条件就会引起判断错误

而volomeone： $2\Pi r<=w$ ，本来就满足2r<=w，所以不需要写判断

所以volumetwo要加入判断

double rtwo=h/(2*PI+2)>w/2 ? w/2 : h/(2*PI+2);

最终代码为

#include<stdio.h>
#include<math.h>

#define PI acos(-1)//定义PI为3.1415926535898
int main()
{
    double w,h;
    while(scanf("%lf %lf",&w,&h)&& w!=0 && h!=0)
    {
        double volumeone,volumetwo;
        double rone=w/(2*PI);
        volumeone=PI*pow(rone,2)*(h-2*rone);
        double rtwo=h/(2*PI+2)>w/2 ? w/2 : h/(2*PI+2);
        volumetwo=PI*pow(rtwo,2)*w;
        printf("%.3lf\n",volumeone>volumetwo?volumeone:volumetwo);
    }
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/771637.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！