454. 四数相加 II

难度：medium

类型：哈希表

思路：

本题是使用哈希法的经典题目，而0015.三数之和 (opens new window)，0018.四数之和 (opens new window)并不合适使用哈希法，因为三数之和和四数之和这两道题目使用哈希法在不超时的情况下做到对结果去重是很困难的，很有多细节需要处理。

对于本题我们使用哈希法，先将nums1和nums2遍历相加后的结果放进map，key为数组对应的和，value为该和出现的次数。然后再对nums3和nums4进行遍历相加，去map中寻找其和的相反数，若找到，就累计其value存储的出现次数。

代码：

class Solution {
    public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        // key存放nums1和nums2中元素对应和，value存放和出现的次数
        Map<Integer, Integer> map = new HashMap<>();
        int len = nums1.length;
        // 遍历nums1和nums2的元素和
        for (int i: nums1) {
            for (int j: nums2) {
                int sum = i + j;
                map.put(sum, map.getOrDefault(sum, 0) + 1);
            }
        }
        // 统计满足条件的元组数量
        int ans = 0;
        // 遍历nums3和nums4的元素和
        for (int i: nums3) {
            for (int j: nums4) {
                int sum = i + j;
                if (map.containsKey(-sum)) {
                    ans += map.get(-sum);
                }
            }
        }

        return ans;
    }
}

复杂度分析：

时间复杂度： O(n^2)
空间复杂度: O(n^2)，最坏情况下A和B的值各不相同，相加产生的数字个数为 n^2

383. 赎金信

难度：easy

类型：哈希表

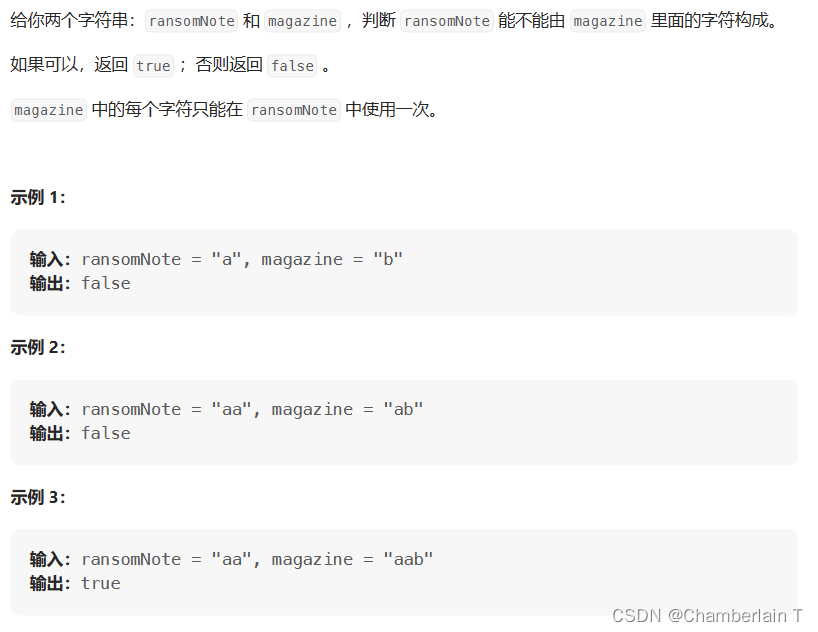
思路：

用数组做哈希表，类似于242.有效的字母异位词，但有略微的区别。用hash存储magazine每个字母出现的次数，再遍历ransomNote元素出现的次数，hash中若有元素小于0，则说明不行；

代码：

class Solution {
    public boolean canConstruct(String ransomNote, String magazine) {
        int[] hash = new int[26];

        for (int i = 0; i < magazine.length(); i++) {
            hash[magazine.charAt(i) - 'a']++;
        }
        for (int i = 0; i < ransomNote.length(); i++) {
            hash[ransomNote.charAt(i) - 'a']--;
        }
        for (int i: hash) {
            if (i < 0) {
                return false;
            }
        }
        return true;
    }
}

复杂度分析：

时间复杂度: O(n)
空间复杂度: O(1)

15. 三数之和

难度：medium

类型：哈希表，双指针

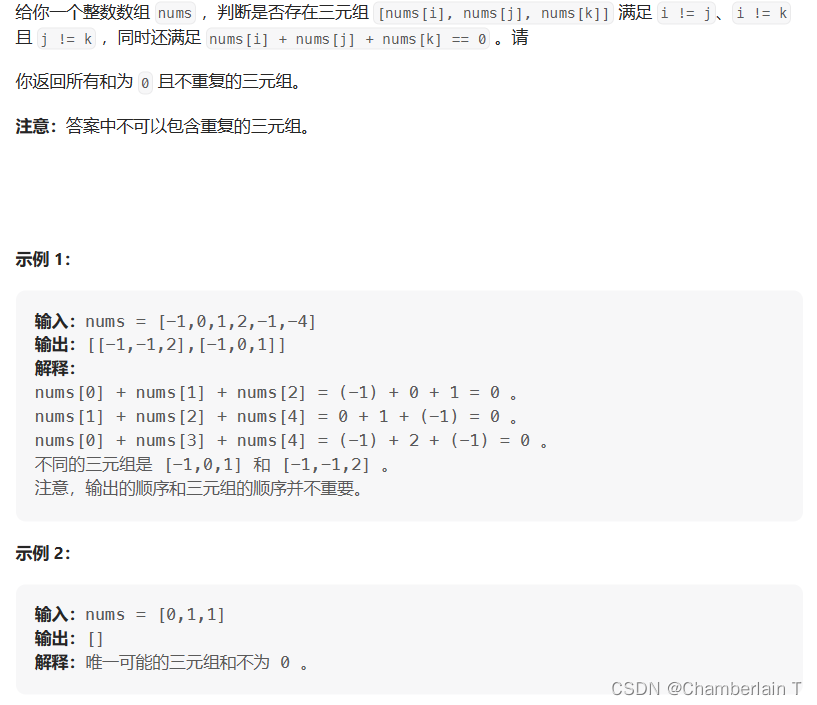
思路：

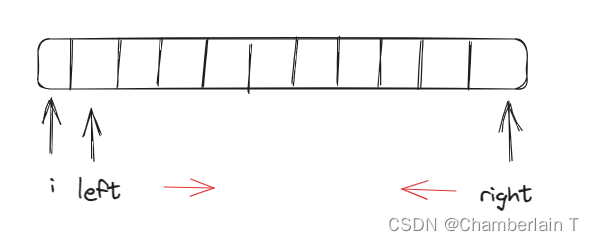
因为要去重，所以使用哈希法太复杂，我们使用双指针法；

i进行数组遍历，在每个i中，left和right分别从i+1和数组末尾相向出发；若nums[i] + nums[left] + nums[right] > 0 则right--，nums[i] + nums[left] + nums[right] < 0 则left++。

需要注意的去重：

对i去重，和后一个元素比较，为什么不是判断nums[i] == nums[i+1]呢？答：考虑[0,0,0]；
对right去重：若right > left && nums[right] == nums[right - 1]，则right--；
对left去重：同理

代码：

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        // 二维列表存储结果
        List<List<Integer>> ans = new ArrayList<>();
        // 数组排序
        Arrays.sort(nums);
        // i遍历数组，i为三元组的第一个数
        for (int i = 0; i < nums.length - 2; i++) {
            // 剪枝，如果最小的数大于0，那么三元组的和不可能为0
            if (nums[i] > 0) {
                break;
            }
            // 对i去重，和后一个元素比较，为什么不是判断nums[i] == nums[i+1]呢？
            // 答：考虑[0,0,0]特殊情况，
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            int left = i + 1;
            int right = nums.length - 1;
            // 开始移动left和right
            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right];
                // 符合条件，存入结果列表
                if (sum == 0) {
                    ans.add(Arrays.asList(nums[i], nums[left], nums[right]));
                    // 对right去重
                    while (right > left && nums[right] == nums[right - 1]) {
                        right--;
                    }
                    // 对left去重
                    while (right > left && nums[left] == nums[left + 1]) {
                        left++;
                    }
                    // 去重后，还需要再移动一次才是新的元素
                    right--;
                    left++;
                } else if (sum > 0) {
                    right--;
                } else if (sum < 0) {
                    left++;
                }
            }
        }
        return ans;
    }
}

复杂度分析：

时间复杂度: O(n^2)
空间复杂度: O(1)

18. 四数之和

难度：medium

类型：哈希表，双指针

思路：

卡哥的四数之和解析，写得很好

这道题是三数之和的扩展板，外面再套一层for就可以，五数之和、六数之和同理；

注意：

外面两层for都要进行去重;
剪枝，如果第一个数大于target了就没必要继续寻找四元组了（num[i]如果为负数的，负数相加会得到更小的负数，所以nums[i]>0;
防止溢出：long sum = (long)nums[i] + nums[j] + nums[left] + nums[right];

int的取值范围是-2,147,483,648 ~ 2,147,483,647，即-2^31 ~ 2^31-1。

long的取值范围是-9,223,372,036,854,775,808 ~ 9,223,372,036,854,775,807，即-2^63 ~ 2^63-1。

对于15.三数之和 (opens new window)双指针法就是将原本暴力O(n^3)的解法，降为O(n^2)的解法，四数之和的双指针解法就是将原本暴力O(n^4)的解法，降为O(n^3)的解法。

代码：

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> ans = new ArrayList<>();
        Arrays.sort(nums);

        for (int i = 0; i < nums.length - 3; i++) {
            // 剪枝，如果第一个数大于target了就没必要继续寻找四元组了（num[i]如果为负数的，负数相加会得到更小的负数，所以nums[i]>0）
            if (nums[i] > 0 && nums[i] > target) {
                break;
            }

            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }

            for (int j = i + 1; j < nums.length - 2; j++) {
                // i变成了三数之和
                if (j > i + 1 && nums[j] == nums[j - 1]) {
                    continue;
                }
                int left = j + 1;
                int right = nums.length - 1;
                
                while (left < right) {
                    // int sum = nums[i] + nums[j] + nums[left] + nums[right];
                    // 防止溢出
                    long sum = (long)nums[i] + nums[j] + nums[left] + nums[right];
                    if (sum == target) {
                        ans.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
                        while (left < right && nums[right] == nums[right - 1]) {
                            right--;
                        }
                        while (left < right && nums[left] == nums[left + 1]) {
                            left++;
                        }
                        right--;
                        left++;
                    } else if (sum > target) {
                        right--;
                    } else if (sum < target) {
                        left++;
                    }
                }
            }
        }
        return ans;
    }
}

复杂度分析：