学习资源选择

我从画面（一定要看清代码）
声音（清晰而不烦躁）
播放量（学的人多方便问）
名气（好象播放量跟这个有点成正比）
来比较一下
1 尚硅谷Java入门视频教程，宋红康java基础视频
必须要排在第一位。1600万的播放量呀。
717集我的天啦！
目录：
Java视频及配套资料下载指南
尚硅谷Java基础学习导读
001.尚硅谷_编程入门-资料文件结构1
002.尚硅谷_编程入门-资料文件结构2
003.尚硅谷_编程入门-入门概述
004.尚硅谷_编程入门-冯诺依曼体系结构
2 黑马
黑马程序员Java零基础视频教程_上部(Java入门，含斯坦福大学练习题+力扣算法题和大厂java面试题）
800多万的播放量
3 黑马
Java入门基础视频教程，java零基础自学就选黑马程序员Java入门教程（含Java项目和Java真题）
2 与3都是同样的200集，其实里面的目录也差不太多。
4 韩顺平零基础30天学会Java
910集。我的天啦！我的天啦！我的天啦！

最后选择

其实，JAVA并不是一门新语言，而大学里，培训机构里也多数以JAVA8做为主要的JDK版本，首先，我就以我的个人偏好来取舍了，我感觉超过300集的，看着头有点晕。所以，对不起韩老师了。而2套黑马的视频内容差不多，播放量也都不少，我细细的比较一下，发现 3 里的声音要稍好一些。
而2里的力扣与练习题你完全可以刷完了视频再直接看他的题不就好了？
力扣这个要大力推荐的
题库 - 力扣 (LeetCode) 全球极客挚爱的技术成长平台
再声明一下，JAVA技术相当的成熟，选择哪个真的是看个人的偏好，完全不存在哪个视频比哪个高级的问题。对于999还是1000的水平去教0或者1基础，其实是一样的。
也可以一部分的API，参见《黑马的JAVA学习路线–详解JAVA部分的学习》

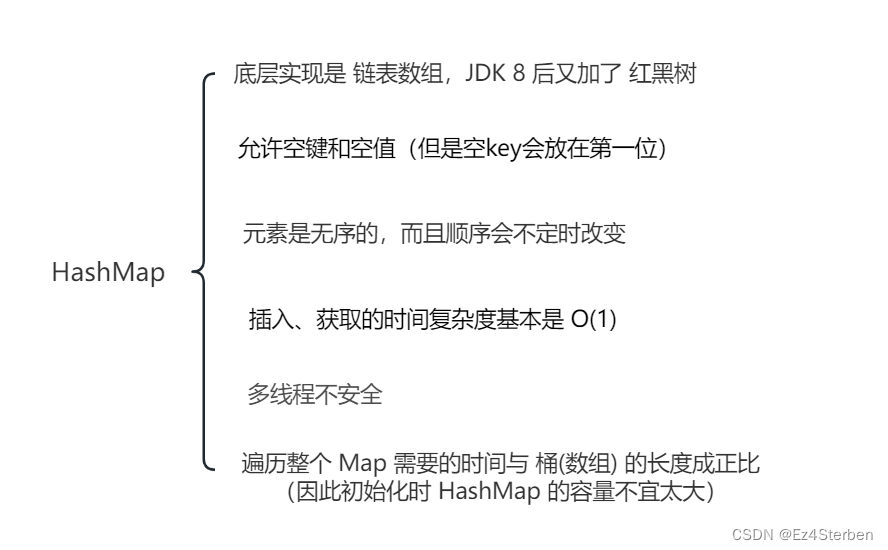
JAVA的知识范围

先来一张大的思维导图：
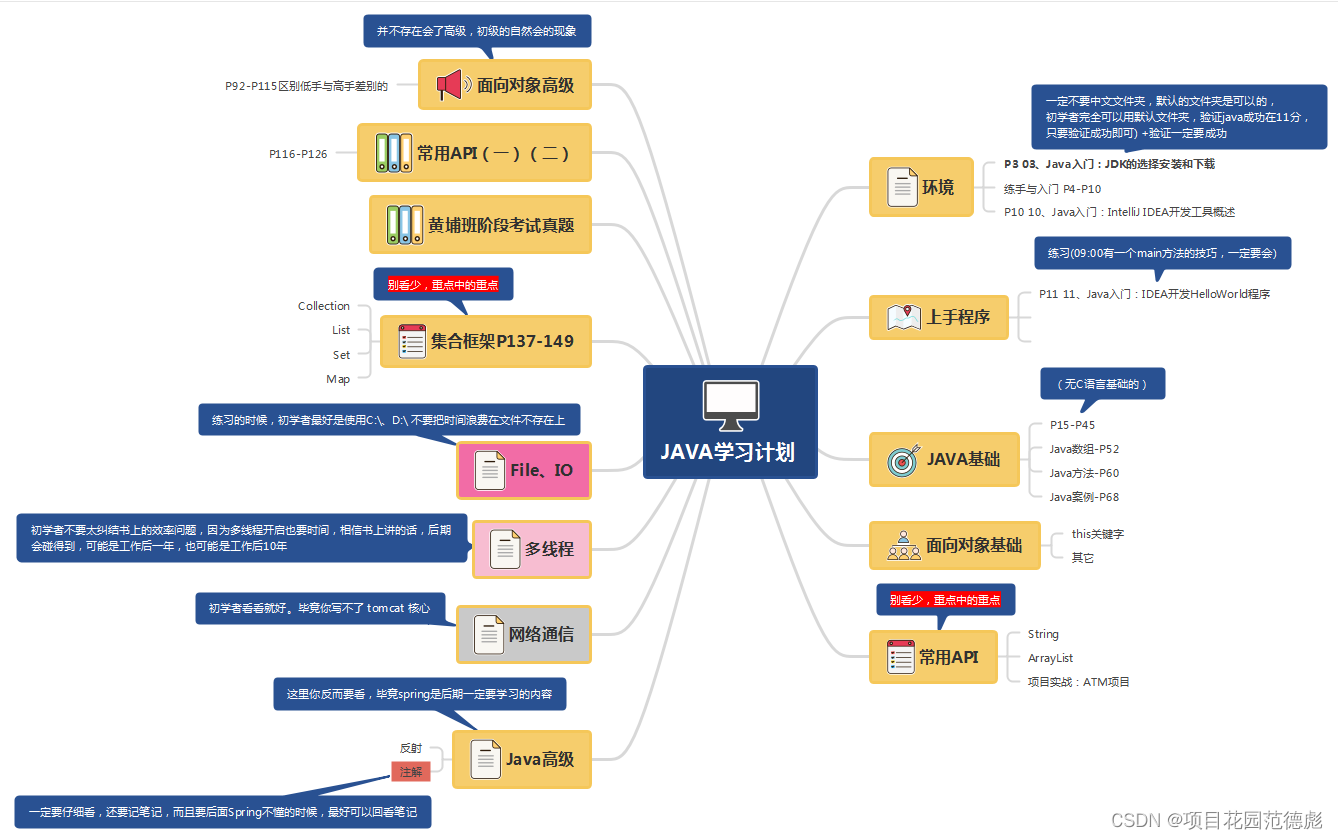
在这里插入图片描述
假定，我们的学习目标锁定在以后的spring上，或者蓝桥杯。

在这里插入图片描述
按着难度、相关性，先剔除一些技术。
第一个：网络编程（不是初学者能接触得到的，…）
第二个：多线程。（书上的例子都不会比单线程的快，上面的例子跟实战中使用相差太远）
第三个：文件IO（这个其实倒是不用剔除，但是初学者会不停的碰到IO异常，如果把文件名写死倒也算是正常的练习，但是问题是项目中上传，下载，都有现在的组件，而读写EXCEL的POI，好象也不太需要这一部分的基础）。

JDBC

黑马与尚硅谷的视频没有JDBC这部分内容，这个本来就没有准确划分，黑分的是在JAVAWEB的那套视频里讲了，尚硅谷的知识划分范围差不多。不过，韩老师的视频在这里有讲，这也是我为什么不选择韩老师视频的一个原因，就是它不是一套的。基本上，学习了JAVA的学生也不会不去学习JAVAWEB

swing与JAVAFX

可能有人会有一个疑问，我们大学里教材里有这个内容呀，学完黑马的这200多集还没有，其实尚硅谷的717集也同样没有swing的部分，甚至韩老师的900多集也同样没有，这个一个很在争议的部分，别写在这里了。

JAVA的学习步骤

还是先按着先易先难的这样的一个顺序。

1.右侧的部分:

不用多说了，这部分肯定都要学，但是，前面有几章是让你使用命令行来编译运行JAVA类的，这个其实可以跳过去，这个的最大作用其实是为了验证你的JDK安装是不是正确。
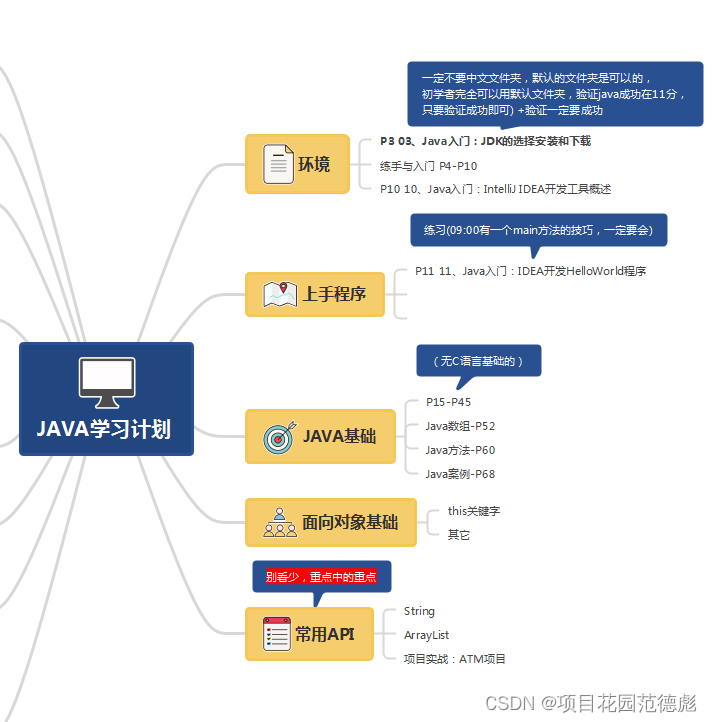
在这里插入图片描述

2 JAVA的高级但是必须要学的

有一些内容在JAVA的知识范畴是高级内容，但是你对于这些不但要学，而且还要精！
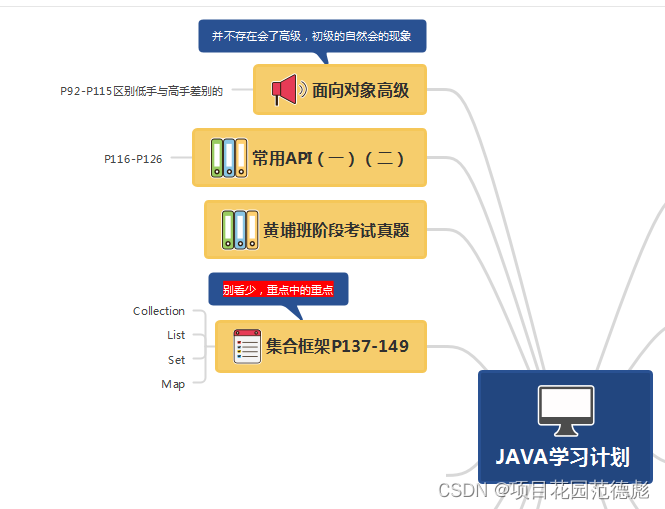
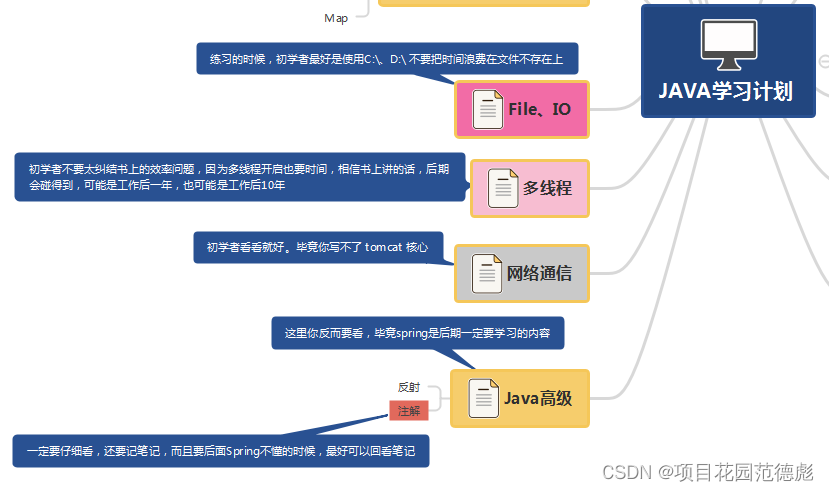
在这里插入图片描述

3 有一些要学（部分）

其实，很多的大学里的课程是比下面的还要多，也就是说，比蓝桥杯的知识内容还多。而反射，注解这个又不一定有。（毕竟这是JDK新版本的内容）
这里就不得不提一下教育部的本科培养计划，说白了就是本科就是为了培训硕士，进而培训博士。一定不能偏离科研。不管你本科毕业是不是想去企业里马上工作。就像操作系统教的不是使用操作系统，而是制作一个操作系统的知识，编译原理是自己做一个JAVB的自定义语言的编译器，等等。
所以，在一些比较卷的学校，很有可能会出现，项目能力最强的并不是绩点最高的。也不是JAVA成绩最高的。出现“忠孝两难全”的类似现象。
好在项目能力强的不是JAVA成绩最高，但是也肯定是相当的高的。
在这里插入图片描述

4力扣

其实呢，力扣只是一个有着大量的习题的网站，还有初，中，高级这样的划分。在最早的学习计算机的人群里，流行最多的就是《谭浩强C语言程序设计题解》–估计知道这本书的人年龄都不会小了。大家当时拿着这个东西如捧圣经。因为一门实践性的学科，练习才是重中之重。
在这里插入图片描述
现在学习的各种资源多了。所以大家学习的水平也自然就高了。

总结

提示：这里对文章进行总结：
JAVA的知识相当的繁杂，最忌讳的就是不停的看不停的看，想一口气把视频看完然后做项目。这种学习的方法在JAVA这里基本上就是欲速则不达。
不怕慢，就怕你不动手，就怕你每一周没有自己的代码！
动手多少，自己的代码写了多少，是你后面工资的积累。
JAVA还是比较遵循一万小时理论的，你花多少小时你以后就能拿多少工资的工作！