计算几何（二维），定理及证明（持续更新中..）

注：定理来自这篇博客，本文注重证明

向量基本运算

加法

向量 $\vec{a}=\left(x_1,y_1\right),\vec{b}=\left(x_2,y_2\right)$ 则 $\vec{a}+\vec{b}=(x_1+x_2,y_1+y_2)$
向量在加法中可以理解为一种移动效果，所以向量加法可以理解为下图：
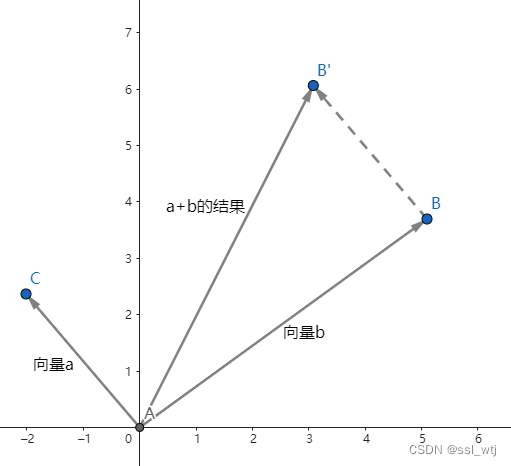
在这里插入图片描述

叉积

叉积的计算

向量 $\vec{a}=\left(x_1,y_1\right),\vec{b}=\left(x_2,y_2\right)$ 则 $\vec{a}\times \vec{b}=x_1y_2-x_2y_1$ ，证明如下：
首先，根据叉积的定义： $\vec{a}\times \vec{b}=\left|\vec{a}\right|\cdot|\vec{b}|\cdot \sin\left(\theta\right)$ （ $\left|\vec{a}\right|$ 表示 $\vec{a}$ 的模长，也就是长度， $\theta$ 表示从 $\vec{a}$ 旋转到 $\vec{b}$ 经过的角度，顺时针为正，逆时针为负）
定义 $a rc t an 2 (x, y)$ 表示从 $(1, 0)$ 顺时针旋转至 $(x, y)$ 经过的角度（返回弧度，取值为 $0\sim 2\pi$ ）
则原式可以表示为 $\sqrt{x_1^2+y_1^2}\cdot\sqrt{x_2^2+y_2^2}\cdot\sin\left(arctan2\left(x_2,y_2\right)-arctan2(x_1,y_1)\right)$
根据 $\sin(a-b)=\sin(a)\cos(b)-\cos(a)\sin(b)$ 可得： $原式=\sqrt{x_1^2+y_1^2}\cdot\sqrt{x_2^2+y_2^2}\cdot\left(\sin(arctan2(x_2,y_2))\cos(arctan2(x_1,y_1))-\cos(arctan2(x_2,y_2))\sin(arctan2(x_1,y_1))\right)$
由于每个表示为 $(x, y)$ 的向量放到平面直角坐标系上后实际上为：
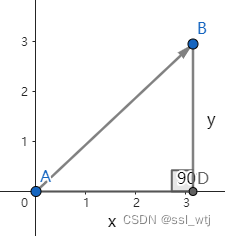
在这里插入图片描述
通过 $arctan2(x_2,y_2)$ 我们得到了 $\angle{BAD}$ 所以 $\sin(arctan2(x_2,y_2))=\sin(\angle{BAD})=\frac{BD}{AB}=\frac{y}{\sqrt{x^2+y^2}},\cos(arctan2(x_2,y_2))=\cos(\angle{BAD})=\frac{AD}{AB}=\frac{x}{\sqrt{x^2+y^2}}$
所以： $\begin{aligned}原式&=\sqrt{x_1^2+y_1^2}\cdot\sqrt{x_2^2+y_2^2}\cdot\left(\frac{y_2}{\sqrt{x_2^2+y_2^2}}\cdot\frac{x_1}{\sqrt{x_1^2+y_1^2}}-\frac{x_2}{\sqrt{x_2^2+y_2^2}}\cdot\frac{y_1}{\sqrt{x_1^2+y_1^2}}\right) \\ &=\sqrt{x_1^2+y_1^2}\cdot\sqrt{x_2^2+y_2^2}\cdot\frac{x_1y_2-x_2y_1}{\sqrt{x_1^2+y_1^2}\cdot\sqrt{x_2^2+y_2^2}} \\ &=x_1y_2-x_2y_1 \end{aligned}$

叉积的性质

画出 $\sin x$ 的曲线：
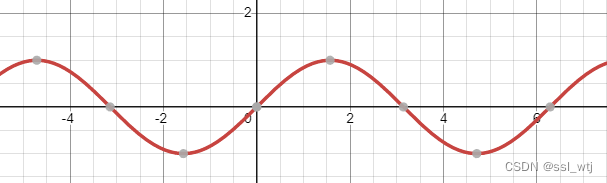
在这里插入图片描述
其正负性在 $x=\pi,2\pi,3\pi,....,n\pi$ 位置发生改变，这里的 $x$ 使用了弧度表示，相当于角度每增加或减少 $180\degree$ 发生一次改变。所以 $\vec{a}\times\vec{b}$ 的值当从 $\vec{a}$ 顺时针旋转至 $\vec{b}$ 经过的角度小于 $180\degree$ 时为正，否则为负（相当于朝向 $\vec{a}$ 方向时 $\vec{b}$ 若在左侧则为正，否则为负，这个性质可以用来判断左右转），并且若角度为 $0\degree$ 或 $180\degree$ 时为 $0$ （这个性质可以用来判断共线）。

点积

向量 $\vec{a}=\left(x_1,y_1\right),\vec{b}=\left(x_2,y_2\right)$ 则 $\vec{a}\cdot \vec{b}=x_1x_2+y_1y_2$ ，其证明方法与叉积大致相同，读者感兴趣的话可以自行证明，提示：

点积的定义： $\vec{a}\cdot \vec{b}=\left|\vec{a}\right|\cdot|\vec{b}|\cdot \cos\left(\theta\right)$
$\cos(a-b)=\sin(a)\sin(b)+\cos(a)\cos(b)$

另外，点积的性质为当 $-90<\theta<90$ 时值为负，当 $90<\theta<270$ 或 $-270<\theta<-90$ 时值为正（判断有无掉头），当 $x = 90, - 90, 270, - 270$ 时值为 $0$ （判断垂直）。证明方法也类似于叉积，提示：

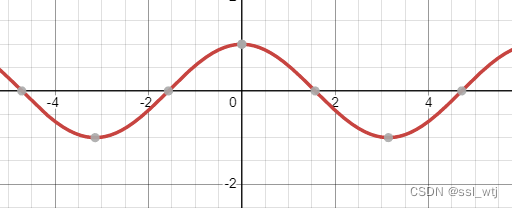
$\cos x$ 的曲线：

点与线

相交

判断线段是否相交

首先，感性理解一下，如果有两个线段相交，那么任意一条线段的两个端点一定在另一条线段的两侧，反之也成立（如下图）。

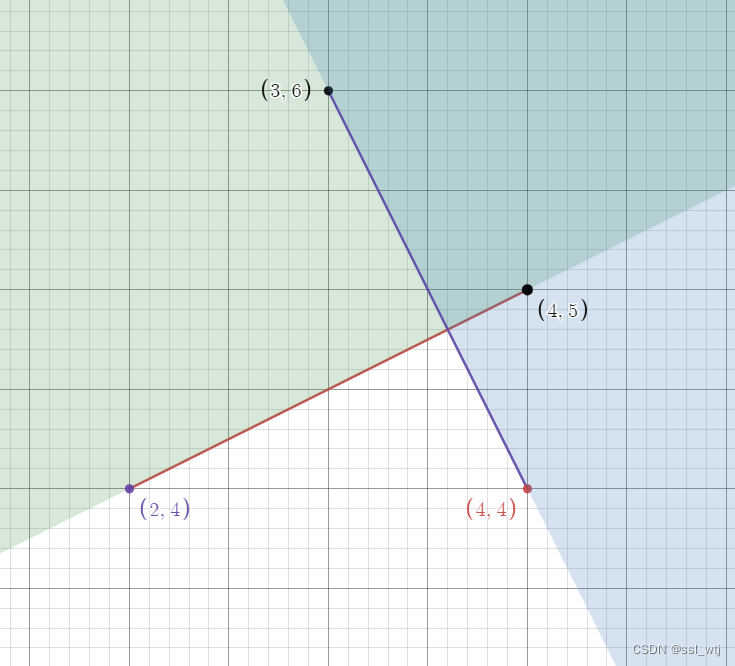
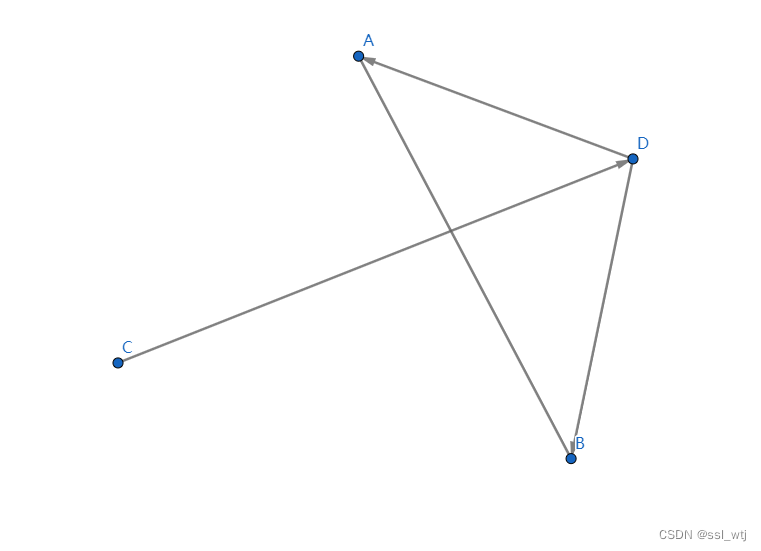
在这里插入图片描述
所以若将一条线段变成一个向量（一个端点指向另一端点），从终点向另外一条线段的两个端点走，必定一个向左拐，一个向右拐，所以叉积的正负性必定不同（如下图 $\vec{CD},\vec{DA},\vec{DB}$ ， $\vec{CD}\times\vec{DA}$ 和 $\vec{CD}\times\vec{DB}$ 的正负性不同）：
在这里插入图片描述
当然，也会出现特殊情况，就是两条线段重合：

此时，两线段相交，但叉积都为0（两向量方向相同或相反时叉积为0），但如果直接特判，依然会出问题，两线段共线：

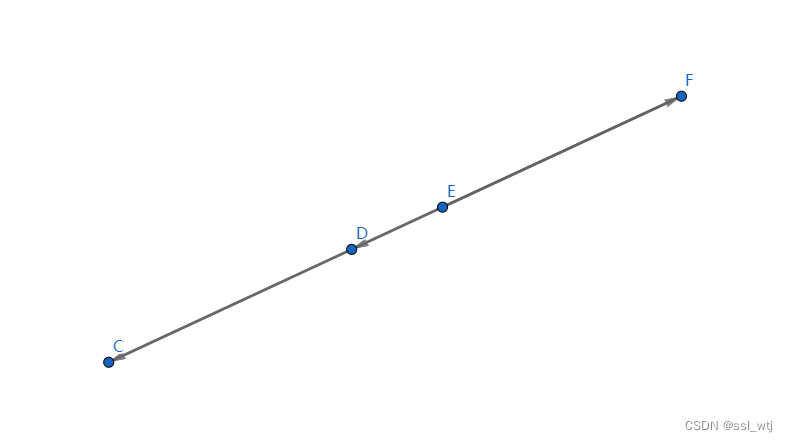
上图中线段CD与线段 EF共线，会出现错误的判断。所以，还需进一步完善判断条件——加入快速排斥实验。
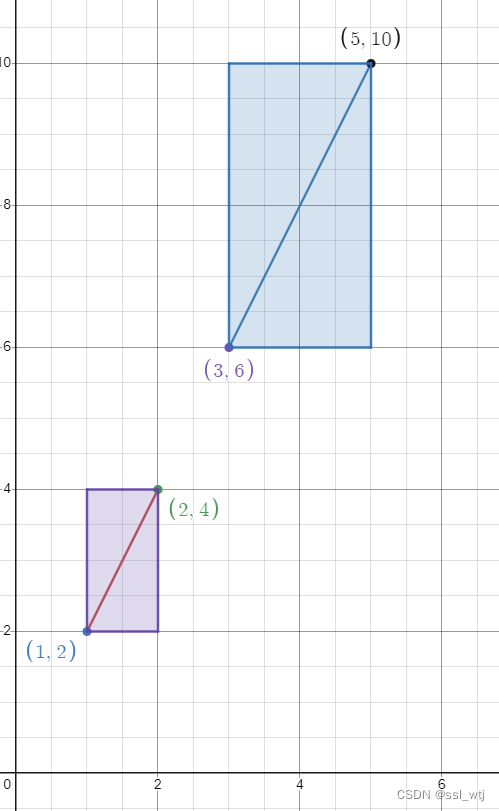
快速排斥实验，其目的是排除两线段共线但不相交的情况，即判断两个分别包含两线段的矩形是否有公共部分（如下图情况没有），只有出现了公共部分，两线段才可能相交。
在这里插入图片描述
这样下来，我们便解决了特殊情况，下面是代码：

#include<bits/stdc++.h>
namespace geometry
{
    using namespace std;
    struct Vector{//向量
        double x,y;
    };
    struct Point{//点
        double x,y;
    };
    struct Segment{//线段
        Point a,b;
    };
    struct Line{//直线
        Point a;
        Vector k;
    };
    double chk(double n)//判断n的正负性，n>0时返回1，n<0时返回-1，n=0时返回0
    {
        return (n>0?1:(n==0?0:-1));
    }
    double distance(Point a,Point b)//点之间的距离
    {
        return sqrt((b.x-a.x)*(b.x-a.x)+(b.y-a.y)*(b.y-a.y));
    }
    double operator *(Vector q,Vector h){//向量点乘
        return q.x*h.x+q.y*h.y;
    }
    Vector operator *(Vector q,double h){//向量扩大
        return (Vector){q.x*h,q.y*h};
    }
    Vector operator *(double q,Vector h){//向量扩大
        return (Vector){q*h.x,q*h.y};
    }
    Vector operator +(Vector q,Vector h){//向量加法
        return (Vector){q.x+h.x,q.y+h.y};
    }
    Point operator +(Point q,Vector h){//点加向量，实现位移
        return (Point){q.x+h.x,q.y+h.y};
    }
    Point operator -(Point q,Vector h){//点减向量，实现位移
        return (Point){q.x-h.x,q.y-h.y};
    }
    Vector operator -(Point q,Point h){//q-h，得到q->h的向量
        return (Vector){h.x-q.x,h.y-q.y};
    }
    double operator ^(Vector q,Vector h){//向量叉乘
        return q.x*h.y-q.y*h.x;
    }
    bool turn_left(Vector q,Vector h)//左转叉积大于0
    {
        return (q^h)>0;
    }
    bool turn_right(Vector q,Vector h)//右转叉积小于0
    {
        return (q^h)<0;
    }
    bool turn_back(Vector q,Vector h)//掉头点积小于0
    {
        return (q*h)<0;
    }
    bool vertical(Vector q,Vector h)//垂直点积等于0
    {
        return (q*h)==0;
    }
    bool segment_cross_check(Segment a,Segment b)//线段相交检测
    {
        if(min(a.a.x,a.b.x)>max(b.a.x,b.b.x)||min(a.a.y,a.b.y)>max(b.a.y,b.b.y)||min(b.a.x,b.b.x)>max(a.a.x,a.b.x)||min(b.a.y,b.b.y)>max(a.a.y,a.b.y))
            return false;//快速排斥实验
        double ans1=chk((a.a-a.b)^(b.a-a.a)),ans2=chk((a.a-a.b)^(b.b-a.a)),ans3=chk((b.a-b.b)^(a.a-b.a)),ans4=chk((b.a-b.b)^(a.b-b.a));
        return ans1!=ans2&&ans3!=ans4||ans1==0;//跨立实验
    }
}
using namespace std;
using namespace geometry;
int main()
{
    Segment a,b;
	cin>>a.a.x>>a.a.y>>a.b.x>>a.b.y>>b.a.x>>b.a.y>>b.b.x>>b.b.y;
	cout<<segment_cross_check(a,b);
	return 0;
}

直线相交

直线的表示

首先，介绍一下直线在计算几何中的常用表示方法：使用一个点和一个向量进行表示。
相信大家都学过一次函数，一次函数的格式为 $y=kx+b(k\ne 0)$ ，与一次函数的格式类似，这种方法的格式为 $b_x+xk_x,b_y+xk_y)$ （具体含义稍后解释）但 $k, b$ 与一次函数中完全不同。
对于两个点 $a, b$ 我们可以确定一条直线：
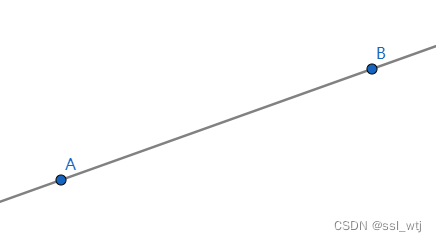
在这里插入图片描述
在 $y=kx+b(k\ne 0)$ 中， $k$ 是直线的斜率，也就是 $\frac{B_y-A_y}{B_x-A_x}$ 。而在 $b_x+xk_x,b_y+xk_y)$ 中， $k$ 是一个向量，从 $A$ 指向 $B$ 或从 $B$ 指向 $A$ ， $x$ 为一个实数，用来控制向量的长度和方向，表示 $x$ 和 $y$ 方向的位移。
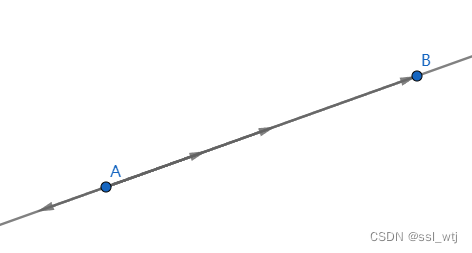
在这里插入图片描述
如此，我们便可以表示出该直线上的所有点。
为什么要这样表示一条线段？其实理由有很多，而其中我认为最重要的是：使用向量表示的直线，无需特殊考虑x方向差为0的情况（除0），当然，它也让许多计算更加简便。

求交点

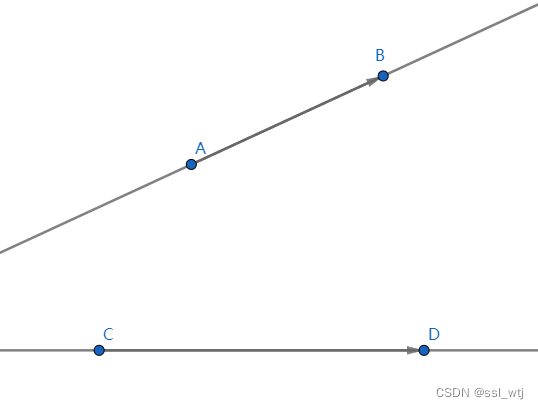
在这里插入图片描述
如何求出上图两条直线的交点？读者可以先自行思考，再往下翻。（本文只介绍几何做法，当然，也存在代数做法，感兴趣的话可以尝试自己寻找答案）

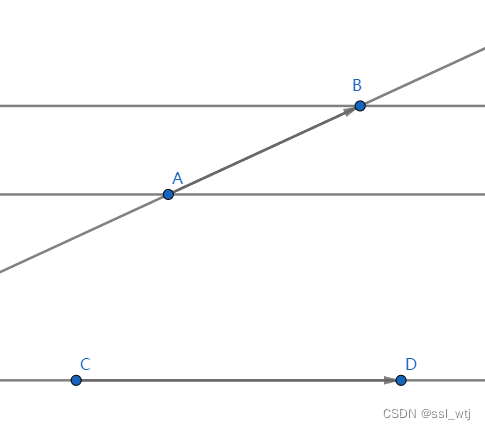
首先，过我们过 $A, B$ 两点做平行于 $C D$ 的直线：
在这里插入图片描述
容易发现，图中可以构造一对相似三角形（下图的 $\bigtriangleup ABH,\bigtriangleup IAG$ ），又因为 $\bigtriangleup ABH$ 的斜边实际上就是向量 $\vec{AB}$ ，如果我们可以得到两三角形任意一边的比例，就可以得到向量 $\vec{AI}$ 。那么如何得到边的比例呢？
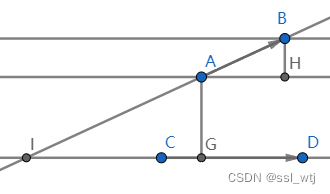
在这里插入图片描述
在过 $A$ 的平行线上截取一段长度等于 $\vec{CD}$ 模长的线段，分别向上和向下构造两个平行四边形。
$又\because S_上=|\vec{CD}|\cdot BH,S_下=|\vec{CD}|\cdot AG$
$\therefore S_上：S_下=BH:AG$
我们可以通过向量叉积求出两平行四边形的面积，之后便可得出比例求出交点。
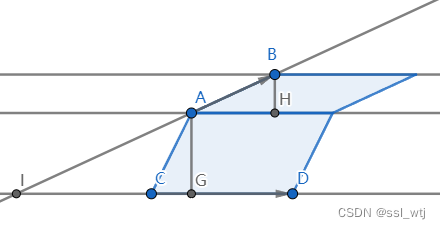
在这里插入图片描述
现在，考虑符号。我们发现，对于一条同直线，可以表示它向量有两个方向， $k$ 与 $- k$ 。下图是上图的另几个情况：

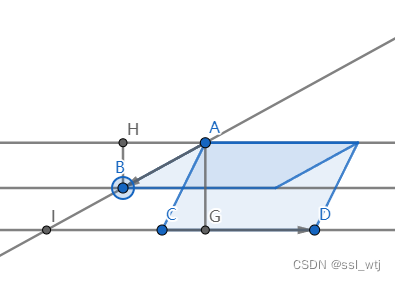
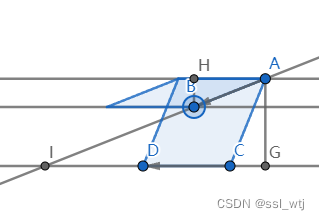
在这里插入图片描述

经过计算可以发现，不管是哪一种情况， $\vec{CD}\times\vec{CA}$ 与 $\vec{CD}\times\vec{AB}$ 如果符号相同，则 $I=A-\vec{AB}\cdot\frac{AG}{BH}$ 否则 $I=A+\vec{AB}\cdot\frac{AG}{BH}$ ，代码如下（前面已经给出的内容不再重复出现）：

bool line_cross_check(Line a,Line b)
{
    return (a.k^b.k)!=0;//在同一平面内两直线不平行才相交
}
bool point_on_line(Point a,Line b)
{
    return ((b.a-a)^b.k)==0;//三点共线
}
Point line_cross_get_cross_point(Line a,Line b)
{
    Vector c=b.a-a.a;
    return a.a-(b.k^c)/(b.k^a.k)*a.k;//得到带符号的比例
}

这个方法不仅可以求出直线交点，加上一些判断，它也可以求出线段交点。

距离

点到直线的距离

实际上这个问题十分简单，我们已经知道了叉积的几何意义是求出两向量所确定的平行四边形的带符号面积，那么可以构造出下图所示的平行四边形：
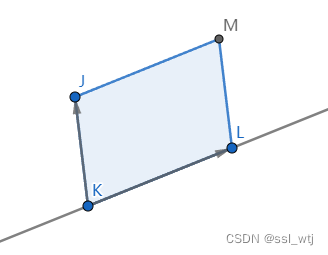
在这里插入图片描述
利用叉积求出它的面积，再除以 $|\vec{KL}|$ ，可以得出 $K L$ 边上的高，也就是 $J$ 到直线 $K L$ 的距离。
代码如下：

double distance_point_to_line(Point a,Line b)
{
    Vector c=b.a-a;
    return fabs((c^b.k)/distance(b.a,b.a+b.k));
}

点到线段的距离

与直线不同，线段是有长度限制的。所以一个点到一条线段的距离有两种情况：
在这里插入图片描述
首先，在线段两端点分别作两条垂直于该线段的直线，将平面分为绿色，红色和紫色三个部分。如果点出现在红色区域，距离相当于直接做垂线，计算方法同计算点到直线距离。
其实出现在绿色和紫色区域是等价的，其距离都是到线段两端点之一的距离（取最小值）。
那么如何判断出现再了哪一个区域？这时候，就要用到点积了！
在这里插入图片描述
根据点积的性质， $\vec{AB}\cdot\vec{BC}\ge0$ 说明从 $\vec{AB}$ 方向走到 $\vec{BC}$ 方向没有掉头，也就是点 $C$ 位于紫色区域，否则位于红色区域，判断是否位于绿色区域也是同理（但 $\vec{AB}$ 方向需要改成 $\vec{BA}$ 方向）。那么下面就是代码：

double distance_point_to_segment(Point a,Segment b)
{
    if(chk((b.a-b.b)*(b.b-a))==chk((b.b-b.a)*(b.a-a)))//判断是否在红色区域中
        return distance_point_to_line(a,(Line){b.a,(b.b-b.a)});//在红色区域中，返回垂线段长度
    else
        return min(distance(a,b.a),distance(a,b.b));//不在红色区域中，返回到线段两端点的最近距离
}

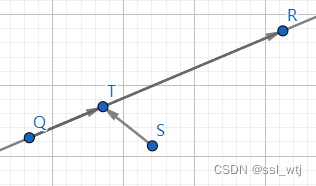
垂足

点在直线上的垂足

我们需要求出一个垂直于向量 $\vec{QR}$ 的向量 $\vec{ST}$ （ $T$ 为直线 $QR$ 上一点），根据点积的性质可以列出方程 $\vec{QR}\cdot\vec{ST}=0$ 。
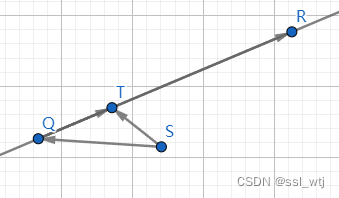
在这里插入图片描述
怎么解出一个向量？比较困难。我们可以尝试将 $\vec{ST}$ 换一种形式表示。
定义点 $a(x_1,y_1)$ 减去点 $b(x_2,y_2)$ 的结果为向量 $\vec{c}=(x_2-x_1,y_2-y_1)$ （从 $a$ 连接到 $b$ 的向量）。
所以 $\vec{ST}=\vec{(Q-S)}+\vec{QT}=\vec{(Q-S)}+x\cdot\vec{QR}$ （ $x$ 为一实数，在此处扩大或缩小向量 $\vec{QR}$ ）。
在这里插入图片描述
现在，需要使用点积的分配律继续下一步推导。先证明一下：
$\vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2),\vec{c}=(x_3,y_3)$
$\vec{a}\cdot\left(\vec{b}+\vec{c}\right)=\vec{a}\cdot\vec{(x_2+x_3,y_2+y_3)}=x_1(x_2+x_3)+y_1(y_2+y_3)$
$\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}=x_1x_2+y_1y_2+x_1x_3+y_1y_3=x_1(x_2+x_3)+y_1(y_2+y_3)$
$\therefore \vec{a}\cdot\left(\vec{b}+\vec{c}\right)=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}$
好的，现在实践运用一下：
$\begin{aligned} \vec{QR}\cdot\left(\vec{\left(Q-S\right)}+\left(x\cdot\vec{QR}\right)\right)&=0 \\\vec{QR}\cdot\vec{\left(Q-S\right)}+\vec{QR}\left(x\cdot\vec{QR}\right)&=0 \\\vec{QR}\cdot\vec{\left(Q-S\right)}+x\cdot\vec{QR}\cdot\vec{QR}&=0 \\x\cdot\vec{QR}\cdot\vec{QR}&=-\vec{QR}\cdot\vec{\left(Q-S\right)} \\x&=-\frac{\vec{QR}\cdot\vec{\left(Q-S\right)}}{\vec{QR}\cdot\vec{QR}} \end{aligned}$
现在，我们得出了向量 $\vec{QT}=x\cdot\vec{QR}$ ，定义点 $a (x, y)$ 加上向量 $\vec{b}=(x_1,y_1)$ 的结果为点 $c(x+x_1,y+y_1)$ ，所以 $T=Q+\vec{QT}=Q+x\cdot\vec{QR}$ ，代码如下：

Point foot_point(Point a,Line b)
{
    return b.a-b.k*(b.k*(a-b.a)/(b.k*b.k));//推导过程长，但结论简单
}

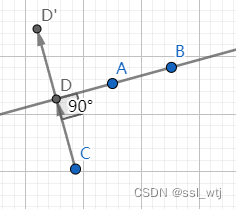
点对于一条直线的对称点

对于一条直线对称的两个点到这一条直线的距离相等。也就是说，当我们找到了这个点在直线上的垂足，再将它们相连得到向量，并且将其扩大一倍后加上原始点后，所得到的点就是所求得的对称点（见下图）。
在这里插入图片描述
代码：

Point symmetric_point(Point a,Line b)
{
    Point c=foot_point(a,b);//得到垂足
    return a+2*(a-c);//得到对称点
}