论文链接：Objects as Points

1. 解决了什么问题？

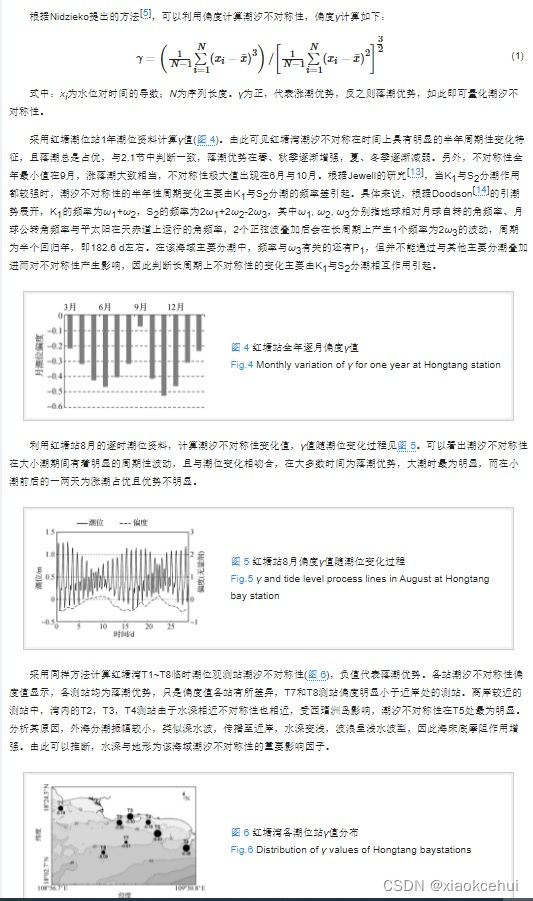
目标检测的任务是从图像中检出目标的矩形框。现有的检测方法大多会穷举所有潜在的目标位置，然后做分类。这非常浪费资源、低效率，并且依赖后处理。单阶段方法会在图像上放置大量的 anchors，然后直接分类。双阶段方法则会对候选边框的特征进行二次计算，做分类。然后这些方法计算 IoU，通过 NMS 后处理去除冗余的预测框。这类后处理操作是不可微的，训练起来比较困难，因此大多数的检测器的训练并不是端到端的。下图展示了 anchor-based 检测器和 CenterNet 在正负样本分配的差异。

2. 提出了什么方法？

本文将目标检测建模为关键点预测问题，通过关键点预测得到中心点位置，然后回归出所有的属性，如尺寸、3D 坐标、朝向角，甚至姿态。对于 3D 框预测，CenterNet 回归目标的绝对深度、3D 框的维度和朝向角。

2.1 Preliminaries

用$I\in {\mathbb{R}}^{W\times H\times 3}$表示输入图像，宽度为$W$，高度为$H$。目的是输出一张关键点热力图$\hat{Y}\in [0,1{]}^{\frac{W}{R}\times \frac{H}{R}\times C}$，其中$R$是输出步长，$C$是类别数。对于目标检测任务，$C=80$；本文中，默认步长$R=4$。输出步长以系数$R$对预测结果做下采样。${\hat{Y}}_{x,y,c}=1$表示一个检测到的关键点，而${\hat{Y}}_{x,y,c}=0$表示背景类。使用一个全卷积的 encoder-decoder 从输入图像$I$预测$\hat{Y}$：stacked hourglass 网络、ResNet 和 DLA。

对于类别$c$的 ground-truth 关键点$p\in {\mathbb{R}}^2$，计算得到它对应的低分辨率$\tilde{p}=\lfloor \frac{p}{R}\rfloor$。然后使用高斯核$Y_{xyc}=\exp (-\frac{(x-{\tilde{p}}_x{)}^2+(y-{\tilde{p}}_y{)}^2}{2{\sigma }_p^2})$，将所有的 ground-truth 关键点拍到一个热力图$Y\in [0,1{]}^{\frac{W}{R}\times \frac{H}{R}\times C}$上，${\sigma }_p$是一个对目标大小自适应的标准差。如果同类别的两个高斯区域有重叠，就逐像素地取二者的较大值。这部分的损失函数参考了 focal loss：

$$L_k=\frac{-1}{N}\sum _{xyc}\{\begin{array}{lc}(1-{\hat{Y}}_{xyc}{)}^{\alpha }\cdot \log ({\hat{Y}}_{xyc}),& \text{if}{Y}_{xyc}=1\\ (1-Y_{xyc}{)}^{\beta }\cdot ({\hat{Y}}_{xyc}{)}^{\alpha }\cdot \log (1-{\hat{Y}}_{xyc}),& \text{otherwise}\end{array}$$

本文默认$\alpha =2,\beta =4$是 focal loss 的超参数，$N$是图像$I$中关键点的个数。
为了弥补输出步长造成的离散误差，对于每个中心点，额外地学习一个局部偏移量$\hat{O}\in {\mathbb{R}}^{\frac{W}{R}\times \frac{H}{R}\times 2}$。对于所有的类别，该偏移量的学习是一样的。用 L1 损失训练该偏移量的学习：
$$L_{off}=\frac{1}{N}\sum _p\left|{\hat{O}}_{\tilde{p}}-(\frac{p}{R}-\tilde{p})\right|$$
该监督只作用于关键点$\tilde{p}$，其它位置忽略不计。

2.2 Objects as Points

用$(x_1^{(k)},y_1^{(k)},x_2^{(k)},y_2^{(k)})$表示目标$k$的边框，类别是$c_k$。它的中心点位于$p_k=(\frac{x_1^{(k)}+x_2^{(k)}}{2},\frac{y_1^{(k)}+y_2^{(k)}}{2})$。使用关键点预测器$\hat{Y}$来预测所有的中心点。然后对于每个目标$k$，回归目标的大小$s_k=(x_2^{(k)}-x_1^{(k)},y_2^{(k)}-y_1^{(k)})$。为了节省计算量，对所有的类别使用相同的尺寸预测器$\hat{S}\in {\mathbb{R}}^{\frac{W}{R}\times \frac{H}{R}\times 2}$。用 L1 损失来学习尺寸预测：
$$L_{size}=\frac{1}{N}\sum _{k=1}^N\left|{\hat{S}}_{p_k}-s_k\right|$$
不对尺寸做归一化操作，直接用原始的像素坐标值。整体的训练损失是：
$$L_{det}=L_k+{\lambda }_{size}{L}_{size}+{\lambda }_{off}{L}_{off}$$

在所有的实验中，${\lambda }_{size}=0.1$，${\lambda }_{off}=1$。作者使用单个网络来训练关键点预测$\hat{Y}$、偏移量$\hat{O}$和尺寸$\hat{S}$。网络在每个位置预测$C+4$个输出。所有的输出共享一个全卷积主干。对于每个任务模态，将主干特征分别输入一个由$3\times 3$卷积、ReLU 和$1\times 1$卷积组成的 head。下图展示了该网络的输出：

From points to bounding boxes

推理时，首先提取每个类别热力图的极大点。如果某个点的值大于等于其相邻的$8$个点的值，则保留作为极大点，我们一共保留$100$个极大点。用${\hat{\mathcal{P}}}_c$表示由$n$个检测到的中心点组成的集合，对于类别$c$， P ^ = { ( x ^ i , y ^ i ) } i = 1 n \hat{\mathcal{P}}=\left\{(\hat{x}_i,\hat{y}_i)\right\}_{i=1}^n P^={(x^i​,y^​i​)}i=1n​。每个关键点的坐标由整数坐标表示$(x_i,y_i)$。使用关键点的值${\hat{Y}}_{x_i{y}_{i}c}$表示检测的置信度，输出每个位置的边框：

$$({\hat{x}}_i+\delta {\hat{x}}_i-{\hat{w}}_i/2,{\hat{y}}_i+\delta {\hat{y}}_i-{\hat{h}}_i/2,{\hat{x}}_i+\delta {\hat{x}}_i+{\hat{w}}_i/2,{\hat{y}}_i+\delta {\hat{y}}_i+{\hat{h}}_i/2)$$

其中$(\delta {\hat{x}}_i,\delta {\hat{y}}_i)={\hat{O}}_{{\hat{x}}_i,{\hat{y}}_i}$是预测的偏移量，$({\hat{w}}_i,{\hat{h}}_i)={\hat{S}}_{{\hat{x}}_i,{\hat{y}}_i}$是预测的尺寸。所有的输出直接来自于关键点预测，无需 NMS 或其它后处理。提取极大点可以替代 NMS，在边缘设备上用$3\times 3$最大池化操作实现。

2.3 3D 检测

3D 检测预测每个目标的三维框，需要为每个中心点提供三个额外的属性：深度、3D 维度和朝向角。CenterNet 为每个属性都增加一个 head。在每个中心点，深度$d$是个标量，但是深度值很难直接回归得到。作者使用$d=1/\sigma (\hat{d})-1$计算深度，$\sigma$是 sigmoid 函数。将深度作为关键点预测器的一个额外通道$\hat{D}\in [0,1{]}^{\frac{W}{R}\times \frac{H}{R}}$计算。它用两个卷积层和 ReLU 实现，然后计算输出值 sigmoid 的倒数。使用 L1 损失训练深度预测器。

目标的 3D 维度是$3$个标量。我们通过一个单独的 head $\hat{\Gamma }\in {\mathbb{R}}^{\frac{W}{R}\times \frac{H}{R}\times 3}$直接回归它们的绝对值，单位为米。使用 L1 损失训练。

朝向角也默认为一个单独的标量。但它很难直接回归。于是将朝向角表示为两个 bins，在每个 bin 内再回归具体的值。朝向角编码为$8$个标量，每个 bin 用$4$个标量表示。对于每个 bin，前两个标量用于 softmax 分类，后两个标量回归 bin 里面的角度。
网络输出深度特征图$\hat{D}\in {\mathbb{R}}^{\frac{W}{R}\times \frac{H}{R}}$、3D 维度$\hat{\Gamma }\in {\mathbb{R}}^{\frac{W}{R}\times \frac{H}{R}\times 3}$和朝向角编码$\hat{A}\in {\mathbb{R}}^{\frac{W}{R}\times \frac{H}{R}\times 8}$。对于每个目标实例$k$，从这三个特征图中提取 ground-truth 中心点附近的值，${\hat{d}}_k\in \mathbb{R},{\hat{\gamma }}_k\in {\mathbb{R}}^3,{\hat{\alpha }}_k\in {\mathbb{R}}^8$。将输出转换为绝对深度值后，用 L1 损失训练：

$$L_{depth}=\frac{1}{N}\sum _{k=1}^N\left|\frac{1}{\sigma (\widehat{d_k})}-1-d_k\right|$$
其中$d_k$是目标的绝对深度，单位是米。类似地，3D 维度也是用 L1 损失监督：
$$L_{dim}=\frac{1}{N}\sum _{k=1}^N\left|{\hat{\gamma }}_k-{\gamma }_k\right|$$

${\gamma }_k$是目标的高度、宽度和长度，单位是米。

朝向角$\theta$是个标量。作者将$8$个标量分为$2$个组，每个组代表一个角度 bin。一个 bin 的角度范围是$B_1=[-\frac{7\pi }{6},\frac{\pi }{6}]$，另一个是$B_2=[-\frac{\pi }{6},\frac{7\pi }{6}]$。因此，每个 bin 就有$4$个标量。在每个 bin 内，$2$个标量$b_i\in {\mathbb{R}}^2$用于 softmax 分类（如果朝向角落入 bin $i$）。其余的$2$个标量$a_i\in {\mathbb{R}}^2$分别是 bin 内偏移量（到 bin 中心$m_i$）的$\sin$值和$\cos$值。$\hat{\alpha }=[{\hat{b}}_1,{\hat{a}}_1,{\hat{b}}_2,{\hat{a}}_2]$。用 softmax 训练分类，用 L1 损失训练角度值：

$$L_{ori}=\frac{1}{N}\sum _{k=1}^N\sum _{i=1}^2(\text{softmax}({\hat{b}}_i,c_i)+c_i\left|{\hat{a}}_i-a_i\right|)$$

其中$c_i=\mathbb{I}(\theta \in B_i),a_i=[\sin (\theta -m_i),\cos (\theta -m_i)]$，$\mathbb{I}$是指标函数。用$8$个标量来解码出预测朝向角$\theta$，

$$\hat{\theta }=\arctan 2({\hat{a}}_{j1},{\hat{a}}_{j2})+m_j$$

其中$j$是分类得分较高的 bin 的索引。

实验设定

作者在 KITTI 数据集上做 3D 框预测的实验。KITTI 包含$7841$个训练图像，评价指标是$IoU=0.5$的$A{P}_{11}$。作者评价了 2D 框的 AP、朝向角 AOP 和 BEV AP。在训练和测试时的图像分辨率都是$1280\times 384$。一共训练用了$70$个 epochs，学习率在第$45$和$60$个 epoch 时做衰减。主干网络为 DLA-34，深度、朝向角和维度损失的权重都是$1$。

2.4 实现细节

使用了$4$种网络结构：ResNet-18、ResNet-101、DLA-34、Hourglass-104。作者用可变形卷积对 ResNet 和 DLA-34 做了修改。

Hourglass 使用 stacked Hourglass 网络对输入做$4\times$降采样，后面是$2$个连续的 hourglass 模块。每个 hourglass 模块都包括对称的$5$层 down-conv 和 up-conv 网络。这个网络很大，但能输出最佳的关键点预测。

ResNet 用$3$个 up-conv 网络改进了标准的 ResNet，得到更高分辨率的输出（输出步长为$4$）。首先将三个上采样层的通道改为$256,128,64$，以节省计算量。然后在每个 up-conv 前增加一个$3\times 3$可变形卷积。Up-conv 核用双线性插值初始化。
DLA 是一个带跳层连接的图像分类网络。针对密集预测任务，它使用 DLA 的全卷积上采样版本，通过迭代的深度聚合操作增加特征图分辨率。用可变形卷积增强跳层连接。在每个上采样层中，用$3\times 3$可变形卷积替换原始卷积。

在每个输出 head，增加一个$256$通道的$3\times 3$卷积层。最后用$1\times 1$卷积输出最终结果。