选择排序

思路图解

代码（C语言）

void Selection_Sort(ElementType A[], int N)
{
    for(i = 0; i < N; i++)
    {
        MinPosition = ScanForMin(A,i,N-1);
        //从A[i]到A[N-1]中找最小元，并将其位置赋给MinPosition
        Swap( A[i], A[MinPosition] );
        //将未排序部分的最小元换到有序部分的最后位置
    }
}

时间复杂度

$T=\Theta (N^2)$

要提高时间效率，关键在于如何快速找到最小元，所以引入堆排序：

堆排序

算法1

先看第一种算法：

void Heap_Sort(ElementType A[], int N)
{
    BuildHeap( A );    /*  o(N)  */
    for( i = 0; i < N; i++)
        TmpA[ i ] = DeleteMin( A );    /*  O(logN)  */
    for( i = 0; i < N; i++)      /*   O(N)   */
        A[ i ] = TmpA[ i ];  
}

它的思路是：

先将序列A建成堆，然后重复地从堆中提取最小元素，并将其存储在临时数组中，实现了堆排序算法。最后，它将排序后的元素复制回原始数组A。

时间复杂度： $T(N)=O(N{log_{}}^{}N)$

空间上，需要额外O（N）的内存占用，并且复制元素需要时间。

（在内存足够的情况下，一般没有问题；但如果在固定内存中使用这种算法的堆排序，就会出现无法完成排序的情况；例如：2GB满内存的情况下，要对该序列进行排序，那么实际就需要4GB的内存来进行堆排序。）

所以这种算法是不太好的。

算法2

void Heap_Sort(ElementType A[], int N)
{
    for(i = N/2 - 1; i >= 0; i--)
        PercDown(A ,i ,N);
    for(i = N - 1; i > 0; i--)
    {
        Swap(&A[0], &A[i] );
        PercDown(A ,0 ,i);
    }
}

算法2的思路是：

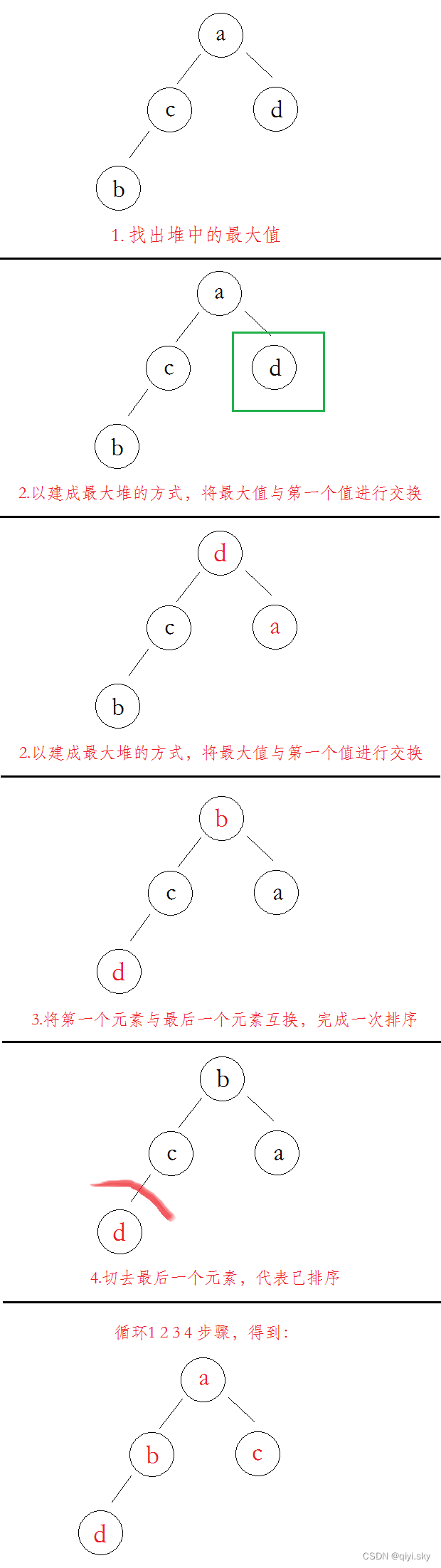
定理：

堆排序处理N个不同元素的随机排序的平均比较次数是 $2NlogN-O(Nlog\, logN)$

虽然堆排序给出最佳平均时间复杂度，但实际效果不如用Sedgewick增量序列的希尔排序。

堆排序代码

void Swap( ElementType *a, ElementType *b )
{
     ElementType t = *a; *a = *b; *b = t;
}
 
void PercDown( ElementType A[], int p, int N )
{ 
  /* 将N个元素的数组中以A[p]为根的子堆调整为最大堆 */
    int Parent, Child;
    ElementType X;

    X = A[p]; /* 取出根结点存放的值 */
    for( Parent=p; (Parent*2+1)<N; Parent=Child ) {
        Child = Parent * 2 + 1;
        if( (Child!=N-1) && (A[Child]<A[Child+1]) )
            Child++;  /* Child指向左右子结点的较大者 */
        if( X >= A[Child] ) break; /* 找到了合适位置 */
        else  /* 下滤X */
            A[Parent] = A[Child];
    }
    A[Parent] = X;
}

void HeapSort( ElementType A[], int N ) 
{ /* 堆排序 */
     int i;
      
     for ( i=N/2-1; i>=0; i-- )/* 建立最大堆 */
         PercDown( A, i, N );
     
     for ( i=N-1; i>0; i-- ) {
         /* 删除最大堆顶 */
         Swap( &A[0], &A[i] ); 
         PercDown( A, 0, i );
     }
}

end

学习自：MOOC数据结构——陈越、何钦铭

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/765076.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！