💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
在网格化数据集上执行2D高通、低通、带通或带阻滤波器是数字图像处理中常见的操作,可以通过以下步骤轻松实现:
1. 确定滤波器类型:首先确定所需的滤波器类型,如高通、低通、带通或带阻。高通滤波器可以提取图像中的细节和边缘信息,低通滤波器可以模糊图像并去除噪声,而带通和带阻滤波器则选择性地保留或去除一定频率范围内的信息。
2. 设计滤波器:根据所需的滤波器类型,设计相应的滤波器模板或频率响应。例如,常用的低通滤波器有均值滤波器、高斯滤波器等,而高通滤波器有拉普拉斯滤波器、Sobel滤波器等。带通和带阻滤波器可以通过设计频率响应来实现。
3. 进行滤波操作:将设计好的滤波器应用到网格化的数据集上。对于每个像素或网格点,使用滤波器模板对其周围的像素进行加权平均或其他运算。这可以通过卷积操作来实现,其中滤波器与图像进行卷积运算,得到滤波后的图像。
4. 处理边界效应:卷积操作通常会导致边界处的结果产生不准确的偏差。为了处理边界效应,可以使用边界填充方法,如零填充、对称填充或周期填充。这些方法可以在滤波之前对输入数据进行扩展,以确保边界处的滤波结果更加准确。
需要注意的是,在实际应用中,滤波器的选择和设计往往需要结合具体的问题和要求。此外,还可以使用现有的图像处理库或软件来进行滤波操作,如OpenCV、Scikit-image等,这些库提供了丰富的滤波函数和工具集。
总结起来,在网格化数据集上执行2D滤波器可通过确定滤波器类型、设计滤波器、进行滤波操作和处理边界效应来实现。
本文对格网数据集执行二维高斯加权移动窗口平均滤波器。它旨在简化将分辨率转换为像素的过程,并找出要使用的西格玛值。
📚2 运行结果
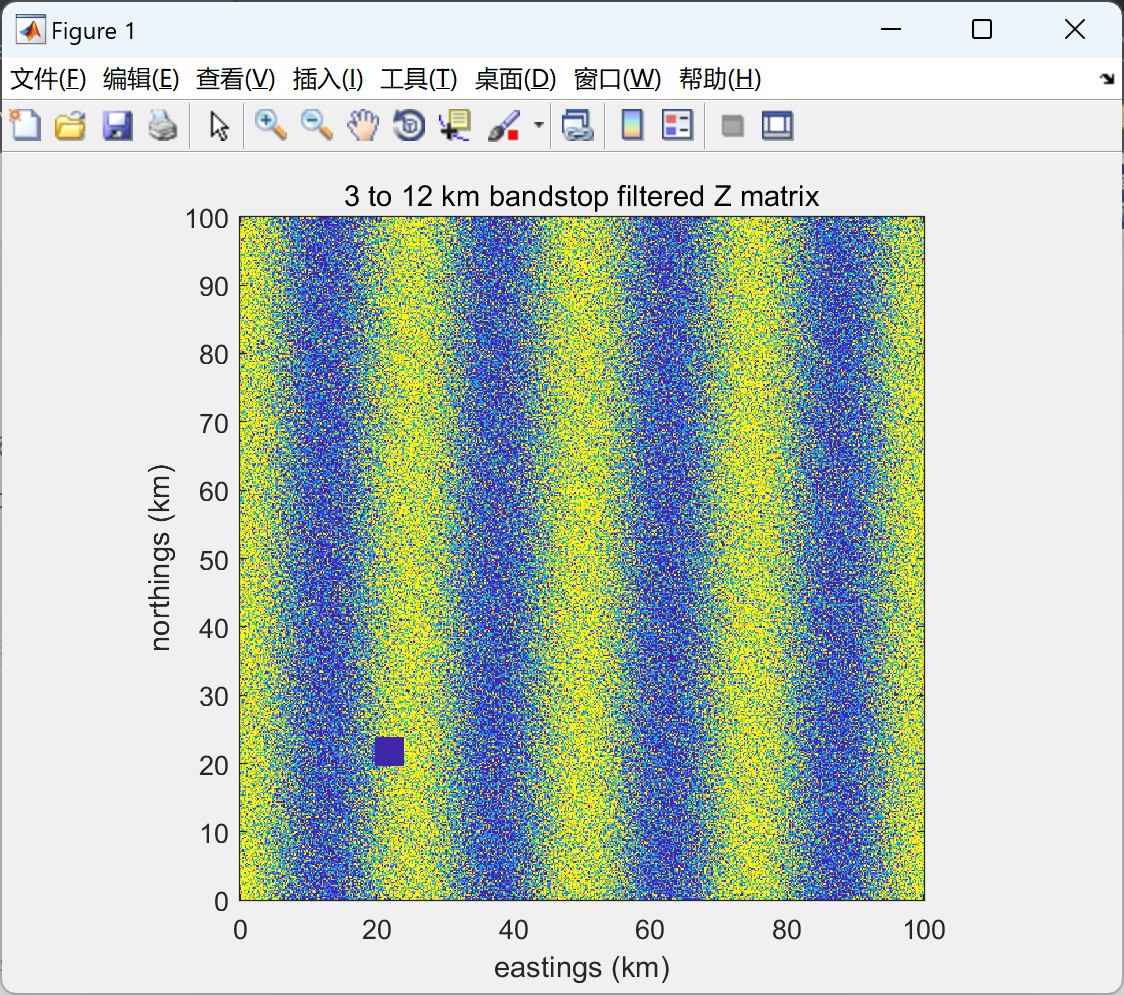
部分代码:
%
%% Syntax
%
% Zf = filt2(Z,res,lambda,filtertype)
%
%% Description
%
% |Zf = filt2(Z,res,lambda,filtertype)| filters 2D dataset |Z| that has resolution |res|,
% to an approximate wavelength |lambda|. If the |filtertype| is |'lp'| or |'hp'| for lowpass
% or highpass, |lambda| must be a scalar value. If the |filtertype| is |'bp'| or |'bs'| for
% bandpass or bandstop, |lambda| must be a two-element array of the two cutoff wavelengths.
%
%% Explanation of this type of filter
% There are many ways to filter a cat. The approach implemented by |filt2| is less complex than a 2D
% FFT, but slightly more nuanced than a simple 2D moving average.
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]赵瑾,吴笑峰.基于CFOA的低通、带通和高通滤波器[J].现代电子技术,2004(13):89-90+93.
[2]陈俊驰. 微带带阻滤波器的研究与设计[D].电子科技大学,2016.