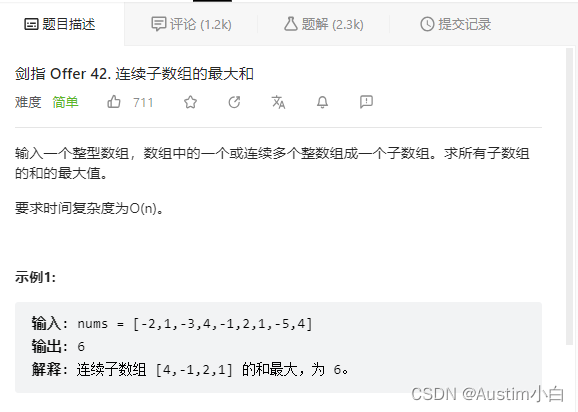
题目描述

方法一：超出时间限制
思路：选一个起点，选一个终点，计算起点到终点的和；求max；
起点几种可能：0 到 size -1;
终点： 起点 到 size -1；

int maxSubArray(int* nums, int numsSize){
    int maxSum, tempSum, i, j, k;
    maxSum = -101;
    for(i = 0;  i < numsSize; i++){
        for(j = i; j < numsSize; j++){
            tempSum = 0;
            for(k = i; k <= j; k++){
                tempSum += nums[k];
            } 
            if(tempSum > maxSum)
                maxSum = tempSum;
        }
    }
    return maxSum;
}

方法二：贪心算法
依次遍历数组的每个元素，并记录前面i - 1个元素的最大和preSum，若preSum < 0, 则从当前元素重新开始计算；若 preSum > 0，则当前最大和为preSum + nums[i]。

int maxSubArray(int* nums, int numsSize){
    if((nums == NULL) || (numsSize == 0))
        return 0;

    int maxRes = nums[0];
    int preSum = nums[0];

    for (int i = 1; i < numsSize; i++)
    {
        if (preSum < 0) {
            preSum = nums[i];
        } else {
            preSum += nums[i];
        }
        if (preSum > maxRes){
            maxRes = preSum;
        }     
    }
    return maxRes;
}

int maxSubArray(int* nums, int numsSize){
   int result = INT_MIN;
   int count = 0;
   for (int i = 0;i < numsSize;i++){
       count += nums[i];
       if (count > result) {
           result = count;
       }

       if (count < 0) {
           count = 0;
       }
   }
   return result;
}