本文已收录于专栏 《算法合集》

---

---

一、简单释义

1、算法概念

  回溯法，可以系统的搜索一个问题的所有解或任一解。回溯法通常涉及到对问题状态的深度优先搜索，在搜索过程中，算法尝试一步步地构建解决方案，每次决策都会将问题状态转移到下一步，并检查当前状态是否满足问题的要求。如果当前状态满足问题要求，则继续向下搜索；如果不满足要求，则回溯到上一个状态，并尝试其他的决策。

2、算法目的

  回溯法的算法目的是在给定的问题中，通过穷举所有可能的解空间来找到满足问题要求的解。它通常适用于组合、排列、子集、棋盘类等问题，其中每一步都有多个选择，并且需要满足一定的约束条件。

3、算法思想

  回溯法的基本思想是深度优先搜索（DFS），通过递归的方式进行搜索和回溯。

二、核心思想

• 「选择」：在当前步骤中，从可选的选择中选择一个。
• 「验证」：检查选择是否满足问题的约束条件和限制。
• 「递归」：进入下一步骤，继续选择和验证。
• 「撤销」：如果选择不满足问题要求，回溯到上一步，撤销当前选择，并尝试其他选择。

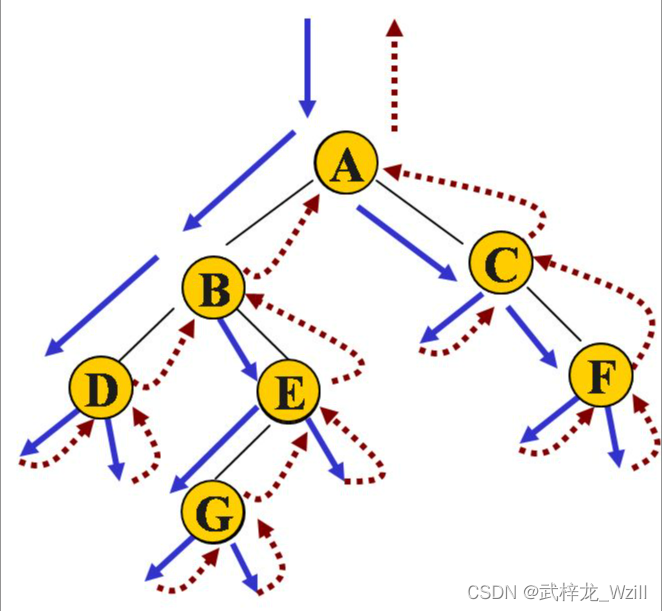
三、图形展示

四、算法实现

1、实现思路

  将图形化展示的过程转换成对应的开发语言，本文中主要以Java语言为例来进行算法的实现。

  1. 首先从根节点开始，对二叉树进行深度优先遍历。
  2. 遍历过程中使用一个字符串构建器 StringBuilder 记录当前路径
  3. 每当遍历到叶子节点时，将当前路径添加到结果列表中，并回溯到上一层节点。

  能把整个过程描述清楚实现起来才会更加容易！！！

2、代码实现

TreeNode 类

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

将数组处理成二叉树结构并且返回根节点

public static TreeNode constructTree(int[] nums) {
    if (nums == null || nums.length == 0) {
        return null;
    }
    // 创建根节点
    TreeNode root = new TreeNode(nums[0]);  
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    int i = 1;
    while (i < nums.length) {
        // 取出队头元素
        TreeNode parent = queue.poll();  
        if (i < nums.length && nums[i] != null) {
            // 创建左子节点
            parent.left = new TreeNode(nums[i]);  
            queue.offer(parent.left);
        }
        i++;
        if (i < nums.length && nums[i] != null) {
            // 创建右子节点
            parent.right = new TreeNode(nums[i]);  
            queue.offer(parent.right);
        }
        i++;
    }
    return root;
}

进行搜索

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        // 用于保存所有从根节点到叶子节点的路径
        List<String> result = new ArrayList<String>();  
        // 处理特殊情况，如果根节点为空，则返回空路径列表
        if (root == null) {  
            return result;
        }
        // 开始深度优先搜索
        dfs(root, new StringBuilder(), result);  
        return result;
    }

    private void dfs(TreeNode node, StringBuilder path, List<String> result) {
        // 如果当前节点为空，返回
        if (node == null) {  
            return;
        }
        // 保存当前路径的长度
        int len = path.length();  
        // 如果当前节点是叶子节点，则将当前路径添加到结果列表中
        if (node.left == null && node.right == null) {  
            result.add(path.append(node.val).toString());
            // 恢复当前路径的长度
            path.setLength(len);  
            return;
        }
        // 将当前节点添加到路径中，并加上箭头
        path.append(node.val).append("->");  
        // 递归遍历左子树
        dfs(node.left, path, result);
        // 递归遍历右子树  
        dfs(node.right, path, result);
        // 恢复当前路径的长度  
        path.setLength(len);  
    }
}

五、算法分析

1、时间复杂度

  回溯法的时间复杂度通常较高，因为它需要穷举所有可能的解空间。在最坏情况下，回溯法的时间复杂度为指数级别，即O(2^n)，其中n为问题的规模。这是因为在每一步中，都有多个选择需要尝试，而每个选择都会导致进一步的递归调用。

2、空间复杂度

  回溯法的空间复杂度取决于递归调用的深度。在每一步中，都会有一部分空间用于保存当前的状态和选择。因此，回溯法的空间复杂度通常是O(n)，其中n为问题的规模。

3、算法稳定性

   回溯法是一种完备性算法，即能够找到所有满足问题要求的解。它通过穷举所有可能的解空间来搜索解，因此在给定的问题中，回溯法能够找到所有可能的解。然而，回溯法的效率和稳定性可能受到问题规模的影响。对于规模较大的问题，回溯法可能会耗费大量的时间和空间。在实际应用中，可以通过剪枝等优化策略来减少搜索空间，提高算法效率。

🎯 此文章对你有用的话记得留言+点赞+收藏哦🎯