目的
深入了解线性回归的使用方法,使用非线性激活函数,同时使用pytorch的nn模块,最后使用神经网络来求解线性拟合,只有深入了解了基础,才能做出更高水平的东西。
上一章 神经网络梯度下降和线性回归
拟合定义数据
以下是随意的数据,不用太在意,我们在使用图像分类的时候,或多或少的使用训练集和验证集,我们也同样如此来做这个事情
下面使用unsqueeze来增加维度
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c).unsqueeze(1)
t_u = torch.tensor(t_u).unsqueeze(1)
接下来我们打乱数据,将数据分成训练集和验证集,但是每个集合都需要分为输入和输出
n_samples = t_u.shape[0]
print(t_u.shape)
n_val = int(0.2 * n_samples)
shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]
t_u_train = t_u[train_indices]
t_c_train = t_c[train_indices]
t_u_val = t_u[val_indices]
t_c_val = t_c[val_indices]
归一化
神经网络里面有一个归一化过程,为什么要用到这个过程?为了让权重的梯度和偏置的梯度在同样的比例空间,否则,优化过程稳定以后,参数收到的更新非常小,损失下降的非常慢,要么数据归一化,要么改变输入。这里我们简单地将输入乘以0.1
t_un_train = 0.1 * t_u_train
t_un_val = 0.1 * t_u_val
print("1 ...",t_u_train)
print("2 ...",t_un_train)
定义训练过程
def training_loop(n_epochs, optimizer, model, loss_fn, t_u_train, t_u_val,
t_c_train, t_c_val):
for epoch in range(1, n_epochs + 1):
t_p_train = model(t_u_train)
loss_train = loss_fn(t_p_train, t_c_train)
t_p_val = model(t_u_val)
loss_val = loss_fn(t_p_val, t_c_val)
optimizer.zero_grad()
loss_train.backward()
optimizer.step()
if epoch == 1 or epoch % 1000 == 0:
print(f"Epoch {epoch}, Training loss {loss_train.item():.4f},"
f" Validation loss {loss_val.item():.4f}")
损失函数
def loss_fn(t_p, t_c):
squared_diffs = (t_p - t_c)**2
return squared_diffs.mean()
以上就是损失函数,实际上就是均方的均值,这个和 nn 模块的一个函数是一样的
nn.MSELoss()
代码清单
**import numpy as np
import torch
import torch.optim as optim
import torch.nn as nn
torch.set_printoptions(edgeitems=2, linewidth=75)
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c).unsqueeze(1) # <1>
t_u = torch.tensor(t_u).unsqueeze(1) # <1>
print(t_c)
n_samples = t_u.shape[0]
print(t_u.shape)
n_val = int(0.2 * n_samples)
shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]
t_u_train = t_u[train_indices]
t_c_train = t_c[train_indices]
t_u_val = t_u[val_indices]
t_c_val = t_c[val_indices]
t_un_train = 0.1 * t_u_train
t_un_val = 0.1 * t_u_val
print("1 ...",t_u_train)
print("2 ...",t_un_train)
def training_loop(n_epochs, optimizer, model, loss_fn, t_u_train, t_u_val,
t_c_train, t_c_val):
for epoch in range(1, n_epochs + 1):
t_p_train = model(t_u_train)
loss_train = loss_fn(t_p_train, t_c_train)
t_p_val = model(t_u_val)
loss_val = loss_fn(t_p_val, t_c_val)
optimizer.zero_grad()
loss_train.backward()
optimizer.step()
if epoch == 1 or epoch % 1000 == 0:
print(f"Epoch {epoch}, Training loss {loss_train.item():.4f},"
f" Validation loss {loss_val.item():.4f}")
def loss_fn(t_p, t_c):
squared_diffs = (t_p - t_c)**2
return squared_diffs.mean()
linear_model = nn.Linear(1, 1) # <1>
optimizer = optim.SGD(linear_model.parameters(), lr=1e-2)
training_loop(
n_epochs = 6000,
optimizer = optimizer,
model = linear_model,
loss_fn = nn.MSELoss(),
t_u_train = t_un_train,
t_u_val = t_un_val,
t_c_train = t_c_train,
t_c_val = t_c_val)**
执行结果
Epoch 1, Training loss 106.3633, Validation loss 21.0176
Epoch 1000, Training loss 2.6151, Validation loss 9.2893
Epoch 2000, Training loss 2.1240, Validation loss 8.1746
Epoch 3000, Training loss 2.1155, Validation loss 8.0348
Epoch 4000, Training loss 2.1154, Validation loss 8.0166
Epoch 5000, Training loss 2.1154, Validation loss 8.0142
Epoch 6000, Training loss 2.1154, Validation loss 8.0141
打印一下参数
print(linear_model.weight)
print(linear_model.bias)
Parameter containing:
tensor([[5.4109]], requires_grad=True)
Parameter containing:
tensor([-16.9935], requires_grad=True)
修改为非线性模型
seq_model = nn.Sequential(
nn.Linear(1, 11),
nn.Tanh(),
nn.Linear(11, 1))
重新进行训练函数,这次使用19000的epochs,梯度下降学习率放小
optimizer = optim.SGD(seq_model.parameters(), lr=1e-3)
training_loop(
n_epochs = 19000,
optimizer = optimizer,
model = seq_model,
loss_fn = nn.MSELoss(),
t_u_train = t_un_train,
t_u_val = t_un_val,
t_c_train = t_c_train,
t_c_val = t_c_val)
print(linear_model.weight)
print(linear_model.bias)
输出如下
Epoch 1, Training loss 171.8674, Validation loss 222.4864
Epoch 1000, Training loss 6.0413, Validation loss 4.0842
Epoch 2000, Training loss 3.7640, Validation loss 0.3214
Epoch 3000, Training loss 2.7283, Validation loss 0.7976
Epoch 4000, Training loss 2.4138, Validation loss 1.1980
Epoch 5000, Training loss 2.3310, Validation loss 1.5010
Epoch 6000, Training loss 2.3085, Validation loss 1.8028
Epoch 7000, Training loss 2.2909, Validation loss 2.1374
Epoch 8000, Training loss 2.2741, Validation loss 2.5010
Epoch 9000, Training loss 2.2233, Validation loss 2.8891
Epoch 10000, Training loss 2.0921, Validation loss 3.2896
Epoch 11000, Training loss 2.0451, Validation loss 3.6949
Epoch 12000, Training loss 2.0332, Validation loss 3.9851
Epoch 13000, Training loss 2.0221, Validation loss 4.2558
Epoch 14000, Training loss 2.0117, Validation loss 4.5177
Epoch 15000, Training loss 2.0019, Validation loss 4.7740
Epoch 16000, Training loss 1.9925, Validation loss 5.0266
Epoch 17000, Training loss 1.9835, Validation loss 5.2766
Epoch 18000, Training loss 1.9747, Validation loss 5.5250
Epoch 19000, Training loss 1.9660, Validation loss 5.7720
Parameter containing:
tensor([[-0.9412]], requires_grad=True)
Parameter containing:
tensor([-0.4798], requires_grad=True)
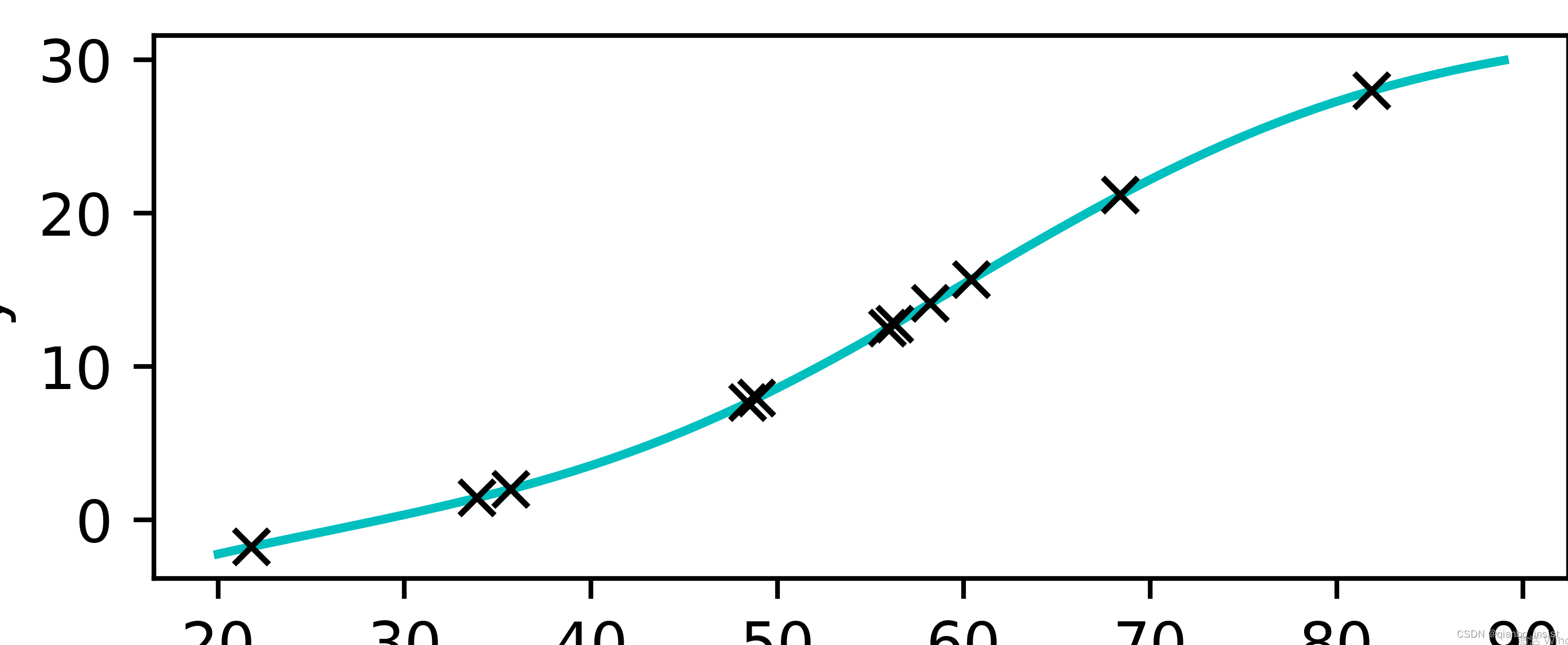
非线性曲线
t_range = torch.arange(20.,90.).unsqueeze(1)
fig = plt.figure(dpi = 600)
plt.xlabel("x)")
plt.ylabel("y")
#plt.plot(t_u.numpy(), t_c.numpy()) # <2>
plt.plot(t_range.numpy(), seq_model(0.1*t_range).detach().numpy(), 'c-')
plt.plot(t_u.numpy(),seq_model(0.1*t_u).detach().numpy(),'kx')
plt.show()
下面画出来,可以看见,非线性比线性要"光滑"了很多