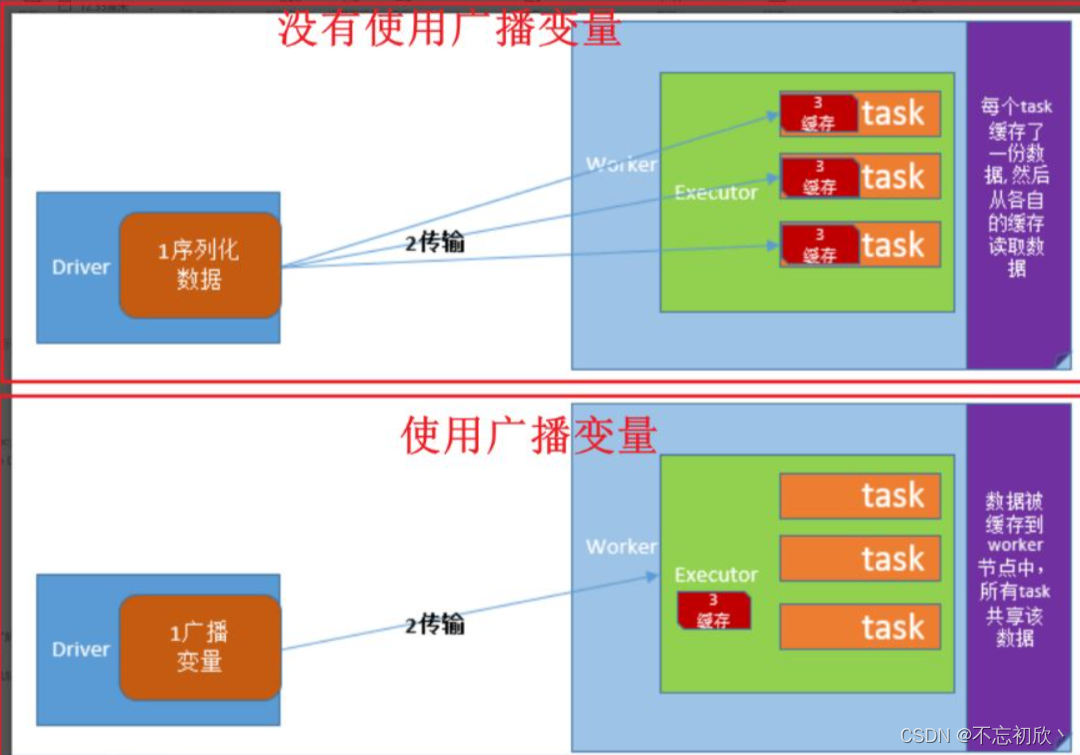
前面阐述过,在设计好一个神经网络后,参数的数量可能会达到百万级别,利用梯度下降去更新参数计算复杂,算力不足,因此需要一种有效计算梯度的方法,这种方法就是辛顿提出的反向传播(简称BP),BP在调整参数时候,不用像以前一样调参,可以先调最后一层,调完最后一层往前调,最后调到最前面一层,这种算法比以前算法复杂度要低得多,使用BP能够使梯度计算时效率更快。
反向传播算法是“误差反向传播”的简称,即BP算法。
BP算法的学习过程由正向传播过程和反向传播过程组成。在正向传播过程中,输入信息通过逐层处理并传向输出层。如果在输出层得不到期望的输出值,则通过构造输出值与真实值的损失函数作为目标函数,转入反向传播,逐层求出目标函数对各神经元权值的偏导数,构成目标函数对权值向量的梯度,作为修改权值的依据,网络的学习在权值修改过程中完成。输出值与真实值的误差达到所期望值时,神经网络学习结束。
1、创建神经网络模型

模型说明
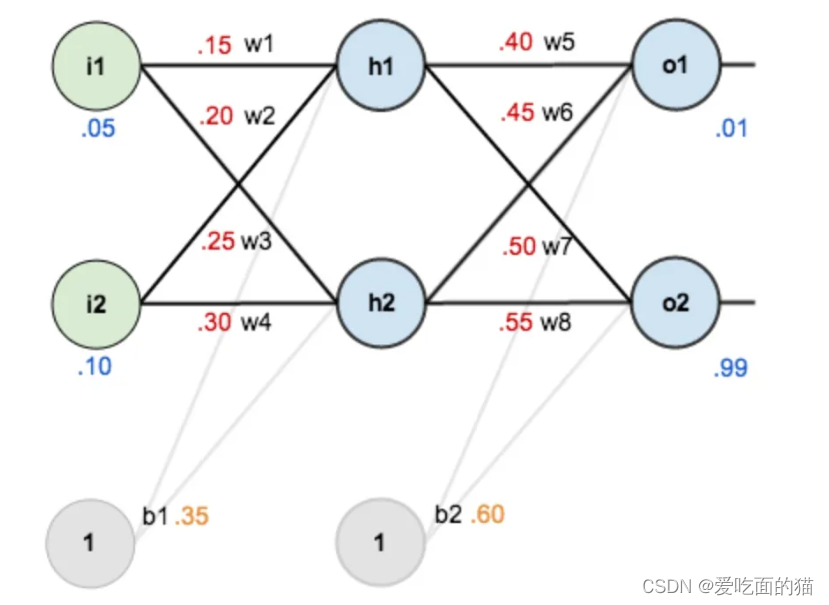
- 模型共三层
- 第一层输入层,包含两个神经元i1,i2和截距b1
第二层隐含层,包含两个神经元h1,h2和截距b2
第三层输出层,包含两个神经元o1,o2
wi是层与层之间连接的权重
激活函数默认为sigmoid函数
执行正向传播
权重赋值
- 输入数据:i1 =0.05,i2 =0.10;
输出数据:o1 =0.01,o2 =0.99;
初始权重:w1 =0.15,w2 =0.20,w3 =0.25,w4 =0.30,
w5 =0.40, w6 =0.45, w7 =0.50, w8 =0.55
目标:给出输入数据 i1 =0.05 i2 =0.10,使输结果出尽可能与原始输出o1 =0.01 o2 =0.99 接近
前向传播,模拟计算

通过前向传播得到输出值为[0.75136079 , 0.772928465],与实际值[0.01 , 0.99]相差还很远,现在对误差进行反向传播,更新权值,重新计算输出。
执行反向传播
见:反向传播(back propagation) - 知乎