这两道题都是方案数问题，注意方案数问题背包是装满的

518.零钱兑换Ⅱ（装满背包方案数，本题是组合方案数）

• 本题就属于完全背包问题，但是for循环不可颠倒的情况。
• 本题求的是组合方案，颠倒for的顺序就是排列方案

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2：

输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。

示例 3：

输入：amount = 10, coins = [10] 
输出：1

提示：

• 1 <= coins.length <= 300
• 1 <= coins[i] <= 5000
• coins 中的所有值 互不相同
• 0 <= amount <= 5000

思路

本题提到了”凑成总和“，也就是从数组coins中选取物品，使得物品总重量和为目标和。

因此我们第一反应还是背包问题。实际上，背包问题就是与得到某个确定的目标和有关的问题。

加上题目描述中说，假设每一种面额的硬币有无限个，因此这属于完全背包。

本题最后返回的结果是可以凑成总金额的硬币组合数，也就是说装满背包一共有多少种方案。这就和 494.目标和 有点像，但是 目标和 是01背包。

本题和纯完全背包的区别在于，纯完全背包是求背包最大价值，而本题是求装满背包方案数。

DP数组含义

DP数组含义是看求的是什么。本题求的是装满背包的方案数，因此dp[j]表示装满容量为j的背包，有dp[j]种方法。

递推公式

本题和01背包的 目标和 基本一样，也属于装满背包方案数目，因此也是同样的递推公式：

dp[j]+=dp[j-coins[i]];//装满背包方案数目问题的递推公式模板

DP数组初始化

和 目标和 那道题一样，求方案数目问题，最重要的就是一开始的初始化，因为所有递推都基于dp[0]。

从DP数组的含义来考虑：

dp[0]含义是容量是0，多少种方案装满，因此dp[0]=1

从递推公式角度考虑：

dp[0]必须1，因为dp[0] = 1是方案类问题递归公式的基础。如果dp[0] = 0 的话，后面所有推导出来的值都是0了。

遍历顺序（重要，不能颠倒）

在纯完全背包问题中，外层是物品还是背包都可以。但是本题，遍历顺序是不能颠倒的。

纯完全背包求得装满背包的最大价值是多少，和凑成总和的元素有没有顺序没关系，有顺序也行，没有顺序也行。

但是，本题要求凑成总和的组合数，元素之间明确要求没有顺序。纯完全背包是能凑成总和就行，凑成总和的方案是否有顺序，不在考虑范围内。但是本题是求凑出来的方案个数，且每个方案个数是为组合数，不能有顺序。

外层物品内层背包的情况

我们假设coins[0] = 1，coins[1] = 5，背包容量amount是6。

for(int i=0;i<coins.size();i++){//物品外层
    for(int j=coins[i];j<=amount;j++){
        dp[j]+=dp[j-coins[i]];
    }
}

对于物品在外，背包在内的情况：

1. 先使用硬币1，计算出所有可能的组合。
2. 然后加入硬币5，计算出所有可能的组合。

遍历物品i的DP数组如下所示：

// 初始化 DP 数组
dp = [1, 0, 0, 0, 0, 0, 0]

// 遍历硬币1
dp = [1, 1, 1, 1, 1, 1, 1]

// 遍历硬币5
dp = [1, 1, 1, 1, 1, 2, 2]

这个过程中，硬币5是在硬币1的基础上加入的，所以不会出现{5,1}这样的情况，只有{1,5}。

外层背包内层物品的情况

for(int j=0;j<=amount;i++){//背包容量外层
    for(int i=0;i<coins.size();i++){
        if(j>=coins[i])
        	dp[j]+=dp[j-coins[i]];
    }
}

对于背包在外，物品在内的情况：

1. 对于每一个背包，都尝试使用硬币1和硬币5来填满背包。
2. 这就意味着在计算一个特定的背包时，可能会有{1,5}和{5,1}两种情况。

推出来的DP数组如下所示：

我们可以看出来，结果确实是不对的，但是dp方法只能给出方案数，并不能把每个方案都打印出来。如果需要打印每个方案，必须使用回溯来解决，例如组合总和系列问题，因为需要打印组成结果，所以必须是回溯。

回溯法的解释：【总结】用树形图和剪枝操作理解完全背包问题中组合数和排列数问题_先遍历物品后遍历背包是组合数_Calculus2022的博客-CSDN博客

对于coins = {1,2}， amount =4，先遍历物品的情况，相当于对先遍历背包的情况进行了剪枝：

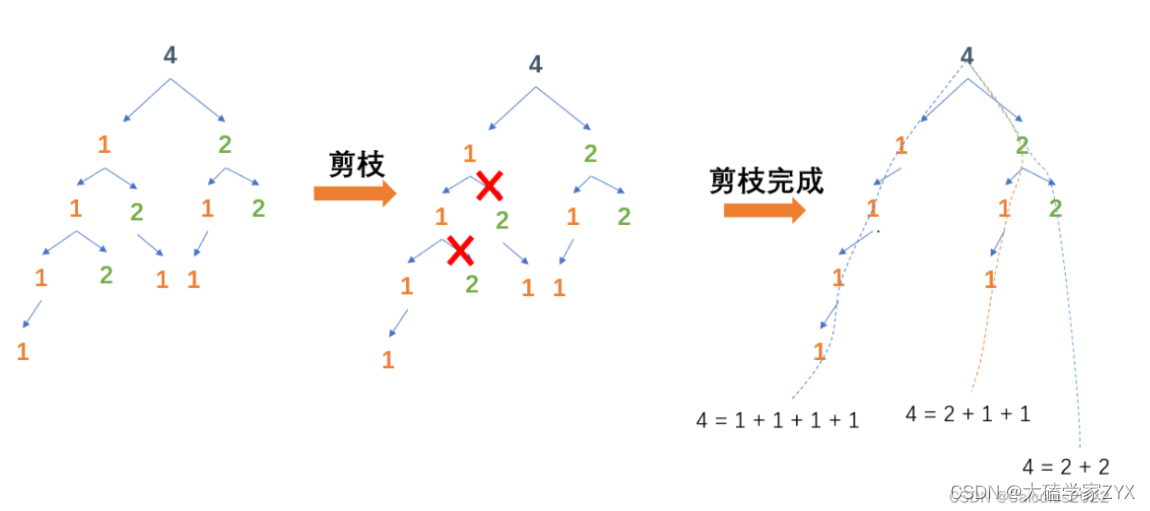
引用这张图能看的更清晰，我们如果先遍历物品，是物品1这条线全部遍历完，物品1遍历的时候不会涉及物品2 ，所以相当于剪枝剪掉了物品1底下1 2那种情况。而到了物品2，拆开2的时候，才会考虑2 1的情况。

由此可知，先遍历物品的情况，相当于对原排列数进行了剪枝。

完全背包求排列数和组合数

完全背包问题中，物品和背包遍历的顺序决定了在求解时是考虑了物品的排列情况还是组合情况。

物品在外，背包在内，得到的是组合方案数目；

物品在内，背包在外，得到的是排列方案数目。

完整版

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        //定义dp数组
        vector<int>dp(amount+1,0);
        //初始化
        dp[0]=1;
        for(int i=0;i<coins.size();i++){
            for(int j=coins[i];j<=amount;j++){
                dp[j]+=dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
};

总结+面试题目

完全背包问题，在求装满背包有几种方案的时候，认清遍历顺序是非常关键的。

如果求所有装满背包方案的组合数，就是外层for循环遍历物品，内层for遍历背包。

如果求所有方案的排列数，就是外层for遍历背包，内层for循环遍历物品。

01背包因为物品和背包遍历顺序不能颠倒，所以并不存在排列数和组合数的问题。

如果面试问到for嵌套顺序颠倒计算排列数和组合数的原理，可以这么回答：

物品在外的话，必须考虑完 i 的所有情况之后再考虑 i + 1，所以去掉了他们的排列关系； 而容量在外的话，每个容量的循环中可以尝试所有的物品，就像排列数每个位置可以放任何物品一样，这样就增加了物品的顺序

377.组合总和Ⅳ（本题是排列方案数）

• 本题需要注意修改Int溢出的问题，dp[j]+=dp[j-nums[i]]可能会发生溢出，此时我们需要让运算结果对一个较大的数字来取模，把dp[j]控制在这个较大数字的范围内。

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

示例 1：

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

示例 2：

输入：nums = [9], target = 3
输出：0

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 1000
• nums 中的所有元素 互不相同
• 1 <= target <= 1000

思路

本质是本题求的是排列总和，而且仅仅是求排列总和的个数，并不是把所有的排列都列出来。为此，我们可以使用完全背包DP来解决。

如果本题要把排列都列出来的话，只能使用回溯算法暴力搜索。像39.组合总和 40.组合总和Ⅱ 都是必须列出组合结果，因此只能用回溯。

之前的组合系列：

39.组合总和：（这道题如果求方案数目是完全背包，且为组合数，物品在for外层）

40.组合总和Ⅱ：（这道题求方案数目是01背包）

DP数组含义

本题从示例可以看出，每个数字可以被使用无限次，所以是完全背包。

dp[j]的含义是，装满容量为j的背包，有dp[j]种方案。

递推公式

本题依然是方案数目的递推公式：

dp[j]+=dp[j-nums[i]];

初始化

方案数目类，初始化都是dp[0]=1,其余为0

遍历顺序

本题是求排列方案数目而不是组合，完全背包求排列方案数，背包外层遍历，物品内层遍历。

具体原因上一道题目有分析。

最开始的写法：int溢出

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<int>dp(target+1,0);
        dp[0]=1;
        //求排列数，外层背包容量
        for(int j=0;j<=target;j++){
            for(int i=0;i<nums.size();i++){
                if(j>=nums[i])
                    dp[j]+=dp[j-nums[i]];
            }
        }
		return dp[target];
    }
};

debug测试

测试结果出现了dp[j]+=dp[j-nums[i]];这一句，两数相加超过了int的情况。

防止溢出的方式：对较大的数字取模

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<long long>dp(target+1,0);
        dp[0]=1;
        long long MOD = INT_MAX; // adding modulo constant
        for(int j=0;j<=target;j++){
            for(int i=0;i<nums.size();i++){
                if(j>=nums[i]) {
                    dp[j]=(dp[j]+dp[j-nums[i]]) % MOD;
                }
            }
        }
        return dp[target];
    }
};

MOD取模的作用

这里注意，我们设置一个MOD，对MOD进行取模，目的就是把结果限制在<=MOD的范围内。

因为取模运算，比如a/b，如果a<b的话，得到的就是a本身。如果a>b，得到的就是a/b的余数。

也就是，如果a=INT_MAX+1，b=INT_MAX，那么a%b就=1。

因此取模运算%，是一个限制数据范围的重要方法，它能保证结果始终在一定范围内。

如果我们想把结果限定在MOD范围内，我们只需要result%MOD即可。

总结

求装满背包有几种方法，递归公式都是一样的，没有什么差别，但关键在于遍历顺序！

本题与518.零钱兑换II就是一个鲜明的对比，一个是求排列，一个是求组合，遍历顺序完全不同。

同时，本题的取模运算也是一个非常重要的点，为了保证dp[j]不溢出，我们令MOD=INT_MAX，然后dp[j]%MOD，就可以让dp[j]限制在INT_MAX范围内。

这个操作和螺旋矩阵里面的(t+1)%4操作很像，螺旋矩阵中t初始值为0，t=(t+1)%4能让无论多大的t，都在0 1 2 3这四个数字里面循环取值。要特别注意这种用法。（t只需要赋初值，别的都不需要管）

[螺旋矩阵题目的两种解法及注意点_大磕学家ZYX的博客-CSDN博客](