目录
💥1 概述
📚2 运行结果
🎉3 参考文献
👨💻4 Matlab代码
💥1 概述
通过GWO(Grey Wolf Optimization)算法对8个发电机进行最佳调度编码是一种优化问题的解决方法。GWO算法灵感来源于灰狼的群体行为,它模拟了灰狼群体中的领导者与追随者之间的协作和竞争关系。以下是该过程的一般步骤:
初始化种群:生成一定数量的随机解,每个解代表一种发电机的调度编码,形成初始的灰狼群体。
计算适应度:对于每个解,计算其适应度值,该值可以是根据问题的特定目标函数计算得出的。
更新领导者:根据适应度值,选择群体中的优秀解作为领导者,并更新其位置。
更新追随者:根据领导者的位置和距离,更新其他灰狼的位置,以模拟协同和竞争的行为。
达到停止条件:重复步骤3和步骤4,直到满足停止条件,例如达到最大迭代次数或达到特定的适应度阈值。
输出最优解:根据停止条件,确定最佳调度编码,即最优解。
GWO算法通过模拟灰狼的行为来进行全局搜索和优化,它可以用于解决各种优化问题,包括发电机调度问题。通过调整算法的参数和目标函数的设定,可以根据具体的发电机调度问题进行定制化的应用。
需要注意的是,GWO算法是一种启发式算法,其结果可能会受到初始参数和停止条件的影响。为了得到更可靠的结果,可以进行多次运行,并对最终的最优解进行统计分析和验证。
📚2 运行结果
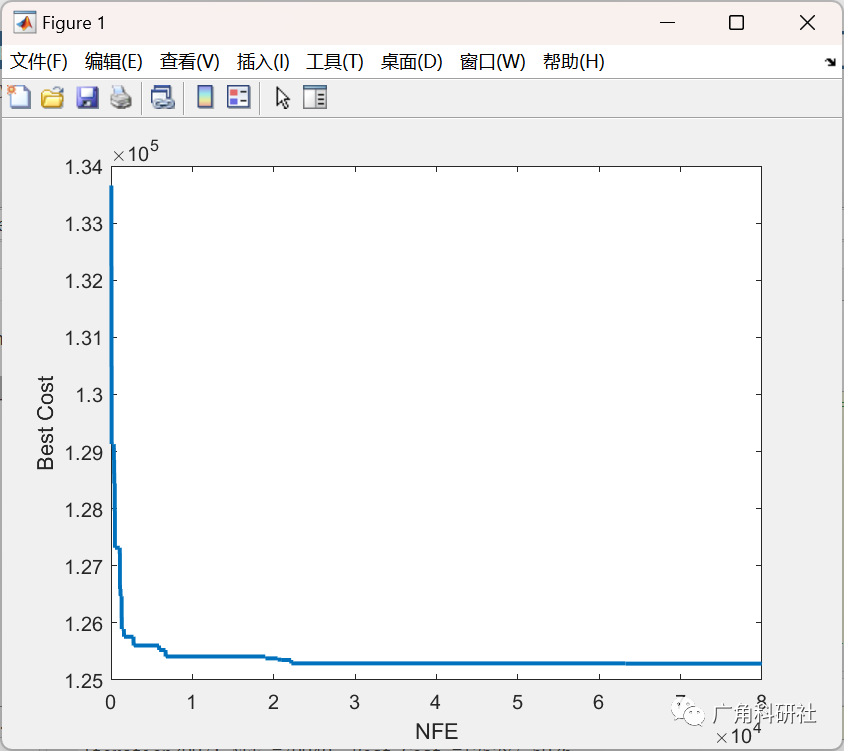
主函数部分代码:
clear
clc
%% Problem Definition======================================================
global NFE
NFE=0;
model=CreateModel();
CostFunction=@(p) MyCost(p,model); %Cost Function
nVar=model.N; %No. of Variables
VarSize=[1 nVar]; %Size of Decision Variables Matrix
% VarMin=-10; % Lower Bound of Variables
% VarMax=10; % Upper Bound of Variables
VarMin=model.pmin; % Lower Bound of Variables
VarMax=model.pmax; % Upper Bound of Variables
%% Algorithm Settings======================================================
MaxIt=4000; % Maximum Number of Iterations
nPop=20; % Population Size (Swarm Size)
% initialize alpha, beta, and delta_pos
Alpha_pos=zeros(1,nVar);
Alpha_score=inf; %change this to -inf for maximization problems
Beta_pos=zeros(1,nVar);
Beta_score=inf; %change this to -inf for maximization problems
Delta_pos=zeros(1,nVar);
Delta_score=inf; %change this to -inf for maximization problems
BestCost=zeros(MaxIt,1);
nfe=zeros(MaxIt,1);
%% Initialization==========================================================
empty_particle.Position=[];
empty_particle.Cost=[];
empty_particle.Sol=[];
% empty_particle.Velocity=[];
% empty_particle.Best.Position=[];
% empty_particle.Best.Cost=[];
% empty_particle.Best.Sol=[];
particle=repmat(empty_particle,nPop,1);
% GlobalBest.Cost=inf;
for i=1:nPop
% Initialize Position
particle(i).Position=CreateRandomSolution(model);
end
%% Main Loop===============================================================
l=0;% Loop counter
while l<MaxIt
for i=1:nPop
% Apply Position Limits
particle(i).Position = max(particle(i).Position,VarMin);
particle(i).Position = min(particle(i).Position,VarMax);
% Evaluation
[particle(i).Cost,particle(i).Sol] = CostFunction(particle(i).Position);
% Update Alpha, Beta, and Delta
if particle(i).Cost<Alpha_score
Alpha_score=particle(i).Cost; % Update alpha
Alpha_Sol=particle(i).Sol; %Storing the results
Alpha_pos=particle(i).Position;
end
if particle(i).Cost>Alpha_score && particle(i).Cost<Beta_score
Beta_score=particle(i).Cost; % Update beta
Beta_pos=particle(i).Position;
end
if particle(i).Cost>Alpha_score && particle(i).Cost>Beta_score && particle(i).Cost<Delta_score
Delta_score=particle(i).Cost; % Update delta
Delta_pos=particle(i).Position;
end
end
a=2-l*((2)/MaxIt); % a decreases linearly fron 2 to 0
% Update the Position of search agents including omegas
for i=1:nPop
for j=1:nVar
r1=rand(); % r1 is a random number in [0,1]
r2=rand(); % r2 is a random number in [0,1]
A1=2*a*r1-a;
C1=2*r2;
D_alpha=abs(C1*Alpha_pos(j)-particle(i).Position(1,j));
X1=Alpha_pos(j)-A1*D_alpha;
r1=rand();
r2=rand();
A2=2*a*r1-a;
C2=2*r2;
D_beta=abs(C2*Beta_pos(j)-particle(i).Position(1,j));
X2=Beta_pos(j)-A2*D_beta;
r1=rand();
r2=rand();
A3=2*a*r1-a;
C3=2*r2;
D_delta=abs(C3*Delta_pos(j)-particle(i).Position(1,j));
X3=Delta_pos(j)-A3*D_delta;
particle(i).Position(1,j)=(X1+X2+X3)/3;
end
end
🎉3 参考文献
[1]李淼. 灰狼算法在典型车间调度问题中的应用研究[D].昆明理工大学,2017.
部分理论引用网络文献,若有侵权联系博主删除。