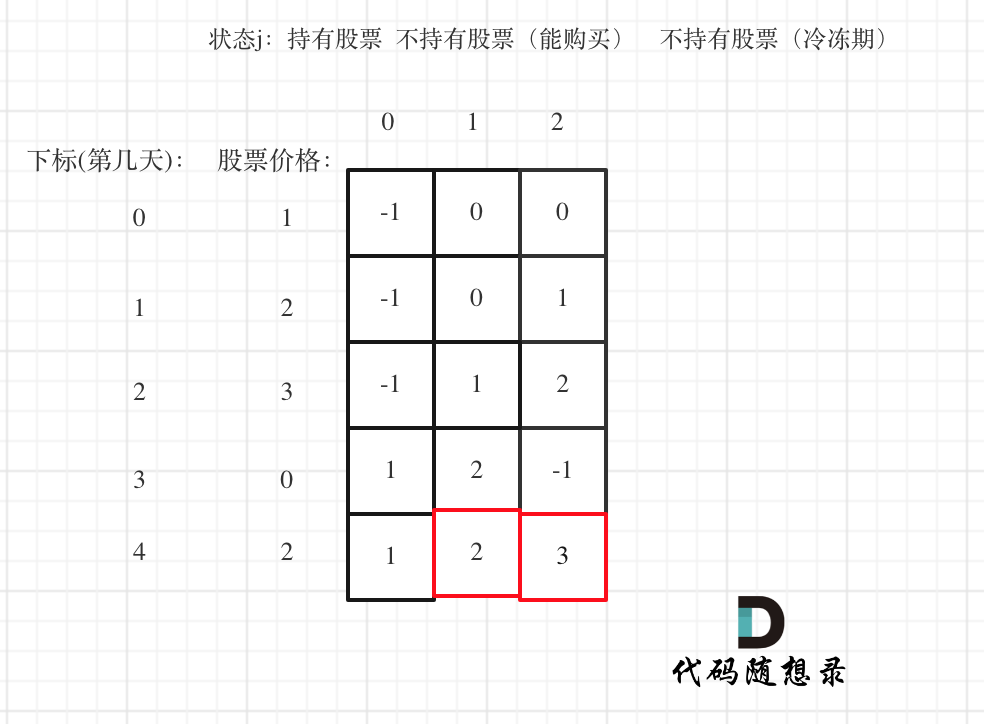
题目描述：写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：F(0) = 0,   F(1) = 1，F(N) = F(N - 1) + F(N - 2), 其中 N > 1.斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。对于青蛙普通跳台阶，和斐波那契数列一样，只是初始值不同， f(0) = 0,  f(1) = 1, f (2) = 2。

 

分析：

        递归法，直接利用递推公式，进行递归，退出条件为 F(0) = 0,   F(1) = 1。

        迭代法，使用两个变量存储前两个数的值，从 1 到n - 1 个遍历即可。

        公式法，经过递推公式计算，数列的通项公式为：

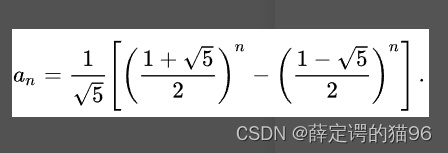
其中 是黄金分割比。

求解：

// 递归法
function fib1(n: number): number {
  if (n < 0) {
    throw new Error('the input number is invalid');
  }
  if (n < 2) {
    return n;
  }
  const mod = 1000000007;
  return (fib1(n - 1) + fib1(n - 2)) % mod;
}

// 动态规划迭代法
function fib2(n: number): number {
  if (n < 0) {
    throw new Error('the input number is invalid');
  }

  if (n < 2) {
    return n;
  }
  let a = 0;
  let b = 1;
  let res = 0;
  const mod = 1000000007;
  for (let i = 1; i < n; i++) {
    res = (a + b) % mod;
    a = b;
    b = res;
  }
  return res;
}

// 公式法
function fib3(n: number): number {
  if (n < 0) {
    throw new Error('the input number is invalid');
  }
  const rootOfFive = Math.pow(5, 0.5);
  const goldenRatio = (rootOfFive - 1) / 2;
  const mod = 1000000007;
  return Math.floor(Math.pow(1 + goldenRatio, n) - Math.pow(-goldenRatio, n) / rootOfFive) % mod;
}