SOCVPOCV、global/local variation

news2024/11/27 12:47:56

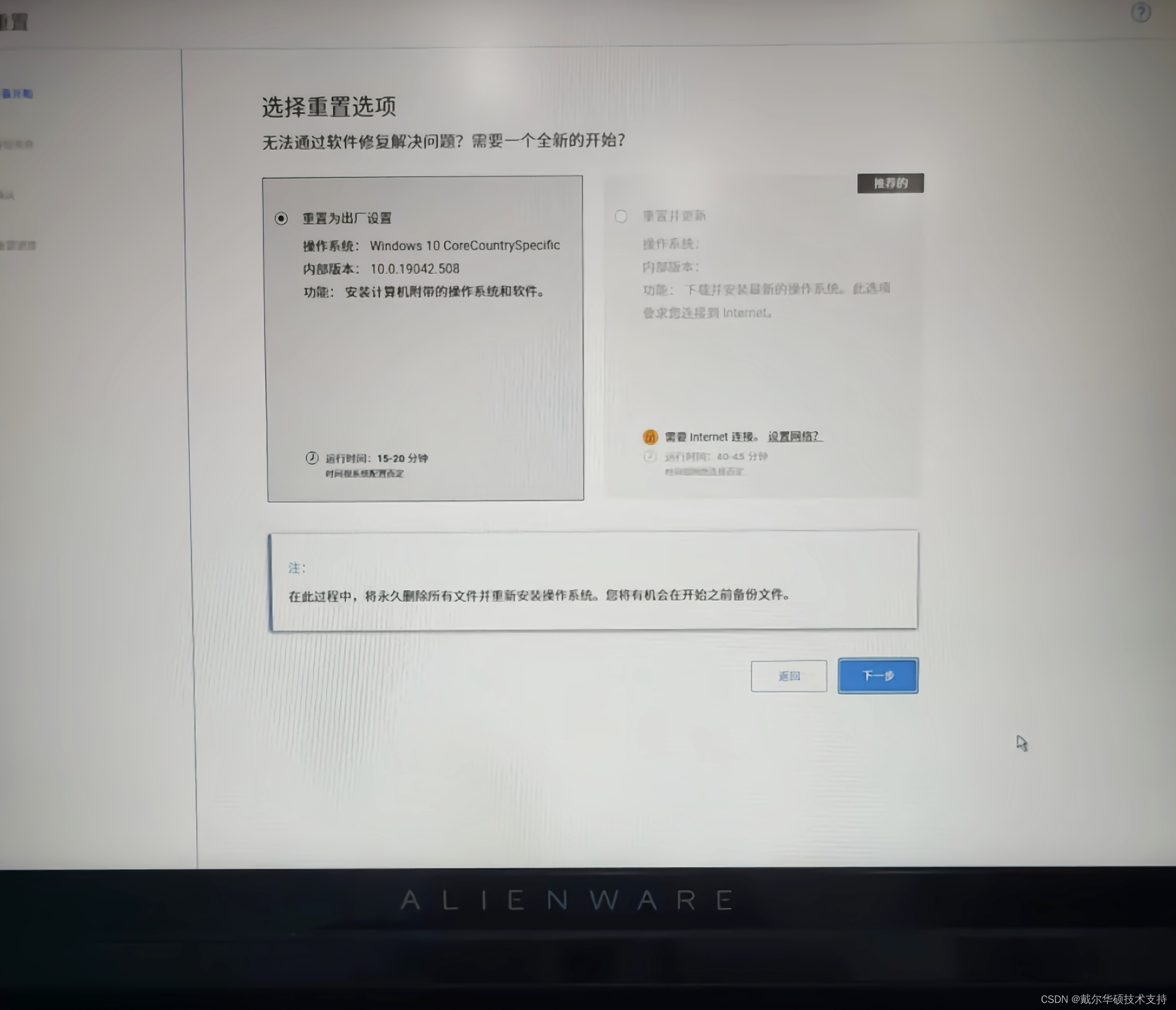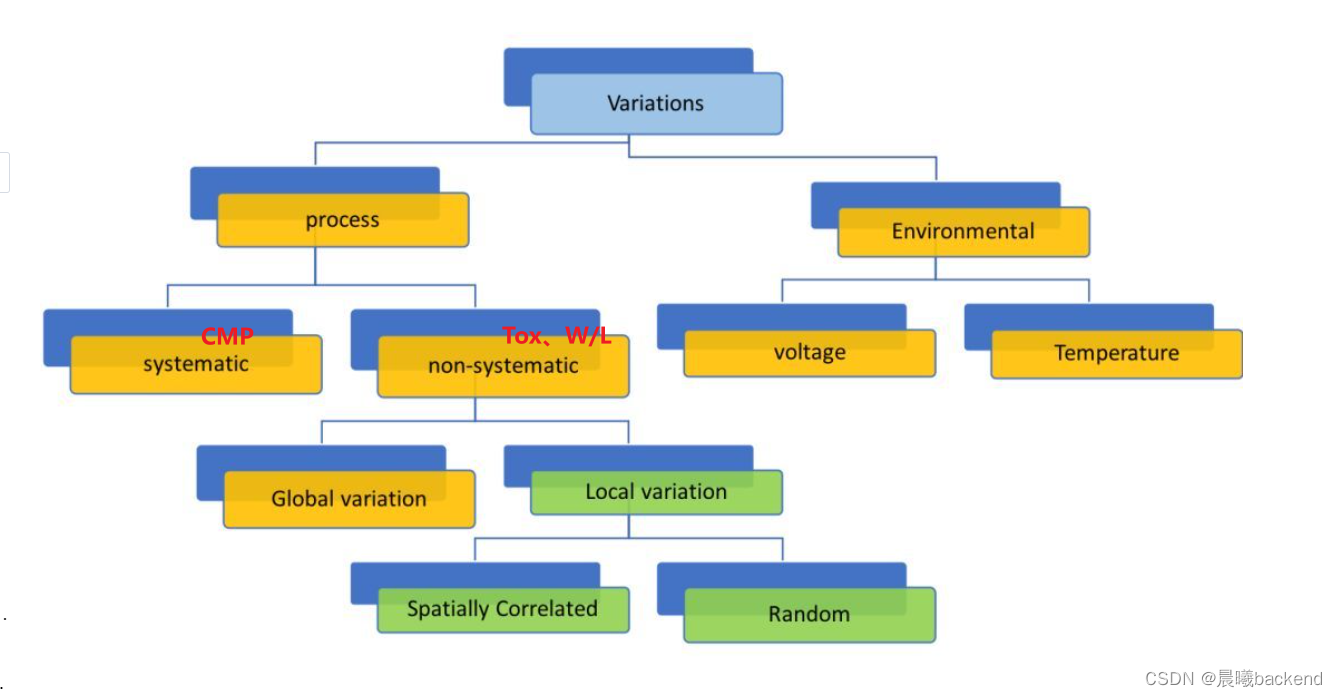
在这里插入图片描述

Global/local variation

global variation 用PVT 跟 RC-corner 来模拟；local variation 用 OCV/ AOCV/ SOCV 来模拟。在40nm 之前OCV 被广泛采用，但是OCV 对同一条path 上的所有cell 都设同一个derate 值，如果设的太严则过于悲观，如果设得太松又会导致过多的path 过于乐观，进入28nm 之后尤其是16nm 之后，OCV 模型越来越"力不从心"，于是有了AOCV 模型。

Global variation: 由于工艺偏移导致的die-to-die, wafer to wafer, lot to lot 之间偏差，如：同一个chip上所有管子的沟道长度都比典型值偏大或偏小
- Delay corner（PVT 和RC corner）用于模拟Global varition
- STA 用RC corner来模拟互连线的variation
Local variation (within-die or intra-die): 同一芯片上不同管子受工艺偏差影响不同< 注：on chip variation 之源>，如：同一芯片上有些管子的沟道长度偏小，而有些管子的沟道长度却偏大。显然，local variation 比 global variation 小

为了模拟工艺偏差对芯片性能的影响，引入了On chip variation模型，40nm 之前简单的flat derate模型基本可以覆盖大部分情况，且不过于悲观到不能接受。但进入40 nm 之后flat derate（ocv）已不再是一个有效的模型，所以引入了更复杂的AOCV (Advanced OCV) 模型，考虑depth 跟 distance的影响（但还是悲观了一点点）。

此时AOCV table的背后已有统计学的支撑，即所谓的SSTA (statistical staic timing analysis).。但限于runtime 当今STA 默认都是基于GBA (Graph Based Analysis) 进行timing 分析，这就使得stage（选择cell所在的所有timing path中最小的stage所在的timing path---Minimum stage count per instance is used for all paths (pessimistic)）和distance（一条timing path所在物理范围的对角线长度）的计算并不精确，从而导致过于悲观，如果用PBA (Path Based Analysis) 方式来计算,runtime又不能接受。

于是进入16nm 之后，一种新的OCV模型开始被广泛使用，C家称之为SOCV (statistical OCV), S家称之为POCV (Parametric OCV), 除了名字的差别，背后都是统计学都是正态分布，背后的算法也基本一致。因为SOCV / POCV 不再是简单的设一个derate 值（OCV）或查一个表格（AOCV/SBOCV），而是要做一系列概率计算（正态分布，normal delay cell数量偏多，increase/decrease delay cell 数量偏少）。

做SOCV / POCV STA 分析时，需要有描述derate 值的LVF 文件，通常LVF 文件由foundry 提供，liberty variation format是一种和liberty库文件（.lib）有关的数据格式。

基本概率知识

随机变量分离散随机变量和连续随机变量，芯片制造过程中的工艺偏差属于连续随机变量范畴，所以在进入SOCV / POCV 之前，先来理解几个概念：随机变量、概率函数、累积分布函数、概率密度函数、均值、方差。

随机变量 (Random Variable)

在现实世界中，许多量是无法准确预测的，故经常使用随机变量来表示，如管子的阈值电压、工艺偏差（channel W/L 、Thickness of oxide）等

概率函数 (Probability)

如果运行大量测试，会发现随机变量的值通常遵循一定规律。随机变量处于x的可能性称为概率，通常用P(x) 表示
在这里插入图片描述

概率密度函数 (ProbabilityDensity Function)

用于描述随机变量落在特定值范围内的概率，这个概率为概率密度函数在这个区域上的积分。如下图，该随机变量落在-1σ ~ 1σ间的概率是68.27%。SOCV / POCV 中sigma的取值，就是根据这个概率得来，所取sigma 的值需要保证大部分情况可以被覆盖到。

均值 (mean)、方差 (Sigma σ、随机变量与平均值的偏差程度)

在这里插入图片描述

正态分布 (Normal distribution) 也称高斯分布 (Gaussian distribution);

对于正态分布，随机变量落在-1σ ~ 1σ间的概率是68.27%，落在-2σ ~ 2σ间的概率是95.45%，落在-3σ ~ 3σ间的概率是99.73%。这也是为什么SOCV / POCV 取3σ 的原因所在。
在这里插入图片描述

OCV、AOCV/SBOCV局限性

local varition 本就是个正态分布，所以SSTA 可以近乎精确地对其进行模拟。然而由于SSTA 的复杂性，基本在正式工程应用中无法落地，所以这么些年来，都还是在传统STA 模型上做精化，而精化的重头戏之一就是On chip variation。从OCV 到AOCV/SBOCV 到SOCV / POCV, 逐渐的加入更多因素，以得到更精确的模拟**（用OCV模拟local variation对 delay/timing的影响）**。

下图为late derate

OCV: 同一个corner 同一段path 上的所有cell 用一个derate 值；不考虑path 的depth 跟 distance, 也不考虑cell 的类型。所以结果对大部分path 而言过于悲观，而对另一小部分path 而言又过于乐观

在这里插入图片描述

AOCV: 即所谓的stage based OCV (SBOCV), 将derate 模拟成path depth 跟 distance 的函数，所以对同一段path 上不同depth、不同distance的cell 有不同的derate 值, 所以相较于OCV 更精确，但是AOCV 有两个局限：一是没有考虑cell 的trantion 跟 load 对variation 的影响，也没有考虑transition 的variation；二是GBA模式下计算得到的逻辑级数和distance 过于悲观，而PBA runtime 又难以接受。

在这里插入图片描述

SOCV/POCV（statistical/parametric）

SOCV / POCV: 统计OCV 是一种使用单一local variable 的SSTA 简化模型，对每个cell 分别建模，cell 的derate 不再是path depth 的函数，而是一个基于单一 µ(均值) 和σ(方差) 的高斯随机变量函数。

SOCV / POCV 可以弥补AOCV 的局限，它考虑cell 的transition 跟 load 对variation 的影响，也考虑variation 对cell transition 的影响；由于其不依赖于depth, 所以也不受depth 精度的影响。

POCV，又称SOCV(Statistical On Chip Variation)，如下图所示，POCV将delay模拟成一个正态分布N(u,sigma )。每个cell的delay最高概率出现在 u周围。整体落在正负3sigma区间内的概率为99.7%

在这里插入图片描述

POCV / SOCV具有如下特点：
- 每一级delay 都是一个(µ,σ) 的分布，时序分布作为独立的随机变量通过时序图传播
- 每个cell / net 的variation 都用统计参数表示
- variation 是输入transition 跟输出load 的函数
- 更精确，跟SPICE 仿真结果的correlation 更好
- timing report 中delay 值用µ + n*σ 表示，默认n 是3，即通常所说的3 sigma
  - 落在-3σ ~ 3σ <即3 sigma > 间的概率是99.73%. 由此可知3 sigma 可以保证99.73 的情况都可以被覆盖到，所以当前最先进工艺仍用3 sigma 来卡。

目前，SOCV 可以三种形式呈现

Timing lib 中带有LVF data, T 家先进工艺的库大多以这种形式呈现，LVF data 集成在timing lib 中，每个timing arc 都有 early/ late 的 ocv_sigma* 和LVF moment 表格，表格的纵坐标是输入pin 的slew, 表格的横坐标是输出pin 的load.

独立的LVF data, 其内容同timing lib 中集成的LVF data 一样。
没有SOCV data, 需要基于AOCV 的table 抽取SOCV data.
- 在没有LVF 时，可以用AOCV table 抽取一个SOCV sigma 值用于简单非精确分析，除此之外对于SOCV 如果使用Cadence 工具也可以使用SOCV library format（variation on Delay/Slew/Checks(setup/hold)）
- 精度不够，不足以用于sign off. 因为AOCV 只有对delay 的variation, 所以无法从AOCV lib 中抽出transtion 跟constraints 的variation