目录

一.总结

二.l的方向余弦

三.方向导数

四.方向导数和方向余弦的联系

五.梯度

1.定义

2.性质

3.运算公式

4.例题 

六.最快下降法

---

一.总结

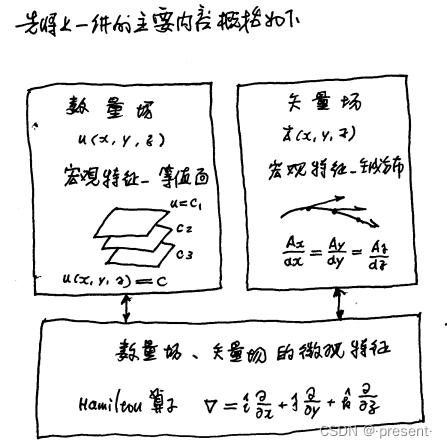
上一节我们研究了数量场和矢量场的宏观特征，但宏观特征，在细节上往往无法展现事物的真正全

貌，所以这节我们会从数量场的微观特征出发，同时引入算子的概念. 

二.l的方向余弦

上一节，我们研究了数量场中不变的量——等值面，但是这是远远不够的.

从一个等值面移动到另一个等值面，移动的方向可能是不同的.

一个小球运动10m，朝下运动，和朝上运动

如果单纯只看数值10m，那这两种情况就是相同的.

但显然这是两种不同的情况

在空间数量场u(x,y,z)的某点，我们允许该点向各个方向作出变化的，因此，变化方向是数量场研

究的独有特色.

谈及方向，我们自然而然可以想到，向量也是具有这一特征的.

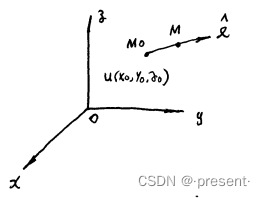
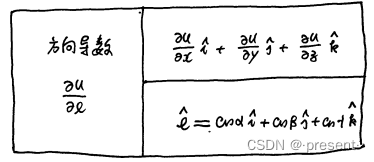
在空间场u = (x,y,z)的空间中取一定点M0，在M0处，我们可以朝任意一个方向变化，而这个方向，

我们可以用一个矢量来表示

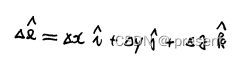
很好理解，实际上就是在x,y,z这三个分量上的增量所构成的矢量

不过，我们并不想要矢量的大小，而仅仅需要其代表方向即可，所以，我们要取它的单位矢

想要求单位矢，就用这个矢量，除以对应矢量的大小即可.

得到的这个单位矢，就是我们所需要的，能够代表变化方向的量

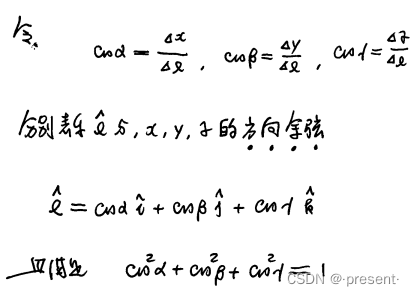
实际题目会给出一个具体的矢量，想要求解这个矢量对应的方向余弦

问题其实对应就是求解它的单位矢

为什么叫方向余弦呢？方向我们已经明白，余弦是由于它的每一个分量，实际都是一个以对应分

量(x,y,z的坐标值)为直角边，斜边为矢量大小的一个直角三角形，所求解的余弦值.

三.方向导数

单纯研究变化量，还是远远不够的，就像研究速度变化一样，想要研究速度的变化，还需要研究速

度的变化快慢，也就是加速度

同样，如果说等值面是数量场的宏观特征，那我们还需要进一步研究数量场的微观特征——某一点

沿某一个方向的变化率.

类比于二维导数的定义，来定义方向导数

和我们之前熟知的二维导数对比，分子都是变化量，但分母有所区别

二维导数的分母是dx(当x无限逼近于0)，方向导数的分母则是无限逼近M0M的一段长度dl(当M点无

限逼近于M0点)

由于分母恒大于0

当方向导数大于0时，对应的是沿该方向的变化量增加

方向导数小于0时，对应的是沿该方向的变化量减小

等于0时，对应l方向处于等值面上，此时变化量为0；或者换句话说，等值面上，数量场u的方向导

数为0

四.方向导数和方向余弦的联系

可以直接给出下面的这个定理，建立起方向导数和方向余弦之间的关系 

证明如下：

五.梯度

1.定义

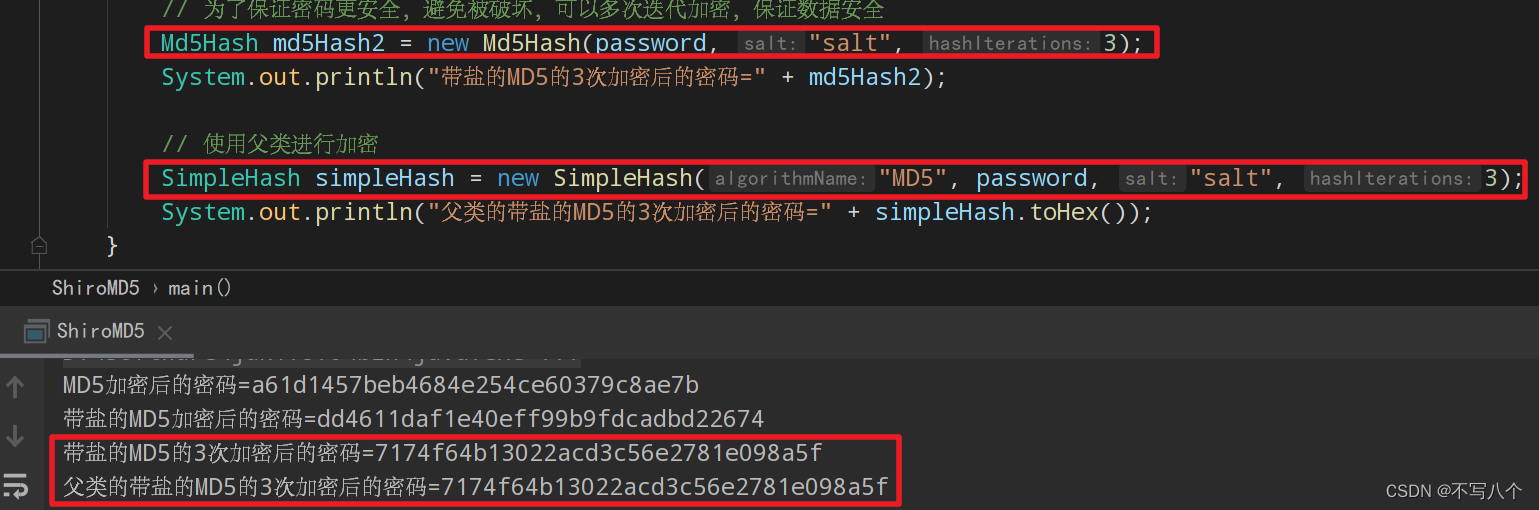
方向导数是什么？本质上就是一个算出来具体的数

而上面定理得到的等式，右边是两两相乘的数

于是我们就可以联想到点积的定义

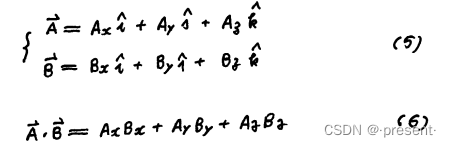
将左边方向导数，看作是两个矢量的点积

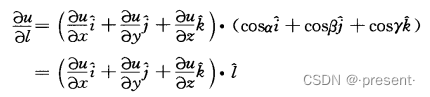
这一步非常重要，它清晰地表明了一个事实，数量场的方向导数由两部分组成，一个是所取方向的

单位余弦；第二个是数量场的导数矢 ，我们把这个数量场的导数矢称为梯度.

但更重要的是，它将变化和方向拆解开了

梯度即是变化，是数量场在某一个定点M0的固有特性，和方向(单位余弦)是没有任何关系的

 但这样一个简单的步骤(将其看作是两个矢量的点积)所起的作用还远远不局限于此

我们引入Hamiltou算子，一个▽符号

梯度就可以简单写为下面的表述形式

方向导数也可以进一步写为一个很简单的形式

后面我们将会看到算子引入的作用，除了将形式化简，还有将运算和对象分开的作用 

对象可以是数量场，那可不可以是矢量场呢？

运算可以是点积，那算子和对象能否做叉积运算呢？

2.性质

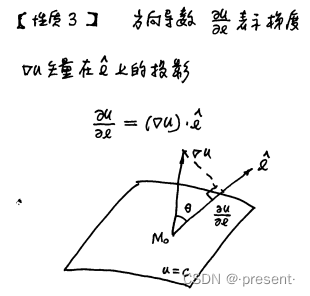
梯度是一个矢量，研究它的性质，实际上就是研究它的大小和方向，还有抓住梯度和方向导数两

者之间的关系 

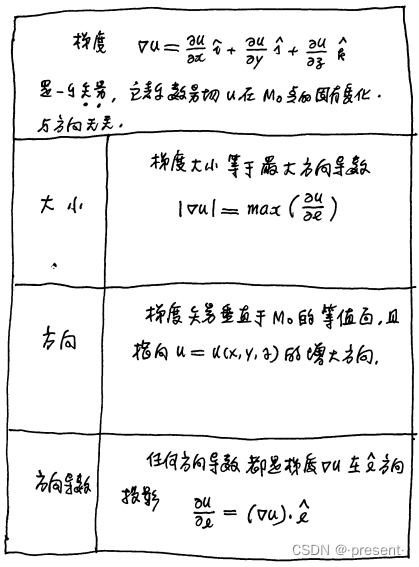
性质1. (大小)

点积的几何意义是投影，一个矢量向另外一个矢量做投影

那我们知道一旦我们确定数量场的某一个定点M0，我们就确定了该点的梯度

梯度是数量场在某一个定点M0的固有特性，也就是一个定矢量

因此，方向导数何时取到最大值？

其实就是方向余弦指向的方向和梯度作为矢量指向的方向重合的时候，方向导数取到最大值

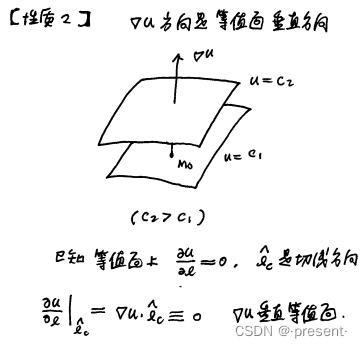
性质2.(方向)

前面我们已经指出

等值面上，数量场u的方向导数为0

我们又知道，等值面上的方向余弦方向，实际上就是定点M0沿等值面的切线方向

两个矢量点积，最终得到的结果为0，从几何上看，就是两个矢量相互垂直

因此，梯度的方向始终垂直于于定点M0的等值面，并指向函数的增大方向

性质3.(与方向导数之间的关系)

3.运算公式

梯度，在运算时，实际上就是对数量场的每一个分量进行求导，得到一个矢量

那符合求导的性质，实际上也符合梯度的运算公式

PS：

1.常矢量的梯度为0

2.常数可以从算子中提出

3.两个矢量点积得到的是数量场，因此可以对两个矢量的点积求梯度

4.复合函数的梯度，也满足链式法则(最后一条)

4.例题 

 矢径的长度是一个数量场，它的梯度是单位矢

六.最快下降法

梯度在实际应用也非常广泛，比如说爬山问题

从山顶要按怎样的路线，最快到达相应的山谷呢？

一个最优的算法，就是每次按梯度的方向走，因为梯度指向的方向，变化率最大

每次局部最优，变化最快，自然累积起来，就能最快的到达山谷

这里就以二元函数为例作出讨论

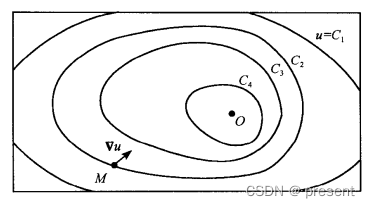
 我们的目标是求解minF(x,y),设起始点为(x0,y0)，第1步移动到的位置，就是初始位置表示的矢量

与梯度代表的矢量作差，类似可以推广到第i+1步

 为了使ki最佳，实际就是求导，使其等于0来求解

举一道具体的例子

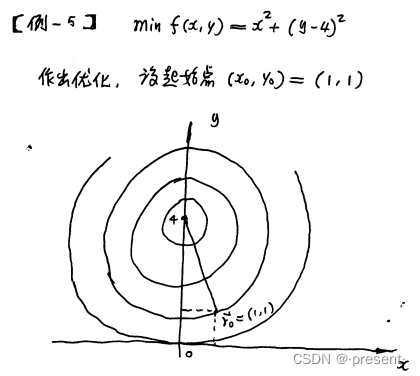
现在我们从起始点(1,1)出发，然后求解按照怎样的路径能够最快到达，minf(x,y)的位置

由表达式可以得知，minf(x,y)的位置为(0,4)

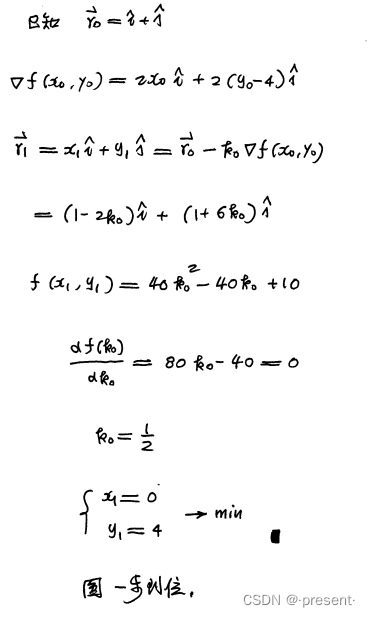
 不过并非总能一步到位，这里能够一步到位，直接求出移动路径，主要是由于这是一个对称的圆