目录
1.1 二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段编辑
1.2 堆的概念及应用
堆的性质:
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
编辑
编辑如图所示就是小根堆和大根堆的展示
2. 堆的代码及实现
2.1 向下调整和向上调整
这里面我们这期主要就讲解两种方法:向下调整,向上调整这两种方法
代码实现:
1.1 二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段

1.2 堆的概念及应用
堆就是以二叉树的顺序存储方式来存储元素,同时又要满足父亲结点存储数据都要大于儿子结点存储数据(也可以是父亲结点数据都要小于儿子结点数据)的一种数据结构。堆只有两种即大堆和小堆,大堆就是父亲结点数据大于儿子结点数据,小堆则反之。
堆的性质:
-
堆中某个节点的值总是不大于或不小于其父节点的值;
-
堆总是一棵完全二叉树。

如图所示就是小根堆和大根堆的展示
2. 堆的代码及实现
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}HP;
void AdjustUp(HPDataType* a, int child);
void AdjustDown(int* a, int n, int parent);
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);
int HeapSize(HP* php);2.1 向下调整和向上调整
这里面我们这期主要就讲解两种方法:向下调整,向上调整这两种方法
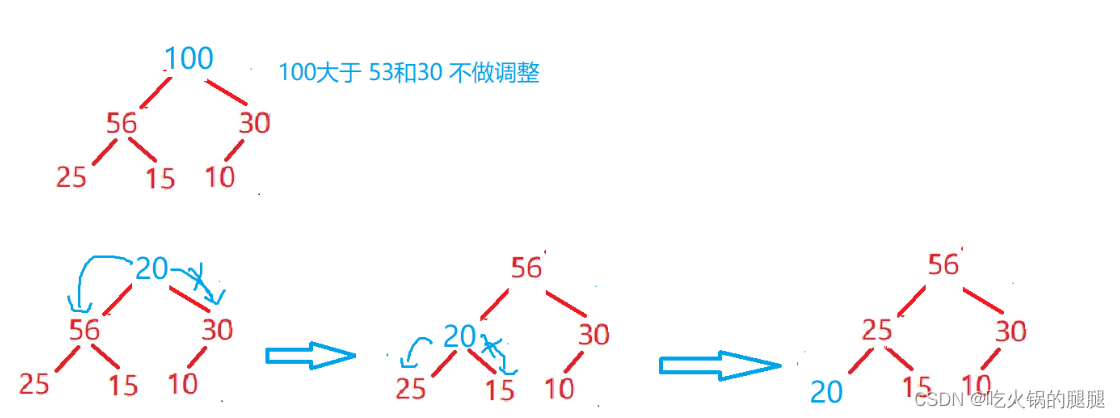
向下调整算法:作用就是通过从上到下的算法排序,将任意一个堆变成最小堆或者最大堆。
步骤:(此处以最小堆为例)
1、从根节点的左右孩子中选取一个较小值min
2、当前需要调整的数据与较小值min进行比较
- 大于min:和min进行交换,从交换后的位置继续执行第1步;
- 小于等于min:结束
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child<n)
{
if (a[child + 1] > a[child])
{
child++;
}
if(a[child]>a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}向上调整:图解思路
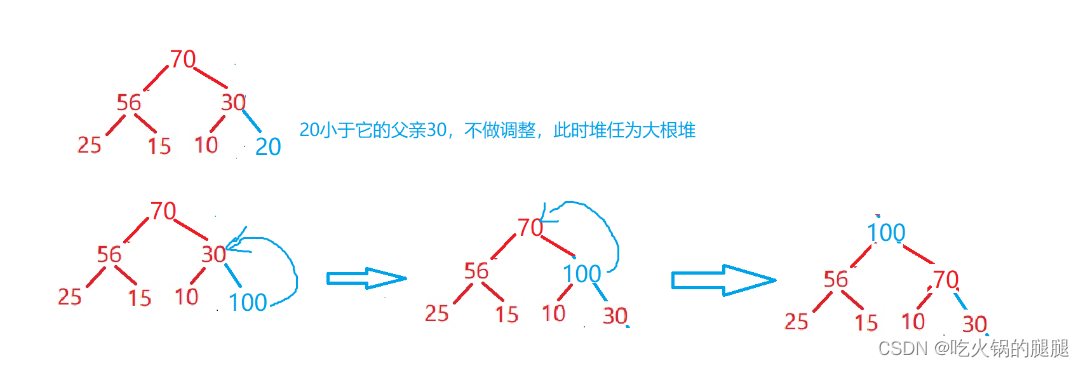
你每构建完一次小根堆,交换元素,你此时在数组上是不是把最小的元素放在末尾了,说明已经确定了,那我们就不需要动了,我们要动的就是数组那些没确定的元素,在这些里面去找一个最小的。那么这一步体现在堆上
举个例子,6,2.1.4 这么一组数我们第一次构建小根堆之后,1就跑到了堆顶,也就是跑到了数组首元素1,数组此时为1***,和最后一个元素交换,就成了** * 1,那么这个时候1就已经确定了,我们下来要做的是把**这三个构建出一个小根堆,这三个里最小的放在首元素
比方说是2** 1,我们交换2和这次没确定的数组最后一个元素,成了**21,此时2 和1已经确定了,我们再去剩下两个**去构建,去交换,最后得到 6 4 2 1
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child<n)
{
if (a[child + 1] > a[child])
{
child++;
}
if(a[child]>a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}代码实现:
#include"Heap.h"
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->size == php->capacity)
{
int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));
if (tmp == NULL)
{
perror("realloc fail");
return;
}
php->a = tmp;
php->capacity = newCapacity;
}
php->a[php->size] = x;
php->size++;
AdjustUp(php->a, php->size - 1);
}
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType* tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child<n)
{
if (a[child + 1] > a[child])
{
child++;
}
if(a[child]>a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void Heapop(HP* php)
{
assert(php);
assert(!HeapEmpty(php));
Swap(&php->a[0], &php->a[php->size - 1]);
php--;
AdjustDown(php->a, php->size, 0);
}
HPDataType HeapTop(HP* php)
{
assert(php);
assert(!HeapEmpty(php));
return php->a[0];
}
//
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
int HeapSize(HP* php)
{
assert(php);
return php->size;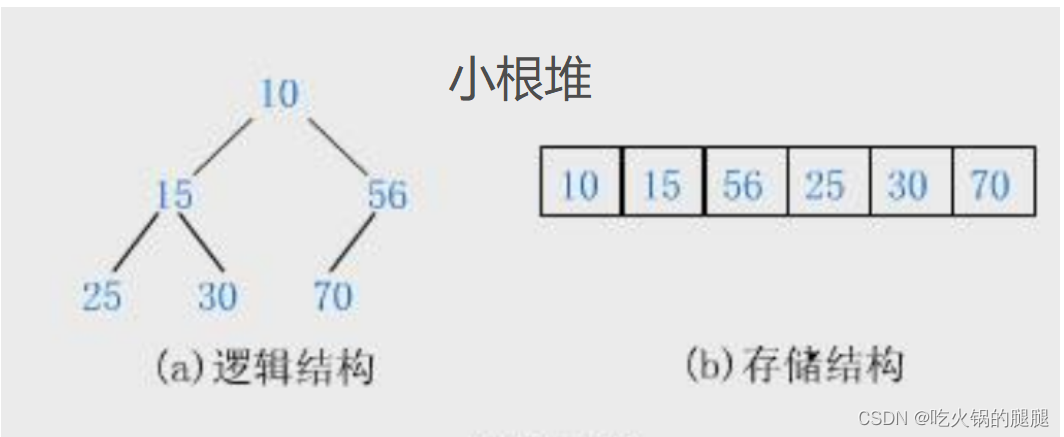



![[工业互联-23]:EtherCat从站 - EtherCAT协议栈与工作原理, 软硬件解决方案](https://img-blog.csdnimg.cn/img_convert/4f598be158a91d5620fb840e1900a897.png)
![LeetCode[394]字符串解码](https://img-blog.csdnimg.cn/a75939e3a17b4c9a965f188720012317.png)