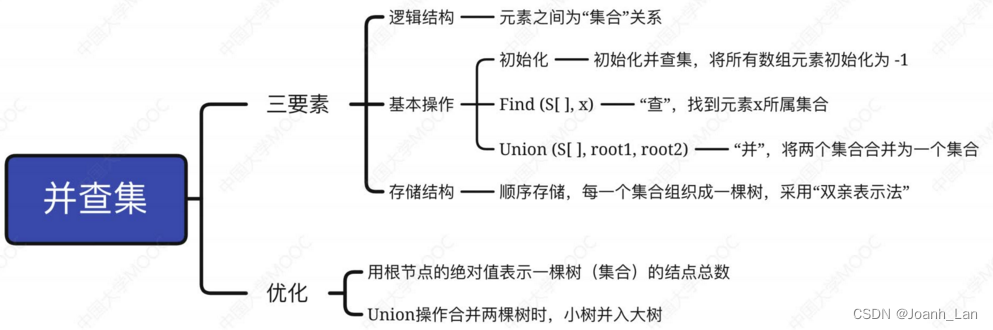
数据结构–并查集

逻辑结构―—“集合”

所有元素的全集s

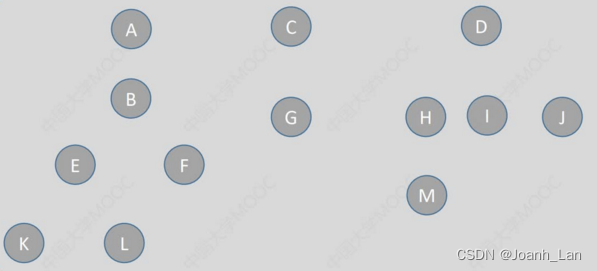
将各个元素划分为若干个互不相交的子集

用互不相交的树，表示多个“集合”

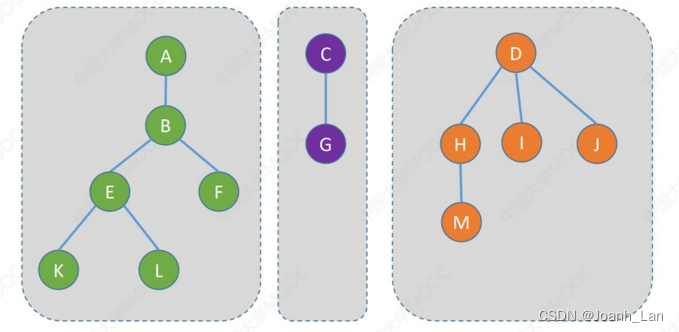
“并查集”的存储结构

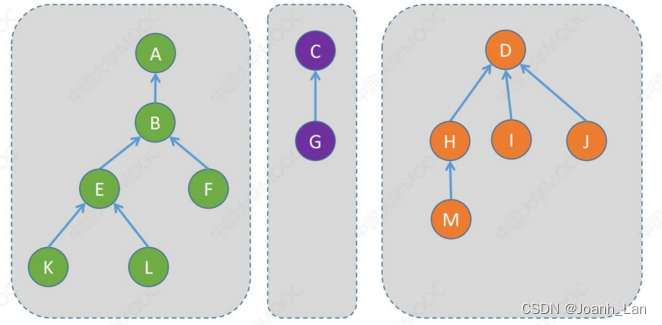
用一个数组S[ ]即可表示“集合”关系

‘并查集”的基本操作

集合的两个基本操作―—$“并”$和$“查”$
Find -—“查”操作:确定一个指定元素所属集合
Union --“并”操作:将两个不想交的集合合并为一个
注:并查集（Disjoint Set）是逻辑结构――集合的一种具体实现，只进行“并”和“查”两种基本操作

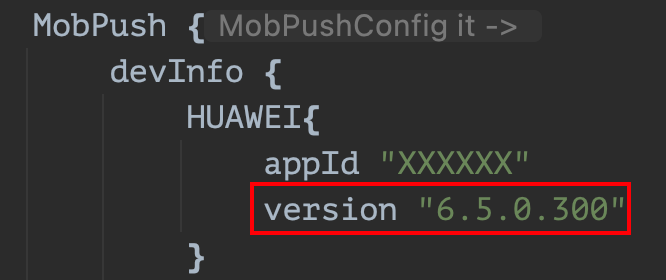
并查集”的代码实现―—初始化

#define SIZE 13
int UFSet[SIZE];

void Initial(int S[])
{
    for (int i = 0; i < SIZE; i++)
        S[i] = -1;
}

“并查集”的代码实现――并、查

int Find(int S[], int x)
{
    while (S[x] >= 0) //循环寻找x的根
        x = S[x];
    return x;
}
void Union(int S[], int Root1, int Root2)
{
    //要求Root1与Root2是不同的集合
    if (Root1 == Root2)
        return;
    //将根Root2连接到另一根Root1下面
    S[Root2] = Root1;
}

时间复杂度分析

Union 时间复杂度O(1)

找到 J 所属的集合

较好情况：

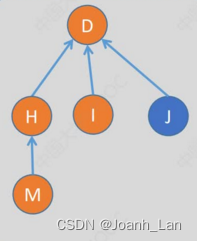
最坏情况：
高度 h = n

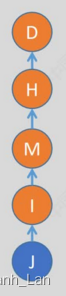
若结点数为n,Find $最坏时间复杂度为O(n)$

Union操作的优化

优化思路:在每次Union操作构建树的时候，尽可能让树不长高高
$①用根节点的绝对值表示树的结点总数$
$②Union操作，让小树合并到大树$

void Union(int S[], int Root1, int Root2)
{
    //要求Root1与Root2是不同的集合
    if (Root1 == Root2)
        return;
    if(S[Root2] > S [Root1]) //Root2结点数更少
    { 
        S[Root1] += S[Root2]; //累加结点总数
        S[Root2] = Root1; //小树合并到大树
    }
    else
    {
        S[Root2] += S[Root1]; //累加结点总数
        S[Root1] = Root2 ; //小树合并到大树
    }
}

Union操作优化后，Find操作最坏时间复杂度: $O(lo{g}_{2}n)$
该方法构造的树高不超过 $\lfloor {\log }_{2}n\rfloor +1$

知识点回顾与重要考点