【LeetCode热题100】打卡第34天：排序链表&乘积最大的子数组

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

排序链表

🔒题目

原题链接：148.排序链表

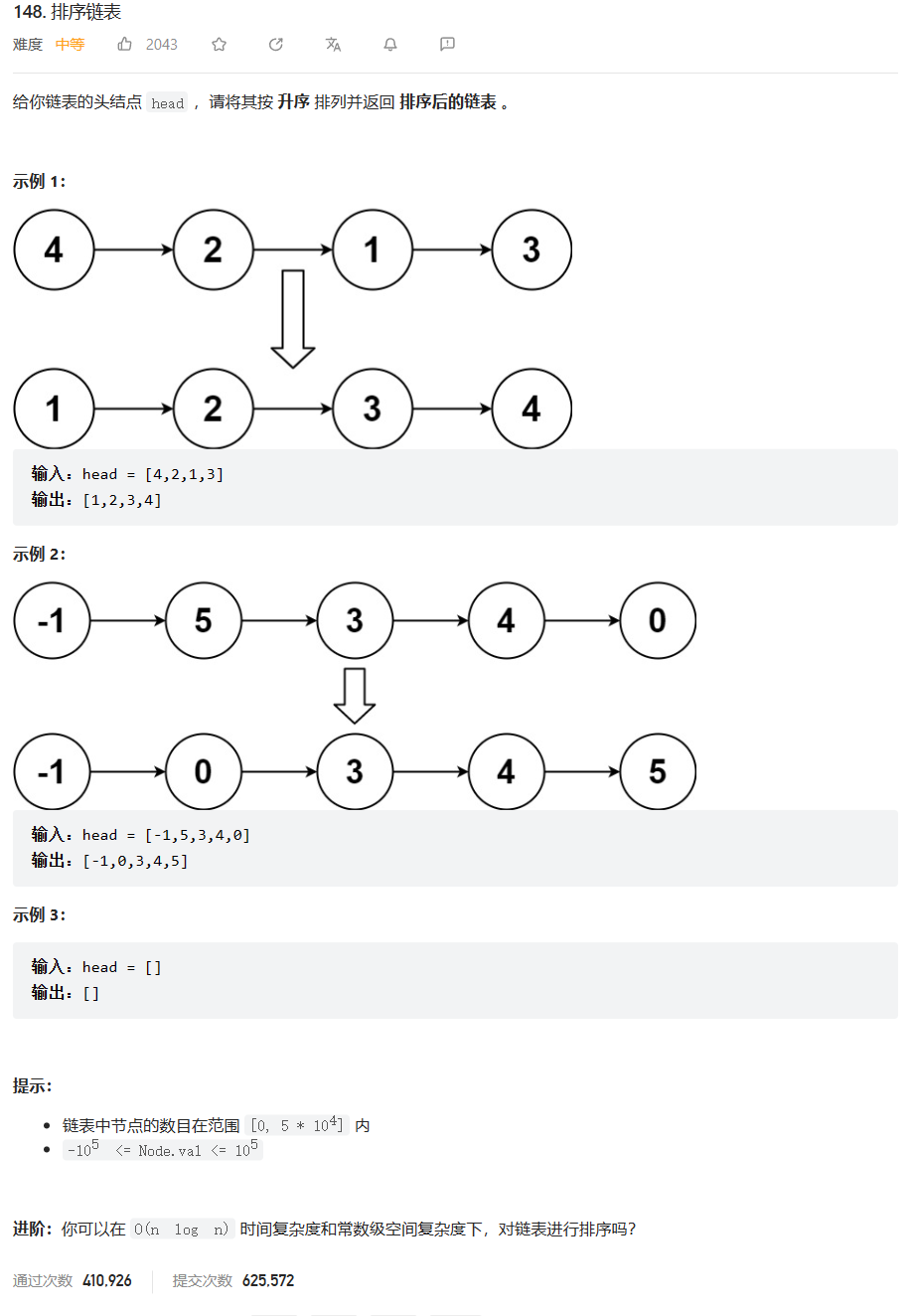
🔑题解

• 解法一：暴力枚举（超时，30个示例，过了29个，一个超时）

  public class Solution {
      // Node.val的最小值
      private int MIN_VALUE = -100000;
      
      public ListNode sortList(ListNode head) {
          ListNode newHead = new ListNode(MIN_VALUE);
          while (head != null) {
              ListNode i = newHead;
              // 从 newHead 中定位比 head 大的前一个节点
              while (i.next != null && i.next.val < head.val) {
                  i = i.next;
              }
              ListNode tempNode = new ListNode(head.val);
              if (i.next != null){
                  // 非尾节点
                  tempNode.next = i.next;
              }
              i.next = tempNode;
              head = head.next;
          }
          return newHead.next;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n^2)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为链表中元素的个数

• 解法二：归并排序

  这一题，要求时间复杂度是$O(nlogn)$，空间复杂度为$O(1)$基于这两点，很容易就联想到分治思想，而又结合排序就很容易想到归并排序，大家对于归并排序一定都熟记于心了吧(●ˇ∀ˇ●)，虽然很容易想到，但是换成链表我就发现实现起来是比较困难的，这里先复习一下数组版的归并排序吧（采用自底向上的归并排序）

  public class Test {
      public static void main(String[] args) {
          int[] arr = {4, 2, 1, 1, 5, -1, 1, 7, 5};
          // 归并排序
          mergeSort(arr, 0, arr.length - 1);
          // 输出结果
          System.out.println(Arrays.toString(arr));
      }
  
      private static void mergeSort(int[] arr, int l, int r) {
          if (l == r) {
              // 区间中只有一个元素，无需划分
              return;
          }
          // 计算区间中间索引（向下取整，往左逼近，mid在左）
          int mid = (r - l) / 2 + l;
          // 划分左侧子数组
          mergeSort(arr, l, mid);
          // 划分右侧子数组
          mergeSort(arr, mid + 1, r);
          // 合并区间
          merge(arr, l, mid, r);
      }
  
      private static void merge(int[] arr, int l, int mid, int r) {
          int[] temp = new int[arr.length];
          int i = l;
          int j = mid + 1;
          int k = 0;
          // 比较左右子树组中的元素，将较小值放入temp中（降序排序）
          while (i <= mid && j <= r) {
              if (arr[i] < arr[j]) {
                  temp[k++] = arr[i++];
              } else {
                  temp[k++] = arr[j++];
              }
          }
          // 左侧子数组还有剩余
          while (i <= mid) {
              temp[k++] = arr[i++];
          }
          // 右侧子数组还有剩余
          while (j <= r) {
              temp[k++] = arr[j++];
          }
          // 将 temp 拷贝到 arr 中
          for (int t = 0; t < k; t++) {
              arr[l+t] = temp[t];
          }
      }
  }
  

  以下代码参考自 K神

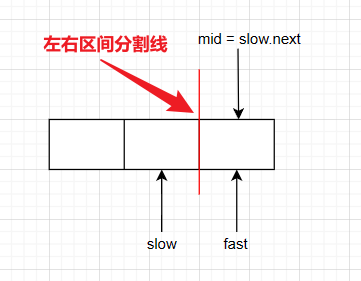
  链表实现归并排序的难点在于如何确定中间节点？这里采用一个比较巧妙的技巧，那就是使用快慢指针，在前面（LeetCode热题100打卡33天）我们判断链表是否有换，也是用到了快慢指针，这里同样的可以利用它来确定中间节点

  大致思路：快指针（fast）比慢指针（slow）多走一步，这样fast到达了链表尾部，slow就处在了中间节点的位置，这里需要注意的是已经有左侧边界了，还缺一个右侧边界，如果直接以slow为右侧边界，会导致有节点遗漏，这个在二分查找中就已经讨论过了，这里不再赘述，所以我们需要以 slow.next 为右侧边界，此外在我们选中了 slow.next 为右侧边界，我们还需要将 slow.next置为null，这样能够比较好的用来判断左侧链表是否遍历到头，否则还需要使用一个多余的变量来记录左侧边界值

  

  class Solution {
      public ListNode sortList(ListNode head) {
          return mergeSort(head);
      }
  
      private ListNode mergeSort(ListNode node) {
          if (node == null || node.next == null) {
              return node;
          }
          // 定位中间节点（向上取整，往右逼近，mid在右）
          ListNode fast = node.next;
          ListNode slow = node;
          while (fast != null && fast.next != null) {
              slow = slow.next;
              fast = fast.next.next;
          }
          ListNode mid = slow.next;
          slow.next = null;
          // 划分左侧子区间
          ListNode left = mergeSort(node);
          // 划分右侧子区间
          ListNode right = mergeSort(mid);
          // 合并区间
          return merge(left, right);
      }
  
      private ListNode merge(ListNode left, ListNode right) {
          ListNode res = new ListNode();
          // 比较左右子区间中的元素，将较小值放入temp中（降序排序）
          ListNode temp = res;
          while (left != null && right != null) {
              if (left.val < right.val) {
                  temp.next = left;
                  left = left.next;
              } else {
                  temp.next = right;
                  right = right.next;
              }
              temp = temp.next;
          }
          // 将剩余的一方添加到 temp 的尾部
          temp.next = left != null ? left : right;
          return res.next;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(nlogn)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数

  这种方法虽然能过，但是空间复杂度是$O(n)$，但这不符合进阶要求，进阶的要求是空间复杂度$O(1)$，所以递归实现归并是无法实现的，我们就需要使用迭代来实现归并排序：

  略……https://leetcode.cn/problems/sort-list/solution/javadi-gui-die-dai-shuang-zhong-jie-fa-luo-ji-qing/
  

  PS：迭代归并写起来好麻烦，不要折磨自己了，在我提交别人的代码测试后发现迭代归并虽然迭代归并空间复杂度为常数，但是内存消耗居然比递归归并还要多，耗时也要多，感兴趣的可以自行去LeetCode看别人迭代版的归并排序

• 解法三：快速排序

  同理，先来复习以下数组快排是如何实现的吧😄

  public class Test {
      public static void main(String[] args) {
          int[] arr = {4, 2, 1, 1, 5, -1, 1, 7, 5};
          quickSort(arr, 0, arr.length - 1);
          System.out.println(Arrays.toString(arr));
      }
  
      private static void quickSort(int[] arr, int l, int r) {
          if (l >= r) {
              // 区间中只有一个元素时或无元素时，无需继续划分区间
              return;
          }
          // 划分区间，并获取主元索引
          int pivot = partition(arr, l, r);
          // 划分左侧子区间
          quickSort(arr, l, pivot - 1);
          // 划分右侧子区间
          quickSort(arr, pivot + 1, r);
      }
  
      private static int partition(int[] arr, int l, int r) {
          // 选取主元（以区间末尾元素为主元）
          int pivot = arr[r];
          // 左侧区间右边界
          int i = l - 1;
          // 划分区间（左侧区间<主元，右侧区间>=主元）
          for (int j = l; j < r; j++) {
              // 将比主元小的元素放到 i+1 的左侧
              if (arr[j] < pivot) {
                  swap(arr, ++i, j);
              }
          }
          // 将主元放到分界点，然后返回主元索引
          swap(arr, i + 1, r);
          return i + 1;
      }
  
      private static void swap(int[] arr, int i, int j) {
          int temp = arr[j];
          arr[j] = arr[i];
          arr[i] = temp;
      }
  }
  

  class Solution {
      public static ListNode sortList(ListNode head) {
          return quickSort(head, null);
      }
  
      public static ListNode quickSort(ListNode head, ListNode end) {
          if (head == end || head.next == end) {
              // 区间中只有一个元素时或无元素时，无需继续划分区间
              return head;
          }
          // 划分区间，并获取主元节点
          ListNode pivot = partition(head, end);
          // 划分左侧子区间
          ListNode node = quickSort(pivot, head);
          // 划分右侧子区间
          head.next = quickSort(head.next, end);
          return node;
      }
  
      private static ListNode partition(ListNode head, ListNode end) {
          // 选头节点的值作为主元
          int pivot = head.val;
          // 左区间右边界
          ListNode i = head;
          // 右区间右边界
          ListNode j = head;
          // 遍历整个区间，并进行划分（左侧区间<主元，右侧区间>=主元）
          ListNode p = head.next; // 从第二个节点开始遍历
          while (p != end) {
              // 临时存储 p.next，防止链表断裂
              ListNode tempNode = p.next;
              // 将所有比主元小的元素都放到 i 的左侧，所有比主元大的元素都放到 j 的右侧
              if (p.val < pivot) {
                  // 头插
                  p.next = i;
                  i = p;
              } else {
                  // 尾插
                  j.next = p;
                  j = p;
              }
              p = tempNode;
          }
          j.next = end;
          return i;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(nlogn)$
  • 空间复杂度：$O(1)$

  其中 $n$ 为数组中元素的个数

乘积最大的子数组

🔒题目

原题链接：152.乘积最大的子数组

🔑题解

• 解法一：暴力枚举（能过）

  class Solution {
      public int maxProduct(int[] nums) {
          int maxProduct = Integer.MIN_VALUE;
          for (int i = 0; i < nums.length; i++) {
              int product = 1;
              for (int j = i; j < nums.length; j++) {
                  product *= nums[j];
                  maxProduct = Math.max(maxProduct, product);
              }
          }
          return maxProduct;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n^2)$
  • 空间复杂度：$O(1)$

• 解法二：动态规划

  解法一使用暴力枚举，每次都需要重新去计算左侧最大值，计算左侧最大值的过程其实是可以使用一个数组存储的，这样就不需要每次都去计算一遍左侧最大值，但是这样也带来了一个问题，那就是当前最大值，不一定是由左侧最大值更新过来的，有可能是由左侧最小值更新过来的，所以我们还需要使用一个数组去记录左侧最小值，总结起来，无非以下几种情况：

  max[i]：从第 0 个元素到 第 i 个元素（必须包含第i个元素），能够形成最大的连续乘积

  min[i]：从第 0 个元素到 第 i 个元素（必须包含第i个元素），能够形成最小的连续乘积

  1. 当前最大值由左侧最大值更新得到，max[i]=Math.max(nums[i],nums[i]*max[i-1])

  2. 当前最大值由左侧最小值更新得到，max[i]=Math.max(max[i],nums[i]*max[i-1])

     综合起来，就可以得到：max[i] = Math.max(max[i - 1] * nums[i], Math.max(nums[i], min[i - 1] * nums[i]))

     同理，我们可以得到：min[i] = Math.min(min[i - 1] * nums[i], Math.min(nums[i], max[i - 1] * nums[i]))

  最后我们只需要通过Math.max(ans, max[i])更新最大连续乘积即可

  class Solution {
      public int maxProduct(int[] nums) {
          int len = nums.length;
          int[] max = new int[len];
          max[0] = nums[0];
          int[] min = new int[len];
          min[0] = nums[0];
          // 更新计算出max数组和min数组
          for (int i = 1; i < len; ++i) {
              max[i] = Math.max(max[i - 1] * nums[i], Math.max(nums[i], min[i - 1] * nums[i]));
              min[i] = Math.min(min[i - 1] * nums[i], Math.min(nums[i], max[i - 1] * nums[i]));
          }
          // 更新计算出最大连续乘积
          int maxProduct = max[0];
          for (int i = 1; i < len; ++i) {
              maxProduct = Math.max(maxProduct, max[i]);
          }
          return maxProduct;
      }
  }
  

  我们可以发现在更新max和min数组时，其实也是可以顺便更新ans的，所以可以对上面代码进行简化

  class Solution {
      public int maxProduct(int[] nums) {
          int len = nums.length;
          int[] max = new int[len];
          max[0] = nums[0];
          int[] min = new int[len];
          min[0] = nums[0];
          int maxProduct = max[0];
          // 更新计算出max数组和min数组，同时更新ans
          for (int i = 1; i < len; ++i) {
              max[i] = Math.max(max[i - 1] * nums[i], Math.max(nums[i], min[i - 1] * nums[i]));
              min[i] = Math.min(min[i - 1] * nums[i], Math.min(nums[i], max[i - 1] * nums[i]));
              maxProduct = Math.max(maxProduct, max[i]);
          }
          return maxProduct;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数

  代码优化：空间优化

  我们发现每次更新，其实max和min后面的元素都没有用到，我们只用到了上一次的状态，这就我们的状态方程只有上一个状态有关，这就说明我们可以仅使用有关变量去记录上一个状态

  class Solution {
      public int maxProduct(int[] nums) {
          int len = nums.length;
          int max = nums[0];
          int min = nums[0];
          int maxProduct = nums[0];
          for (int i = 1; i < len; ++i) {
              int preMax = max;
              int preMin = min;
              max = Math.max(preMax * nums[i], Math.max(nums[i], preMin * nums[i]));
              min = Math.min(preMin * nums[i], Math.min(nums[i], preMax * nums[i]));
              maxProduct = Math.max(maxProduct, max);
          }
          return maxProduct;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(1)$

  其中 $n$ 为数组中元素的个数