代码展示：

class Solution {
    public int uniquePaths(int m, int n) {
        //定义dp数组
        //二维数组多增加一行一列，方便对数组进行初始化
        int[][]dp=new int[m+1][n+1];
        //初始化
        dp[0][1]=1;
        //填充数组
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m][n];
    }
}

        1.状态表示

                我们采用从后往前的方式推导，我们现在想要求dp[i][j]的值，也就是到i，j位置的不同路径条数，由于机器人只能向下和向右移动，所以我们可以从两个地方到达i，j的位置

        （1）.我们可以在i-1，j的位置向下移动到达i，j的位置

        （2）.我们可以在i，j-1的位置向右移动到达i，j的位置

        而第一种情况，我们首先要到达i-1，j的位置，而到达i-1，j的位置有dp[i-1][j]种不同的路径，第二种情况，我们首先要到达i，j-1的位置，而到达i，j-1的位置有dp[i][j-1]种不同的路径，所以总共的路径有dp[i-1][j]+dp[i][j-1]

        2.状态转移方程

                通过以上的分析我们也得到了状态转移方程，dp[i][j]=dp[i-1][j]+dp[i][j-1]

        3.定义dp数组进行初始化

                我们可以在创建dp数组时添加辅助结点，这样可以使我们的初始化更加的简单。由于该题中的dp数组是二维数组，所以我们可以将dp数组扩充一行一列

        如图是添加辅助结点前后的初始化对比：

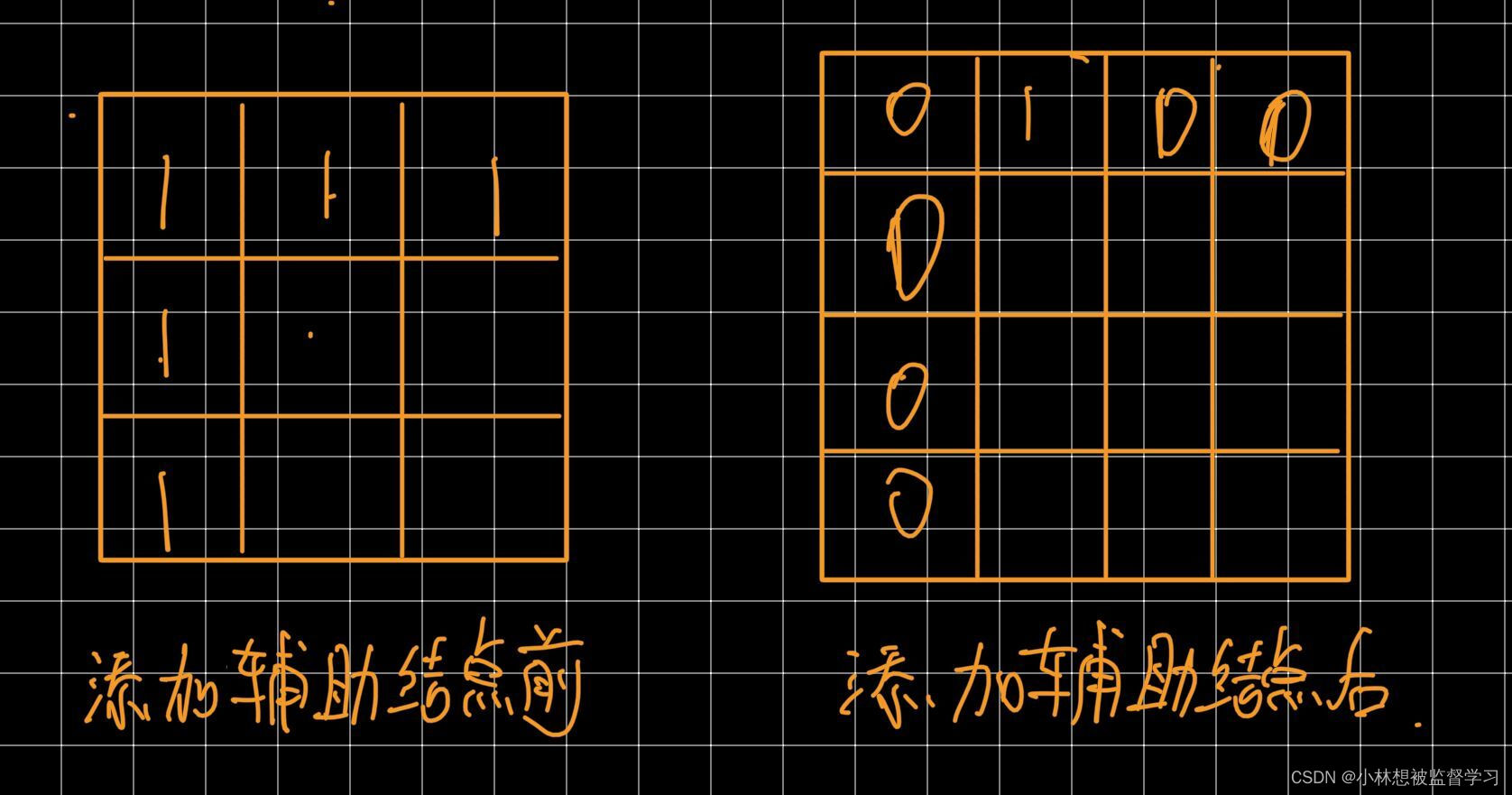
         要是不添加辅助结点也可以将数组的第0行和第0列都初始化为1，在该题中辅助结点的意义不大，但在其他的很多题中，辅助结点可以让你的初始化变得格外简单

        4.根据状态转移方程填充数组

        5.返回值

通过以上步骤便可得出答案