一.双指针
主要分为俩种类型:
1.左右指针:双指针指向开头,以一定标准移动或交换,对区域进行划分,或找到特殊点的位置
(如:快慢指针判断有无环,移动零)
2.对撞指针:在有序或者特殊数组中,可以利用单调性,双指针分别指向开头和结尾,利用单调性,对数组中的元素进行排除,从而进行指针移动。
(如:找和为目标值的俩个数)
第一种类型题1
移动零
已解答
简单
相关标签
相关企业
提示
给定一个数组
nums,编写一个函数将所有0移动到数组的末尾,同时保持非零元素的相对顺序。请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums =[0,1,0,3,12]输出:[1,3,12,0,0]示例 2:
输入: nums =[0]输出:[0]提示:
1 <= nums.length <= 104-231 <= nums[i] <= 231 - 1进阶:你能尽量减少完成的操作次数吗?
题意讲解:就是将数组中的零移动到最后,并且不能复制数组。
算法原理:就是下面代码的逻辑
int n=nums.size();
int right=0;
int left=-1;
while(right<n)
{
if(nums[right]==0)
{
right++;
}
else if(nums[right]!=0)
{
left++;
swap(nums[left],nums[right]);
right++;
}
}

right遇到0元素++,遇到非零元素,先让left++,再交换元素,再让right++。主要目的就是划分成下面几个区域:
[0,left] 是非零元素,[left+1,right] 0元素,[right,n-1]待处理元素。
当right移动到中点就完成了。(快排也是这样的思路)
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int n=nums.size();
int right=0;
int left=-1;
while(right<n)
{
if(nums[right]==0)
{
right++;
}
else if(nums[right]!=0)
{
left++;
swap(nums[left],nums[right]);
right++;
}
}
}
};2.第二种类型
179. 查找总价格为目标值的两个商品
已解答
简单
相关标签
相关企业
购物车内的商品价格按照升序记录于数组
price。请在购物车中找到两个商品的价格总和刚好是target。若存在多种情况,返回任一结果即可。示例 1:
输入:price = [3, 9, 12, 15], target = 18 输出:[3,15] 或者 [15,3]示例 2:
输入:price = [8, 21, 27, 34, 52, 66], target = 61 输出:[27,34] 或者 [34,27]
算法原理:
1.对数组进行排序,再让俩个指针(left,right)指向开头和结尾的位置
2.利用单调性:
当a[left]+a[right]大于target,说明右边的数和最小的数在一起都大了,右边这个数排除储数组,不再考虑。即right++。
当a[left]+a[right]小于target,说明左边的数和最大的数在一起都小了,左边这个数排除储数组,不再考虑。即left++。
代码如下:
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
//利用单调性
int n=price.size();
int left=0;
int right=n-1;
vector<int> ret;
while(right>left)
{
if(price[left]+price[right]==target)
{
ret.push_back(price[left]);
ret.push_back(price[right]);
break;
}
else if(price[left]+price[right]>target)
{
right--;
}
else
{
left++;
}
}
return ret;
}
};二.滑动窗口
特点:求一段连续的区间,需要利用单调性,左右指针不回退。
模板:

更新结果的位置不确定。
长度最小的子数组
已解答
中等
相关标签
相关企业
给定一个含有
n个正整数的数组和一个正整数target。找出该数组中满足其总和大于等于
target的长度最小的 子数组[numsl, numsl+1, ..., numsr-1, numsr],并返回其长度。如果不存在符合条件的子数组,返回0。示例 1:
输入:target = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组[4,3]是该条件下的长度最小的子数组。示例 2:
输入:target = 4, nums = [1,4,4] 输出:1示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1] 输出:0提示:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 104
代码:
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int n=nums.size();
int left=0;
int right=0;
int sum=0;
int len=INT_MAX;
while(right<n)
{
sum+=nums[right];//进窗口
while(sum>=target)//判断
{
len=min(-left+right+1,len);//更新
if(len==1)
{
return 1;
}
sum-=nums[left];
left++;//出窗口
}
right++;
}
return len==INT_MAX?0:len;
}
};三.二分法
特点:数组具有二段性。
类型1:找一个值(在有序数组中二分查找一个值)
类型2:找左右区间。模板如下:

看题目快速理解。
在排序数组中查找元素的第一个和最后一个位置
已解答
中等
相关标签
相关企业
给你一个按照非递减顺序排列的整数数组
nums,和一个目标值target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值
target,返回[-1, -1]。你必须设计并实现时间复杂度为
O(log n)的算法解决此问题。示例 1:
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4]示例 2:
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]示例 3:
输入:nums = [], target = 0 输出:[-1,-1]提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一个非递减数组-109 <= target <= 109
就是找等于目标值的左右区间。
我们以[5,6,7,8,8,8,8,9,9,10,10],taget=8为例子
可以划分成下面区域:

我们需要找到第2端的起始位置,也就是目标值的左区间。

我们需要找到第1端的终结位置,也就是目标值的右区间。
可以看到左右区间值将数组分成2端,这时具有二段性可以用二分法。
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
vector<int>ret(2,-1);
if(nums.size()==0)
{
return ret;
}
int n=nums.size();
int begin;
int end;
int left=0;
int right=n-1;
//1.找左区间
while(left<right)
{
int middle=left+(right-left)/2;
if(nums[middle]<target)
{
left=middle+1;
}
else
{
right=middle;
}
}
if(nums[left]!=target)
{
return ret;
}
ret[0]=(left);
right=n-1;
//2.找右边区间
while(left<right)
{
int middle=left+(right-left+1)/2;
if(nums[middle]<=target)
{
left=middle;
}
else
{
right=middle-1;
}
}
ret[1]=(left);
return ret;
}
};要注意几个点
1.循环条件为left<right,写成left<=right会死循环,同时left==right,就是最终值,不用再判断。
2.middle=left+(right-left)/2是在偶数个数取中间前面的一个。midddle=left+(right-left+1)/2是在偶数个数中取后面的一个。该怎么区分:
当right=middle-1时让middle=left+(right-left+1)/2。即有-1,再+1
原因:如找左区间时, int middle=left+(right-left)/2;
if(nums[middle]<target)
{
left=middle+1;
}
else
{
right=middle;
}假设:当区间不断缩小为俩个值,区间为7,8。left指向7,right指向8。
不加1时,middle指向7,小于8,left=middle+1,left==right找到正确值。
加1时,middle指向8,right=middle,还是指向8.right不动了,死循环。
因此对于不同的情况要采用不同的取法。
四.前缀和
本质也就是动态规划的一种情况。常用于求一段满足特定条件的连续区间,可能会用到哈希表,找一段区间常用的是终点的dp-起点的dp。
1.一维前缀和
前缀和
- 题目
- 题解(49)
- 讨论(22)
- 排行
简单 通过率:27.59% 时间限制:1秒 空间限制:128M
校招时部分企业笔试将禁止编程题跳出页面,为提前适应,练习时请使用在线自测,而非本地IDE。
描述
给定一个长度为n的数组a1,a2,....ana1,a2,....an.
接下来有q次查询, 每次查询有两个参数l, r.
对于每个询问, 请输出al+al+1+....+aral+al+1+....+ar
输入描述:
第一行包含两个整数n和q.
第二行包含n个整数, 表示a1,a2,....ana1,a2,....an.
接下来q行,每行包含两个整数 l和r.
1≤n,q≤1051≤n,q≤105
−109≤a[i]≤109−109≤a[i]≤109
1≤l≤r≤n1≤l≤r≤n输出描述:
输出q行,每行代表一次查询的结果.
示例
输入:
3 2
1 2 4
1 2
13输出:
3
6
思路是建立一个dp表存入从起点到i位置的所有前缀和。
dp=dp[i-1]+nums[i];
要求l到r位置的前缀和就用dp[r]-dp[l-1]就行。
#include <iostream>
#include<vector>
using namespace std;
int main() {
int n;
int q;
cin>>n;
cin>>q;
vector<int> v(n+1,0);
vector<long long> dp(n+1,0);
for(int i=1;i<=n;i++)
{
cin>>v[i];
}
for(int i=1;i<=n;i++)
{
dp[i]=v[i]+dp[i-1];
}
for(int i=0;i<q;i++)
{
int l,r;
cin>>l>>r;
cout<<dp[r]-dp[l-1]<<endl;
}
}
// 64 位输出请用 printf("%lld")类型二:二维前缀和:
给你一个 n 行 m 列的矩阵 A ,下标从1开始。
接下来有 q 次查询,每次查询输入 4 个参数 x1, y1, x2, y2
请输出以(x1, y1) 为左上角, (x2, y2) 为右下角的子矩阵的和
第一行包含三个整数n, m, q.接下来n行,每行m个整数,代表矩阵的元素
接下来q行,每行4个整数x1, y1, x2, y2,分别代表这次查询的参数
输出描述:
输出q行,每行表示查询结果。
示例1
输入:
3 4 3
1 2 3 4
3 2 1 0
1 5 7 8
1 1 2 2
1 1 3 3
1 2 3 4
复制
输出:
8
25
32
思路:记录创建一个二维数组dp,dp[i][j]表示从起点到i,j位置的矩阵值。
dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+nums[i][j];
求x1,y1到x2,y2的值为
dp[x2][y2]-dp[x2][y1-1]-dp[x1-1][y2]+dp[x1-1][y1-1];
代码:
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n,m,q;
cin>>n>>m>>q;
vector<vector<int>>nums(n+1,vector<int>(m+1));
vector<vector<long long>> dp(n+1,vector<long long>(m+1));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>nums[i][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]+nums[i][j];
}
}
int x1,x2,y1,y2;
while(q--)
{
cin>>x1>>y1>>x2>>y2;
cout<<dp[x2][y2]-dp[x2][y1-1]-dp[x1-1][y2]+dp[x1-1][y1-1]<<endl;
}
}
// 64 位输出请用 printf("%lld")
要满足(dp[i]-d[j-1])%k==0,则dp[j-1]要和dp[i]具有相同的余数。即dp[j-1]=(dp[i]%p+p)%p。
和可被 K 整除的子数组
已解答
中等
相关标签
相关企业
给定一个整数数组
nums和一个整数k,返回其中元素之和可被k整除的非空 子数组 的数目。子数组 是数组中 连续 的部分。
示例 1:
输入:nums = [4,5,0,-2,-3,1], k = 5 输出:7 解释: 有 7 个子数组满足其元素之和可被 k = 5 整除: [4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]示例 2:
输入: nums = [5], k = 9 输出: 0
class Solution {
public:
int subarraysDivByK(vector<int>& nums, int k) {
unordered_map<int,int> hash;
hash[0]=1;//0这个数的余数
int n=nums.size();
int sum=0,ret=0;
for(auto &x:nums)
{
sum+=x;
int find=(sum%k+k)%k;
if(hash.count(find))
{
ret+=hash[find];
}
hash[find]++;
}
return ret;
}
};五.位运算

给你一个整数数组
nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。
示例 1:
输入:nums = [1,2,1,3,2,5] 输出:[3,5] 解释:[5, 3] 也是有效的答案。示例 2:
输入:nums = [-1,0] 输出:[-1,0]示例 3:
输入:nums = [0,1] 输出:[1,0]提示:
2 <= nums.length <= 3 * 104-231 <= nums[i] <= 231 - 1- 除两个只出现一次的整数外,
nums中的其他数字都出现两次
五.模拟
数青蛙
已解答
中等
相关标签
相关企业
提示
给你一个字符串
croakOfFrogs,它表示不同青蛙发出的蛙鸣声(字符串"croak")的组合。由于同一时间可以有多只青蛙呱呱作响,所以croakOfFrogs中会混合多个“croak”。请你返回模拟字符串中所有蛙鸣所需不同青蛙的最少数目。
要想发出蛙鸣 "croak",青蛙必须 依序 输出
‘c’, ’r’, ’o’, ’a’, ’k’这 5 个字母。如果没有输出全部五个字母,那么它就不会发出声音。如果字符串croakOfFrogs不是由若干有效的 "croak" 字符混合而成,请返回-1。示例 1:
输入:croakOfFrogs = "croakcroak" 输出:1 解释:一只青蛙 “呱呱” 两次示例 2:
输入:croakOfFrogs = "crcoakroak" 输出:2 解释:最少需要两只青蛙,“呱呱” 声用黑体标注 第一只青蛙 "crcoakroak" 第二只青蛙 "crcoakroak"示例 3:
输入:croakOfFrogs = "croakcrook" 输出:-1 解释:给出的字符串不是 "croak" 的有效组合

class Solution {
public:
int minNumberOfFrogs(string croakOfFrogs) {
int hash[5] = {0};
string s = "croak";
unordered_map <char,int> index;
for(int i=0;i<5;i++)
{
index[s[i]]=i;
}
for (int i = 0; i < croakOfFrogs.size(); i++) {
char temp = croakOfFrogs[i];
if (temp == 'c') {
if (hash[4] > 0) {
hash[4]--;
hash[0]++;
} else {
hash[0]++;
}
} else {
int cur = index[temp];
int pre = cur - 1;
if (hash[pre] > 0) {
hash[pre]--;
hash[cur]++;
} else {
return -1;
}
}
}
for(int i=0;i<4;i++)
{
if(hash[i]>0)
{
return -1;
}
}
return hash[4];
}
};六.分治
类型一:三指针
用三个指针,left,i,right,[0,left]小于特定值,[left+1,i]等于特定值,[i+1,right]大于特定值。把区域分成三份,常用于重复元素多的快排,快速选择算法。
数组中的第K个最大元素
已解答
中等
相关标签
相关企业
给定整数数组
nums和整数k,请返回数组中第k个最大的元素。请注意,你需要找的是数组排序后的第
k个最大的元素,而不是第k个不同的元素。你必须设计并实现时间复杂度为
O(n)的算法解决此问题。示例 1:
输入:[3,2,1,5,6,4],k = 2 输出: 5示例 2:
输入:[3,2,3,1,2,4,5,5,6],k = 4 输出: 4提示:
1 <= k <= nums.length <= 105-104 <= nums[i] <= 104

class Solution {
int dfs(int begin,int end,vector<int>&nums,int k)
{
if(begin>end)
{
return -1;
}
int left=begin-1;
int right=end+1;
int value=nums[(rand()%(end-begin+1))+begin];
for(int cur=left+1;cur<right;)
{
if(nums[cur]>value)
{
swap(nums[--right],nums[cur]);
}
else if(nums[cur]==value)
{
cur++;
}
else
{
swap(nums[++left],nums[cur++]);
}
}
int len1=end-right+1;
int len2=end-left;
if(len1>=k)
{
return dfs(right,end,nums,k);
}
else if(len2>=k)
{
return value;
}
else
{
return dfs(begin,left,nums,k-len2);
}
}
public:
int findKthLargest(vector<int>& nums, int k) {
return dfs(0,nums.size()-1,nums,k);
}
};类型二:归并排序
交易逆序对的总数
已解答
困难
相关标签
相关企业
在股票交易中,如果前一天的股价高于后一天的股价,则可以认为存在一个「交易逆序对」。请设计一个程序,输入一段时间内的股票交易记录
record,返回其中存在的「交易逆序对」总数。示例 1:
输入:record = [9, 7, 5, 4, 6] 输出:8 解释:交易中的逆序对为 (9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。
找出左区间和右区间的逆序对,并排序,在找左右区间结合的逆序对。
class Solution {
vector<int>ret;
int result=0;
void dfs(vector<int>& nums,int begin,int end)
{
if(begin>=end)
{
return;
}
int middle=begin+(end-begin)/2;
dfs(nums,begin,middle);
dfs(nums,middle+1,end);
int begin1=begin;
int end1=middle;
int begin2=middle+1;
int end2=end;
int i=0;
while(begin1<=end1&&begin2<=end2)
{
if(nums[begin1]<=nums[begin2])
{
ret[i++]=nums[begin1++];
}
else
{
result+=middle-begin1+1;
ret[i++]=nums[begin2++];
}
}
while(begin1<=end1)
{
ret[i++]=nums[begin1++];
}
while(begin2<=end2)
{
ret[i++]=nums[begin2++];
}
for(int i=begin;i<=end;i++)
{
nums[i]=ret[i-begin];
}
}
public:
int reversePairs(vector<int>& record) {
ret.resize(record.size());
dfs(record,0,record.size()-1);
return result;
}
};七.链表

 八.哈希表
八.哈希表
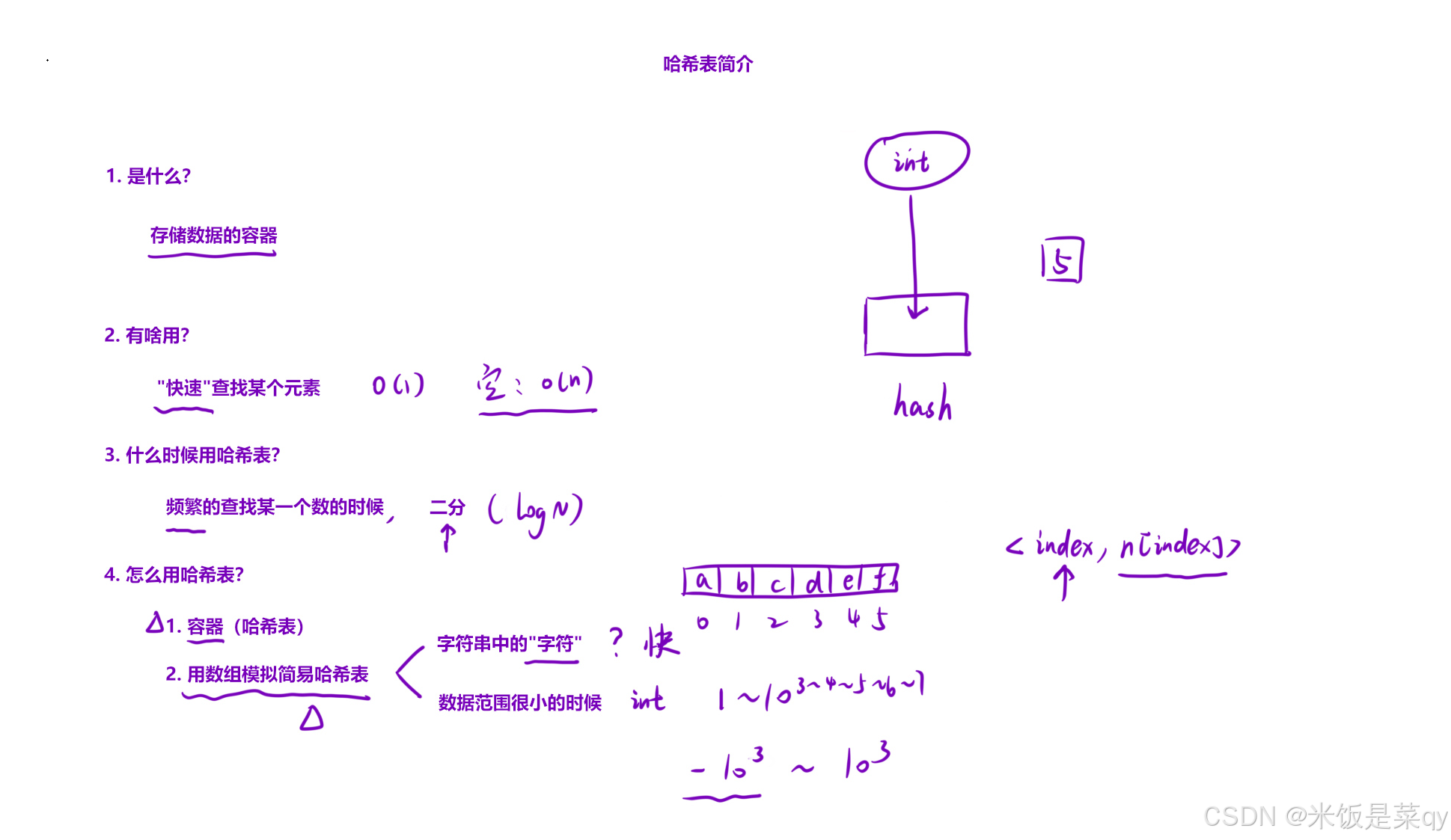
字母异位词分组
已解答
中等
相关标签
相关企业
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例 1:
输入: strs =["eat", "tea", "tan", "ate", "nat", "bat"]输出: [["bat"],["nat","tan"],["ate","eat","tea"]]示例 2:
输入: strs =[""]输出: [[""]]示例 3:
输入: strs =["a"]输出: [["a"]]
互为字⺟异位词的单词有⼀个特点:将它们「排序」之后,两个单词应该是「完全相同」的。 所以,我们可以利⽤这个特性,将单词按照字典序排序,如果排序后的单词相同的话,就划分到同⼀ 组中。排序后的string 作key,vector<string>作value
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
unordered_map<string,vector<string>> hash;
vector<vector<string>> ret;
for(auto e:strs)
{
string cur=e;
sort(e.begin(),e.end());
hash[e].push_back(cur);
}
for(auto e:hash)
{
ret.push_back(e.second);
}
return ret;
}
};九.字符串
最长回文子串
已解答
中等
相关标签
相关企业
提示
给你一个字符串
s,找到s中最长的 回文 子串。示例 1:
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。示例 2:
输入:s = "cbbd" 输出:"bb
特点:回文串从中心扩展俩边相同。主要的是有俩种扩展情况如:121 1221。
class Solution {
int len=1;
int start;
void findlen(int left,int right,string&s)
{
while(left>=0&&right<s.size()&&s[left]==s[right])
{
left--;
right++;
}
if((right-left-1)>len)
{
start=left+1;
len=right-left-1;
}
}
public:
string longestPalindrome(string s) {
start=s.size()-1;
if(s.size()==1)
{
return s;
}
for(int i=0;i<s.size();i++)
{
int left=i;
int right=i+1;
findlen(i,i+1,s);
findlen(i-1,i+1,s);
}
return s.substr(start,len);
}
};高精度加法:
二进制求和
已解答
简单
相关标签
相关企业
给你两个二进制字符串
a和b,以二进制字符串的形式返回它们的和。示例 1:
输入:a = "11", b = "1" 输出:"100"示例 2:
输入:a = "1010", b = "1011" 输出:"10101"
class Solution {
public:
string addBinary(string a, string b) {
int size1=a.size();
int size2=b.size();
int size=size1>size2?size1+1:size2+1;
string ret(size,'0');
int carry=0;
for(int i=0;i<a.size()||i<b.size()||carry;i++)
{
int char1=(i<a.size())?(a[a.size()-1-i]-'0'):0;
int char2=i<b.size()?b[b.size()-1-i]-'0':0;
int sum=char1+char2+carry;
ret[size-1-i]=sum%2+'0';
carry=sum/2;
}
if(ret[0]=='0')
{
ret.erase(0,1);
}
return ret;
}
};高进度乘法
字符串相乘
已解答
中等
相关标签
相关企业
给定两个以字符串形式表示的非负整数
num1和num2,返回num1和num2的乘积,它们的乘积也表示为字符串形式。注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
计算两数相乘的时候,先不考虑进位,等到所有结果计算完毕之后,再去考虑进位 。
class Solution {
public:
string multiply(string num1, string num2) {
if(num1=="0"||num2=="0")
{
return "0";
}
reverse(num1.begin(),num1.end());
reverse(num2.begin(),num2.end());
string ret="";
int n=num1.size();
int m=num2.size();
vector<int> arr (m+n-1);
for(int i=0;i<m;i++)
{
int t1=num2[i]-'0';
for(int j=0;j<n;j++)
{
int t2=num1[j]-'0';
arr[i+j]+=(t1*t2);
}
}
int t=0;
int i=0;
while(i<m+n-1||t>0)
{
if(i<m+n-1)
{
t+=arr[i];
}
char cur=(t%10)+'0';
ret+=cur;
i++;
t=t/10;
}
reverse(ret.begin(), ret.end());
return ret;
}
};十.栈
需要存储元素,元素后进先出。常用俩个栈,存不同类型的数据,再以特定规律用栈顶元素结合。
基本计算器 II
已解答
中等
相关标签
相关企业
给你一个字符串表达式
s,请你实现一个基本计算器来计算并返回它的值。整数除法仅保留整数部分。
你可以假设给定的表达式总是有效的。所有中间结果将在
[-231, 231 - 1]的范围内。注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如
eval()

class Solution {
public:
int calculate(string s) {
vector<int> st; // ⽤数组来模拟栈结构
int i = 0, n = s.size();
char op = '+';
while (i < n) {
if (s[i] == ' ')
i++;
else if (s[i] >= '0' && s[i] <= '9')
{
// 先把这个数字给提取出来
int tmp = 0;
while (i < n && s[i] >= '0' && s[i] <= '9')
tmp = tmp * 10 + (s[i++] - '0');
if (op == '+')
st.push_back(tmp);
else if (op == '-')
st.push_back(-tmp);
else if (op == '*')
st.back() *= tmp;
else
st.back() /= tmp;
}
else {
op = s[i];
i++;
}
}
int ret = 0;
for (auto x : st)
ret += x;
return ret;
}
};字符串解码
已解答
中等
相关标签
相关企业
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为:
k[encoded_string],表示其中方括号内部的encoded_string正好重复k次。注意k保证为正整数。你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数
k,例如不会出现像3a或2[4]的输入

class Solution {
public:
string decodeString(string s) {
vector<int> nums;
vector<string> ss(1,"");
int i=0;
int n=s.size();
while(i<n)
{
if(s[i]<='9'&&s[i]>='0')
{
string tmp="";
while(i<n&&s[i]<='9'&&s[i]>='0') tmp+=s[i++];
nums.push_back((stoi(tmp)));
}
else if(s[i]=='[')
{
string tmp="";
i++;
while(i<n&&s[i]>='a'&&s[i]<='z') tmp+=s[i++];
ss.push_back(tmp);
}
else if(s[i]==']')
{
i++;
int count=nums.back();
nums.pop_back();
string tmp=ss.back();
ss.pop_back();
string result="";
while(count--)
{
result+=tmp;
}
ss[ss.size()-1]+=result;
}
else
{
string tmp="";
while(i<n&&s[i]>='a'&&s[i]<='z') tmp+=s[i++];
ss[ss.size()-1]+=tmp;
}
}
return ss[0];
}
};十一.队列+宽度搜索
N 叉树的层序遍历
已解答
中等
相关标签
相关企业
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> ret;
queue<Node*> q;
if(root==nullptr)
{
return ret;
}
q.push(root);
int count=q.size();
while(q.size())
{
vector<int> tmp ;
while(count--)
{
Node* head=q.front();
vector<Node*> ch=head->children;
if(ch.size()>0)
{
for(auto &e:ch)
{
q.push(e);
}
}
tmp.push_back(head->val);
q.pop();
}
ret.push_back(tmp);
count=q.size();
}
return ret;
}
};二叉树最大宽度
已解答
中等
相关标签
相关企业
给你一棵二叉树的根节点
root,返回树的 最大宽度 。树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的
null节点,这些null节点也计入长度。题目数据保证答案将会在 32 位 带符号整数范围内

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
queue<pair<TreeNode*,long long>> q;
q.push(make_pair(root,1));
long long m=1;
int count=1;
while(q.size())
{
long long k=q.back().second-q.front().second+1;
m=max(m,k);
while(count--)
{
TreeNode* head=q.front().first;
int i=q.front().second;
TreeNode* left_ch=head->left;
if(left_ch!=nullptr)
{
q.push(make_pair(left_ch,(long long)2*i));
}
TreeNode* right_ch=head->right;
if(right_ch!=nullptr)
{
q.push(make_pair(right_ch,(long long)2*i+1));
}
q.pop();
}
count=q.size();
}
return m;
}
};十二.堆
默认是大堆,要实现自定义排序,要自己实现比较器
前K个高频单词
已解答
中等
相关标签
相关企业
给定一个单词列表
words和一个整数k,返回前k个出现次数最多的单词。返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率, 按字典顺序 排序。
class Solution {
public:
class cmp
{
public:
bool operator()(const pair<string,int> &p1,const pair<string,int> &p2)
{
if(p1.second!=p2.second)
{
return p1.second>p2.second;
}
return p1.first<p2.first;
}
};
vector<string> topKFrequent(vector<string>& words, int k) {
unordered_map<string,int> hash;
priority_queue<pair<string ,int>, vector<pair<string ,int>>, cmp>heap;
for(auto &e:words)
{
hash[e]++;
}
for(auto &e:hash)
{
heap.push(e);
if(heap.size()>k)
{
heap.pop();
}
}
vector<string> ret(k);
for(int i = k - 1; i >= 0; i--)
{
ret[i] = heap.top().first;
heap.pop();
}
return ret;
}
};十三.bfs
fooldfill算法
岛屿的最大面积
已解答
中等
相关标签
相关企业
给你一个大小为
m x n的二进制矩阵grid。岛屿 是由一些相邻的
1(代表土地) 构成的组合,这里的「相邻」要求两个1必须在 水平或者竖直的四个方向上 相邻。你可以假设grid的四个边缘都被0(代表水)包围着。岛屿的面积是岛上值为
1的单元格的数目。计算并返回
grid中最大的岛屿面积。如果没有岛屿,则返回面积为0。
class Solution {
typedef pair<int,int> PII;
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int path;
int m,n;
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
queue<PII> qu;
m=grid.size();
n=grid[0].size();
int _max=0;
path=0;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(grid[i][j]==1)
{
path=1;
qu.push({i,j});
grid[i][j]=0;
while(!qu.empty())
{
auto [a,b]=qu.front();
qu.pop();
for(int k=0;k<4;k++)
{
int x=a+dx[k];
int y=b+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1)
{
qu.push({x,y});
grid[x][y]='0';
path++;
}
}
}
_max=max(_max,path);
}
}
}
return _max;
}
};最短路问题
就是指从入口到出口的借用路径的最短距离,需要注意的是入口和出口可以是位置和单词等各种东西。
迷宫中离入口最近的出口
已解答
中等
相关标签
相关企业
提示
给你一个
m x n的迷宫矩阵maze(下标从 0 开始),矩阵中有空格子(用'.'表示)和墙(用'+'表示)。同时给你迷宫的入口entrance,用entrance = [entrancerow, entrancecol]表示你一开始所在格子的行和列。每一步操作,你可以往 上,下,左 或者 右 移动一个格子。你不能进入墙所在的格子,你也不能离开迷宫。你的目标是找到离
entrance最近 的出口。出口 的含义是maze边界 上的 空格子。entrance格子 不算 出口。请你返回从
entrance到最近出口的最短路径的 步数 ,如果不存在这样的路径,请你返回-1
class Solution {
public:
typedef pair<int, int> PII;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {
queue<PII> qu;
int ret=1;
int m = maze.size();
int n = maze[0].size();
qu.push({entrance[0], entrance[1]});
maze[entrance[0]][entrance[1]]='0';
while (!qu.empty())
{
int count=qu.size();
while(count--)
{
auto [a, b] = qu.front();
qu.pop();
for (int k = 0; k < 4; k++)
{
int x = a + dx[k];
int y = b + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == '.')
{
if(x==m-1||x==0||y==n-1||y==0)
{
return ret;
}
qu.push({x, y});
maze[x][y] = '0';
}
}
}
ret++;
}
return -1;
}
};十四 多源BFS
从多个起点开始扩散的bfs。
矩阵
已解答
中等
相关标签
相关企业
给定一个由
0和1组成的矩阵mat,请输出一个大小相同的矩阵,其中每一个格子是mat中对应位置元素到最近的0的距离。两个相邻元素间的距离为
1。
class Solution {
public:
typedef pair<int,int> PII;
int n;
int m;
int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
m=mat.size();
n=mat[0].size();
vector<vector<int>>ret(m,vector<int>(n,-1));
queue<PII> q;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(mat[i][j]==0)
{
q.push({i,j});
ret[i][j]=0;
}
}
}
while(q.size())
{
auto [a,b]=q.front();
q.pop();
for(int k=0;k<4;k++)
{
int x=dx[k]+a;
int y=dy[k]+b;
if(x>=0&&x<m&&y>=0&&y<n&&mat[x][y]==1)
{
mat[x][y]=-1;
ret[x][y]=ret[a][b]+1;
q.push({x,y});
}
}
}
return ret;
}
};BFS解决拓扑排序
流程:创建邻接表(或者邻接矩阵)和入度表,建图,拓扑排序。

课程表
已解答
中等
相关标签
相关企业
提示
你这个学期必须选修
numCourses门课程,记为0到numCourses - 1。在选修某些课程之前需要一些先修课程。 先修课程按数组
prerequisites给出,其中prerequisites[i] = [ai, bi],表示如果要学习课程ai则 必须 先学习课程bi。
- 例如,先修课程对
[0, 1]表示:想要学习课程0,你需要先完成课程1。请你判断是否可能完成所有课程的学习?如果可以,返回
true;否则,返回false。
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
int n=numCourses;
//1.邻接表和入度
unordered_map<int,vector<int>> edges;
vector<int> in(numCourses,0);
//2.建图
for(auto &e:prerequisites)
{
int a=e[0];int b=e[1];//b->a
edges[b].push_back(a);
in[a]++;
}
//3.拓扑排序
//(1).将入度为零的节点入队列
queue<int> q;
for(int i=0;i<n;i++)
{
if(in[i]==0)
q.push(i);
}
//(2).bfs
while(q.size())
{
int t=q.front();
q.pop();
//a.删除边
for(auto e:edges[t])
{
in[e]--;
if(in[e]==0)
{
q.push(e);
}
}
}
for(auto &e:in)
{
if(e!=0)
return false;
}
return true;
}
};