一、CE Loss
定义
交叉熵损失(Cross-Entropy Loss,CE Loss)能够衡量同一个随机变量中的两个不同概率分布的差异程度,当两个概率分布越接近时,交叉熵损失越小,表示模型预测结果越准确。
公式
二分类
二分类的CE Loss公式如下,
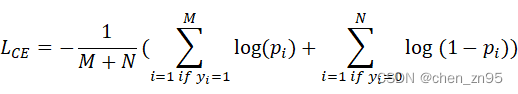
其中,:正样本数量,
:负样本数量,
:真实值,
:预测值
多分类
在计算多分类的CE Loss时,首先需要对模型输出结果进行softmax处理。公式如下,
![]()

其中, :模型输出,
:对模型输出进行softmax处理后的值,
![]() :真实值的one hot编码(假设模型在做5分类,如果
:真实值的one hot编码(假设模型在做5分类,如果=2,则
![]() =[0,0,1,0,0])
=[0,0,1,0,0])
代码实现
二分类
import torch
import torch.nn as nn
import math
criterion = nn.BCELoss()
output = torch.rand(1, requires_grad=True)
label = torch.randint(0, 1, (1,)).float()
loss = criterion(output, label)
print("预测值:", output)
print("真实值:", label)
print("nn.BCELoss:", loss)
for i in range(label.shape[0]):
if label[i] == 0:
res = -math.log(1-output[i])
elif label[i] == 1:
res = -math.log(output[i])
print("自己的计算结果", res)
"""
预测值: tensor([0.7359], requires_grad=True)
真实值: tensor([0.])
nn.BCELoss: tensor(1.3315, grad_fn=<BinaryCrossEntropyBackward0>)
自己的计算结果 1.331509556677378
"""多分类
import torch
import torch.nn as nn
import math
criterion = nn.CrossEntropyLoss()
output = torch.randn(1, 5, requires_grad=True)
label = torch.empty(1, dtype=torch.long).random_(5)
loss = criterion(output, label)
print("预测值:", output)
print("真实值:", label)
print("nn.CrossEntropyLoss:", loss)
output = torch.softmax(output, dim=1)
print("softmax后的预测值:", output)
one_hot = torch.zeros_like(output).scatter_(1, label.view(-1, 1), 1)
print("真实值对应的one_hot编码", one_hot)
res = (-torch.log(output) * one_hot).sum()
print("自己的计算结果", res)
"""
预测值: tensor([[-0.7459, -0.3963, -1.8046, 0.6815, 0.2965]], requires_grad=True)
真实值: tensor([1])
nn.CrossEntropyLoss: tensor(1.9296, grad_fn=<NllLossBackward0>)
softmax后的预测值: tensor([[0.1024, 0.1452, 0.0355, 0.4266, 0.2903]], grad_fn=<SoftmaxBackward0>)
真实值对应的one_hot编码 tensor([[0., 1., 0., 0., 0.]])
自己的计算结果 tensor(1.9296, grad_fn=<SumBackward0>)
"""二、Focal Loss
定义
虽然CE Loss能够衡量同一个随机变量中的两个不同概率分布的差异程度,但无法解决以下两个问题:1、正负样本数量不平衡的问题(如centernet的分类分支,它只将目标的中心点作为正样本,而把特征图上的其它像素点作为负样本,可想而知正负样本的数量差距之大);2、无法区分难易样本的问题(易分类的样本的分类错误的损失占了整体损失的绝大部分,并主导梯度)
为了解决以上问题,Focal Loss在CE Loss的基础上改进,引入了:1、正负样本数量调节因子以解决正负样本数量不平衡的问题;2、难易样本分类调节因子以聚焦难分类的样本
公式
二分类
公式如下,

![]()

其中,:正负样本数量调节因子,
:难易样本分类调节因子
多分类

其中,:
类别的权重
代码实现
二分类
def sigmoid_focal_loss(
inputs: torch.Tensor,
targets: torch.Tensor,
alpha: float = -1,
gamma: float = 2,
reduction: str = "none",
) -> torch.Tensor:
"""
Loss used in RetinaNet for dense detection: https://arxiv.org/abs/1708.02002.
Args:
inputs: A float tensor of arbitrary shape.
The predictions for each example.
targets: A float tensor with the same shape as inputs. Stores the binary
classification label for each element in inputs
(0 for the negative class and 1 for the positive class).
alpha: (optional) Weighting factor in range (0,1) to balance
positive vs negative examples. Default = -1 (no weighting).
gamma: Exponent of the modulating factor (1 - p_t) to
balance easy vs hard examples.
reduction: 'none' | 'mean' | 'sum'
'none': No reduction will be applied to the output.
'mean': The output will be averaged.
'sum': The output will be summed.
Returns:
Loss tensor with the reduction option applied.
"""
inputs = inputs.float()
targets = targets.float()
p = torch.sigmoid(inputs)
ce_loss = F.binary_cross_entropy_with_logits(inputs, targets, reduction="none")
p_t = p * targets + (1 - p) * (1 - targets)
loss = ce_loss * ((1 - p_t) ** gamma)
if alpha >= 0:
alpha_t = alpha * targets + (1 - alpha) * (1 - targets)
loss = alpha_t * loss
if reduction == "mean":
loss = loss.mean()
elif reduction == "sum":
loss = loss.sum()
return loss步骤1、首先对输入进行sigmoid处理,
p = torch.sigmoid(inputs)步骤2、随后求出CE Loss,
ce_loss = F.binary_cross_entropy_with_logits(inputs, targets, reduction="none")步骤3、定义,公式为:

p_t = p * targets + (1 - p) * (1 - targets)步骤4、为CE Loss添加难易样本分类调节因子,
loss = ce_loss * ((1 - p_t) ** gamma)步骤5、定义,公式为:
![]()
alpha_t = alpha * targets + (1 - alpha) * (1 - targets)步骤6、为步骤4的损失添加正负样本数量调节因子,
loss = alpha_t * loss多分类
def multi_cls_focal_loss(
inputs: torch.Tensor,
targets: torch.Tensor,
alpha: torch.Tensor,
gamma: float = 2,
reduction: str = "none",
) -> torch.Tensor:
inputs = inputs.float()
targets = targets.float()
ce_loss = nn.CrossEntropyLoss()(inputs, targets, reduction="none")
one_hot = torch.zeros_like(inputs).scatter_(1, targets.view(-1, 1), 1)
p_t = inputs * one_hot
loss = ce_loss * ((1 - p_t) ** gamma)
if alpha >= 0:
alpha_t = alpha * one_hot
loss = alpha_t * loss
return loss三、GHMC Loss
定义
Focal Loss在CE Loss的基础上改进后,解决了正负样本不平衡以及无法区分难易样本的问题,但也会过分关注难分类的样本(离群点),导致模型学歪。为了解决这个问题,GHMC(Gradient Harmonizing Mechanism-C)定义了梯度模长,该梯度模长正比于分类的难易程度,目的是让模型不要关注那些容易学的样本,也不要关注那些特别难分的样本
公式
1、定义梯度模长
二分类的CE Loss公式如下,

假设x是模型的输出,假设p=sigmoid(x),求损失对x的偏导,
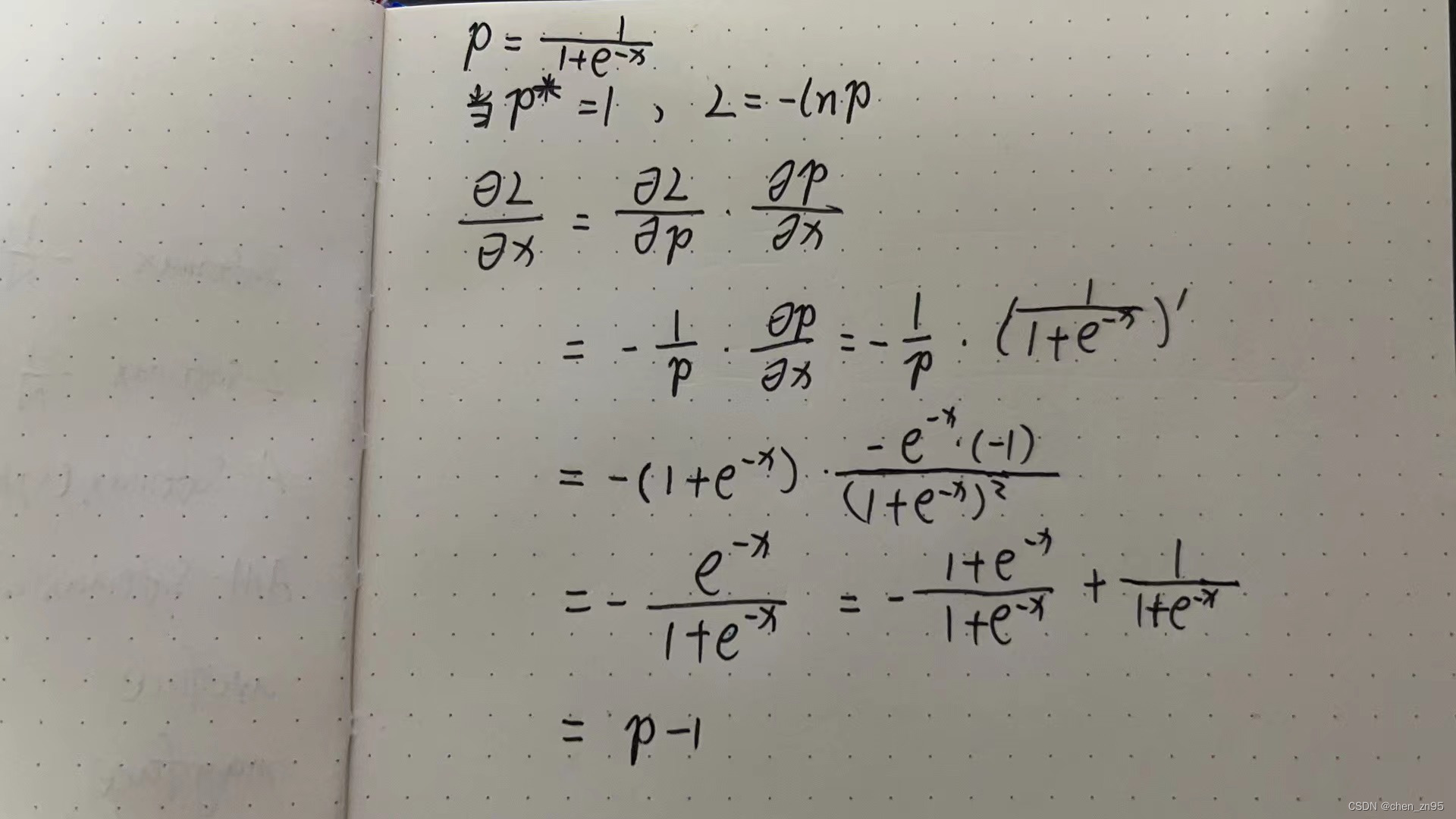

因此,定义梯度模长如下,

其中, :预测值,
:真实值
梯度模长与样本数量的关系如下,

2、定义梯度密度(单位梯度模长g上的样本数量)



其中,:第k个样本的梯度模长,
:
在
范围内的样本数量,
:区间
的长度
3、定义梯度密度协调参数(gradient density harmonizing parameter)

其中,:样本总数
4、定义GHMC Loss
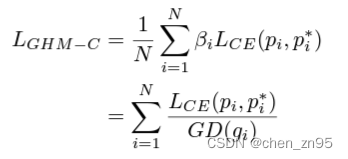
代码实现
def _expand_binary_labels(labels, label_weights, label_channels):
bin_labels = labels.new_full((labels.size(0), label_channels), 0)
inds = torch.nonzero(labels >= 1).squeeze()
if inds.numel() > 0:
bin_labels[inds, labels[inds] - 1] = 1
bin_label_weights = label_weights.view(-1, 1).expand(
label_weights.size(0), label_channels)
return bin_labels, bin_label_weights
class GHMC(nn.Module):
def __init__(
self,
bins=10,
momentum=0,
use_sigmoid=True,
loss_weight=1.0):
super(GHMC, self).__init__()
self.bins = bins
self.momentum = momentum
self.edges = [float(x) / bins for x in range(bins+1)]
self.edges[-1] += 1e-6
if momentum > 0:
self.acc_sum = [0.0 for _ in range(bins)]
self.use_sigmoid = use_sigmoid
self.loss_weight = loss_weight
def forward(self, pred, target, label_weight, *args, **kwargs):
""" Args:
pred [batch_num, class_num]:
The direct prediction of classification fc layer.
target [batch_num, class_num]:
Binary class target for each sample.
label_weight [batch_num, class_num]:
the value is 1 if the sample is valid and 0 if ignored.
"""
if not self.use_sigmoid:
raise NotImplementedError
# the target should be binary class label
if pred.dim() != target.dim():
target, label_weight = _expand_binary_labels(target, label_weight, pred.size(-1))
target, label_weight = target.float(), label_weight.float()
edges = self.edges
mmt = self.momentum
weights = torch.zeros_like(pred)
# 计算梯度模长
g = torch.abs(pred.sigmoid().detach() - target)
valid = label_weight > 0
tot = max(valid.float().sum().item(), 1.0)
# 设置有效区间个数
n = 0
for i in range(self.bins):
inds = (g >= edges[i]) & (g < edges[i+1]) & valid
num_in_bin = inds.sum().item()
if num_in_bin > 0:
if mmt > 0:
self.acc_sum[i] = mmt * self.acc_sum[i] \
+ (1 - mmt) * num_in_bin
weights[inds] = tot / self.acc_sum[i]
else:
weights[inds] = tot / num_in_bin
n += 1
if n > 0:
weights = weights / n
loss = F.binary_cross_entropy_with_logits(
pred, target, weights, reduction='sum') / tot
return loss * self.loss_weight步骤一、将梯度模长划分为bins(默认为10)个区域,
self.edges = [float(x) / bins for x in range(bins+1)]
"""
[0.0000, 0.1000, 0.2000, 0.3000, 0.4000, 0.5000, 0.6000, 0.7000, 0.8000, 0.9000, 1.0000]
"""步骤二、计算梯度模长
g = torch.abs(pred.sigmoid().detach() - target)步骤三、计算落入不同bin区间的梯度模长数量
valid = label_weight > 0
tot = max(valid.float().sum().item(), 1.0)
n = 0
for i in range(self.bins):
inds = (g >= edges[i]) & (g < edges[i+1]) & valid
num_in_bin = inds.sum().item()
if num_in_bin > 0:
if mmt > 0:
self.acc_sum[i] = mmt * self.acc_sum[i] + (1 - mmt) * num_in_bin
weights[inds] = tot / self.acc_sum[i]
else:
weights[inds] = tot / num_in_bin
n += 1
if n > 0:
weights = weights / n步骤四、计算GHMC Loss
loss = F.binary_cross_entropy_with_logits(pred, target, weights, reduction='sum') / tot * self.loss_weight
【参考文章】
Focal Loss的理解以及在多分类任务上的使用(Pytorch)_focal loss 多分类_GHZhao_GIS_RS的博客-CSDN博客
focal loss 通俗讲解 - 知乎
Focal Loss损失函数(超级详细的解读)_BigHao688的博客-CSDN博客
5分钟理解Focal Loss与GHM——解决样本不平衡利器 - 知乎