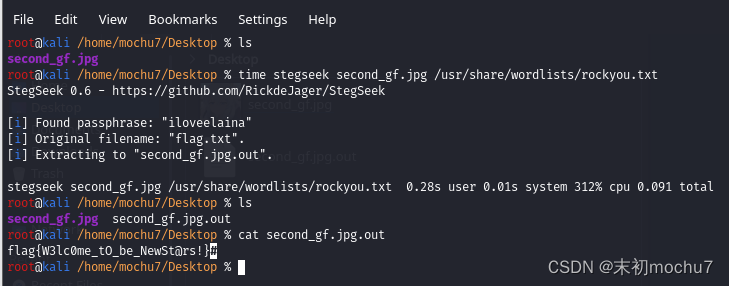
SVM 支持向量机
- SVM 原理
- 最优化问题
- 线性不可分
- sklearn 调用 SVM
- 核函数
SVM 原理
前置知识:用迭代策略来划分样本,请猛击《神经元的计算》。
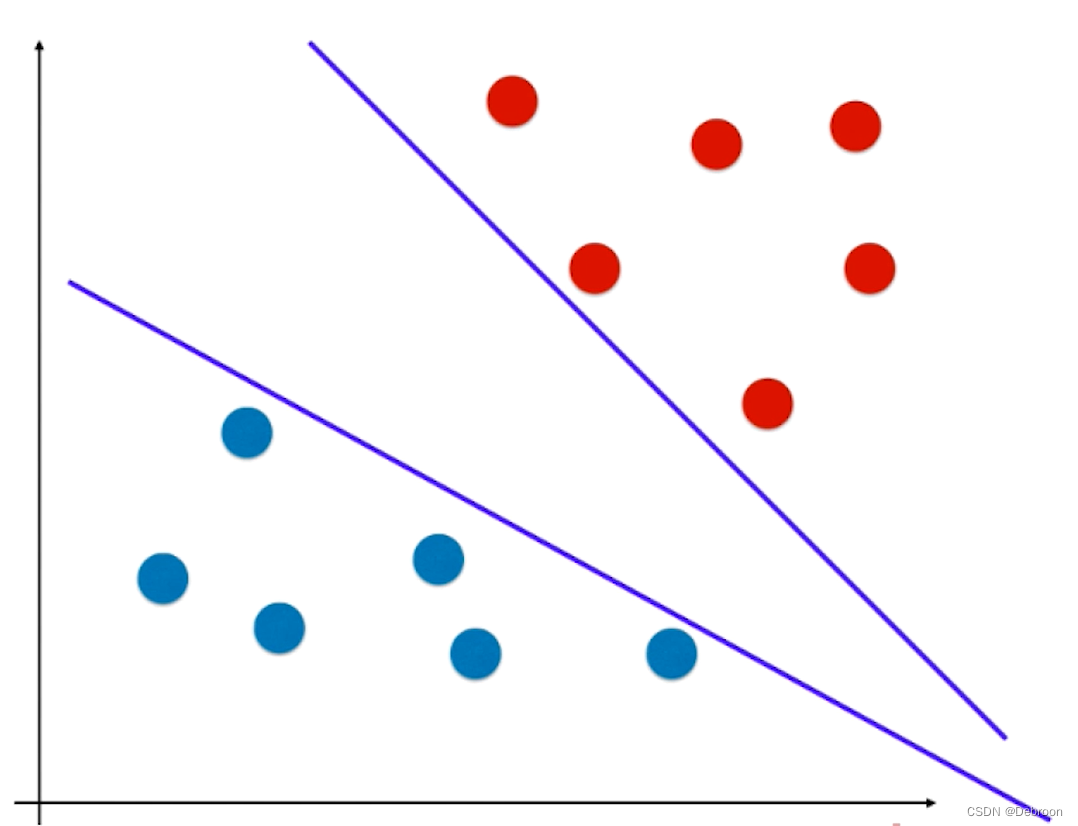
SVM 也是用一条迭代的直线来划分不同数据之间的边界:
.- 是一条直线(线性函数)
- 能将苹果和橘子分为两个部分(具有分类功能,是一种二值分类)
这样的线性函数,极端情况(直线逼近某一样本时),会把添加在附近的新样本误分在另外一侧,比如下图所示:
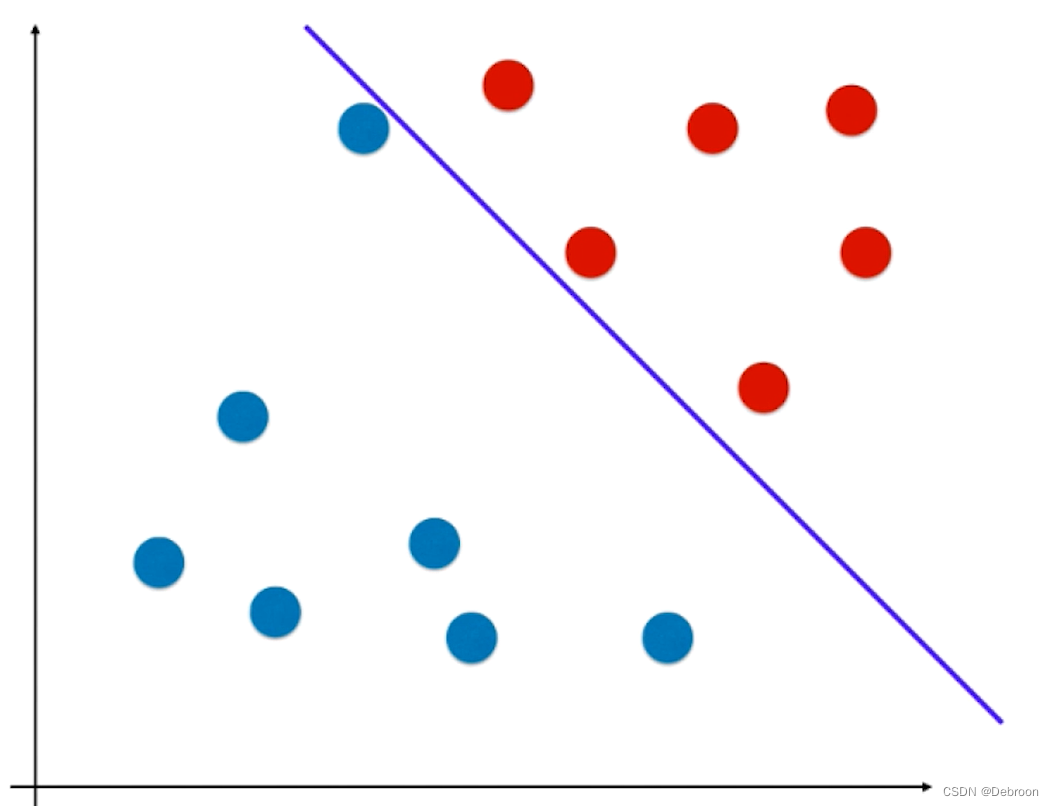
新添加的元素,按照距离来看,本应是属于红色样本。
结果因为直线过于逼近红色区域,导致被划分成蓝色样本了。
这个直线泛化能力不够好的问题,要么是在数据预处理部分做处理,要么是做正则化。
- 正则化的本质是一个概念,不同算法中的使用方式可能不同,但它们的目的都是一样的,都是在机器学习算法层面增加模型的泛化能力。
SVM 是在算法里面解决泛化问题,不同于线性函数的地方在于:
- 这条直线,一定位于苹果和橘子的正中间,尽可能的离俩个样本最远,如同男女课桌的军事分解线,处于正中间,不偏向任何一方(注重公平原则,才能保证双方利益最大化)。
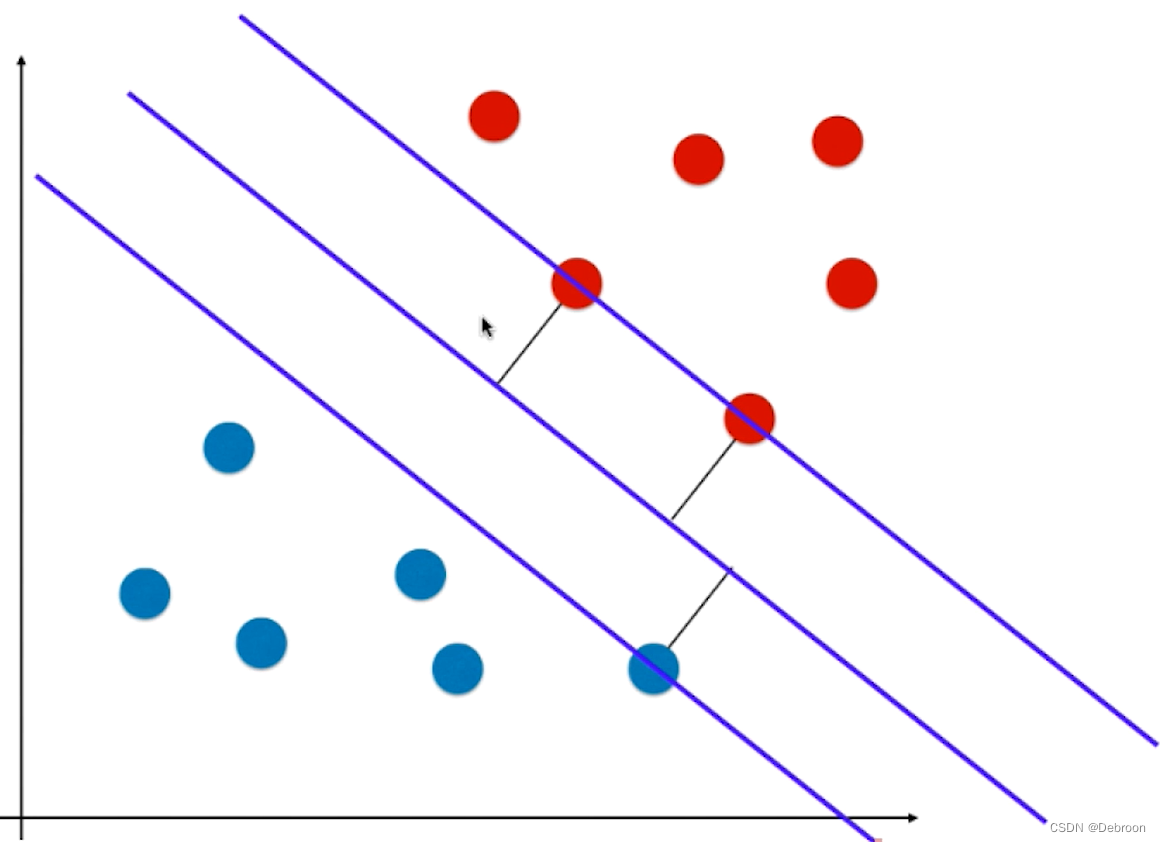
SVM 尝试寻找一条最优的决策边界,距离俩个类别最近的样本最远。
- 俩个类别最近的样本(被直线划中的蓝点、红点),叫支持向量,就是支持向量机 SVM 取名的由来
我们会用一个 margin 来描述这个距离:
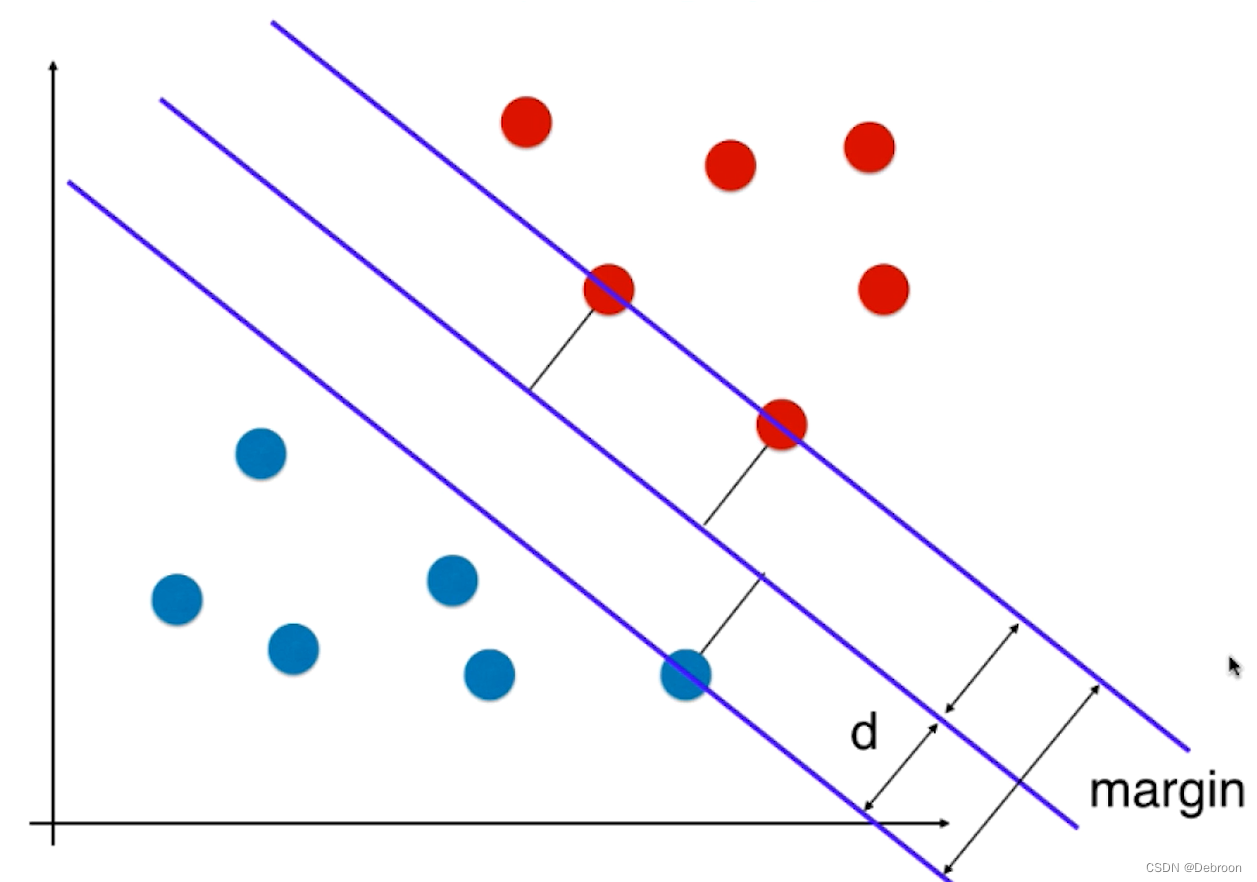
公平,就是要让 margin 最大化。
-
这种思维,也被称为 Hard Margin SVM,解决线性可分问题,找到一个决策边界,没有错误的将所有决策点进行划分。
-
但真实情况下,很多数据是线性不可分的,我们需要改进了 Hard Margin SVM,实现 Soft Margin SVM 解决线性不可分。
-
参数学习算法的固定套路:我们把算法思想(支持向量机的思想)转化为最优化问题、最优化目标函数。
最优化问题
因为 margin = 2d,margin 最大化也就是最大化 d。
还记得高中数学吗,点 (x, y) 到直线的距离公式:
- 点: ( x , y ) (x, y) (x,y)
- 直线方程: A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0
- 点 (x, y) 到直线 A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0 的距离公式: ∣ A x + B y + C ∣ A 2 + B 2 \frac{|Ax+By+C|}{\sqrt{A^{2}+B^{2}}} A2+B2∣Ax+By+C∣
这只是基于二维平面情况,我们再把这个公式,拓展到 N 维。
N 维点到直线的距离(推导过程不清楚可搜索一下):
- 点: [ x 1 , x 2 , x 3 , ⋅ ⋅ ⋅ , x n ] T = X [x_{1},x_{2},x_{3},···,x^{n}]^{T}=X [x1,x2,x3,⋅⋅⋅,xn]T=X,这里的点就是支持向量
- 直线方程: W T X + b = 0 , W T = [ w 1 , w 2 , w 3 , ⋅ ⋅ ⋅ , w n ] W^{T}X+b=0,W^{T}=[w_{1},w_{2},w_{3},···,w_{n}] WTX+b=0,WT=[w1,w2,w3,⋅⋅⋅,wn]
- 点到直线的距离公式: ∣ W T x + b ∣ ∣ ∣ w ∣ ∣ , ∣ ∣ w ∣ ∣ = w 1 2 + w 2 2 + w 3 2 + ⋅ ⋅ ⋅ + w n 2 \frac{|W^{T}x+b|}{||w||},||w||=\sqrt{w_{1}^{2}+w_{2}^{2}+w_{3}^{2}+···+w_{n}^{2}} ∣∣w∣∣∣WTx+b∣,∣∣w∣∣=w12+w22+w32+⋅⋅⋅+wn2
分子 ∣ A x + B y + C ∣ |Ax + By + C| ∣Ax+By+C∣ 就是 ∣ W T x + b ∣ |W^{T}x + b| ∣WTx+b∣,分母 ( A 2 + B 2 ) \sqrt(A^2 + B^2) (A2+B2) 就是 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣。
把这个公式代入 SVM 中:
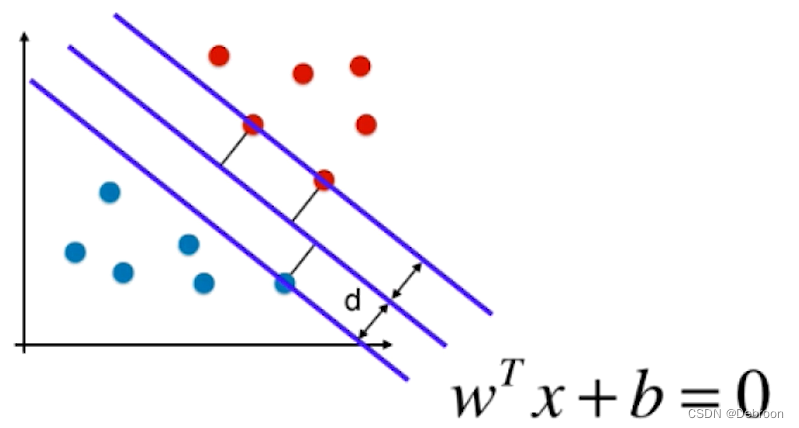
假设中间的直线方程是:
W
T
x
+
b
=
0
W^{T}x+b=0
WTx+b=0
那上下俩条直线就可以这样表示了:
- 上: W T x i + b ∣ ∣ w ∣ ∣ > = d , y i = 1 \frac{W^{T}x^{i}+b}{||w||}>=d,y^{i}=1 ∣∣w∣∣WTxi+b>=d,yi=1
- 下: W T x i + b ∣ ∣ w ∣ ∣ < = − d , y i = − 1 \frac{W^{T}x^{i}+b}{||w||}<=-d,y^{i}=-1 ∣∣w∣∣WTxi+b<=−d,yi=−1
格式俩边都除以 d:
- 上: W T x i + b ∣ ∣ w ∣ ∣ d > = 1 , y i = 1 \frac{W^{T}x^{i}+b}{||w||d}>=1,y^{i}=1 ∣∣w∣∣dWTxi+b>=1,yi=1
- 下: W T x i + b ∣ ∣ w ∣ ∣ d < = − 1 , y i = − 1 \frac{W^{T}x^{i}+b}{||w||d}<=-1,y^{i}=-1 ∣∣w∣∣dWTxi+b<=−1,yi=−1
因为 w 、 d w、d w、d 都是一个具体的数,我们可以约分。
分子、分母都除以 ∣ ∣ w ∣ ∣ d ||w||d ∣∣w∣∣d:
- 上: W d T x i + b d > = 1 , y i = 1 W^{T}_{d}x^{i}+b_{d}>=1,y^{i}=1 WdTxi+bd>=1,yi=1
- 下:
W
d
T
x
i
+
b
d
<
=
−
1
,
y
i
=
−
1
W^{T}_{d}x^{i}+b_{d}<=-1,y^{i}=-1
WdTxi+bd<=−1,yi=−1
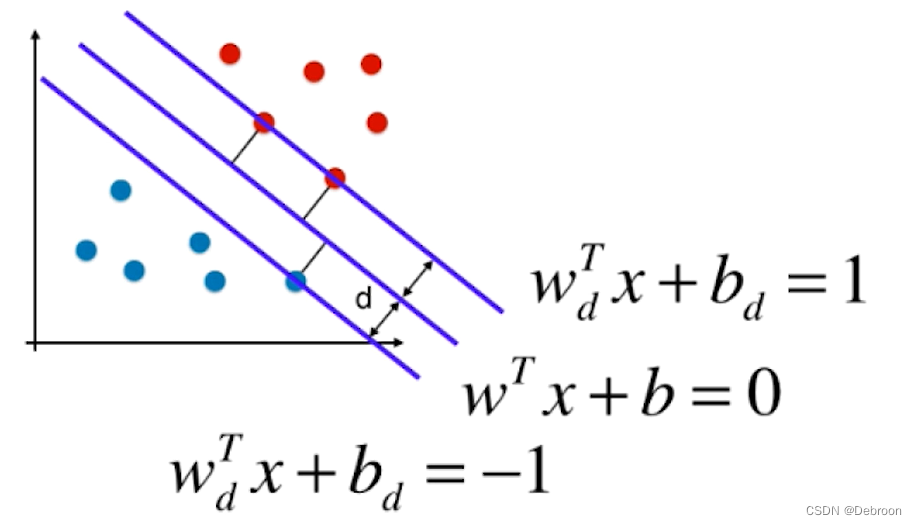
- 上: W d T x i + b d = 1 W^{T}_{d}x^{i}+b_{d}=1 WdTxi+bd=1
- 下: W d T x i + b d = − 1 W^{T}_{d}x^{i}+b_{d}=-1 WdTxi+bd=−1
我们把中间的直线,也除以 ∣ ∣ w ∣ ∣ d ||w||d ∣∣w∣∣d:
- 中: W d T x i + b d = 0 W^{T}_{d}x^{i}+b_{d}=0 WdTxi+bd=0
既然所有直线都是 W d T 、 b d W^{T}_{d}、b_{d} WdT、bd,那我们用 W T 、 b W^{T}、b WT、b 来简写。
将式子中的 W d 、 b d W_{d}、b_{d} Wd、bd 重新命名成了 W 、 d W、d W、d,实际还是 W d 、 b d W_{d}、b_{d} Wd、bd。
- 上: W T x i + b = 1 W^{T}x^{i}+b=1 WTxi+b=1
- 中: W T x i + b = 0 W^{T}x^{i}+b=0 WTxi+b=0
- 下: W T x i + b = − 1 W^{T}x^{i}+b=-1 WTxi+b=−1

【细节扩展】(可跳过)
.
我们为什么能够把 w d w_{d} wd 和 b d b_{d} bd 的那个 d d d 去掉,不是说去掉以后, w d = w w_{d}=w wd=w, b d = b b_{d}=b bd=b,而是,由于 d d d 是一个常数,所以,如果 d d d 不等于 1 1 1 的话,我们总能找到另外一组 w w w 和 b b b,和原假设是等价的,这组 w w w 和 b b b 就是 w d w_{d} wd 和 b d b_{d} bd。
.
或者说,虽然我们最初假设两条线是 w x + b = d wx+b =d wx+b=d 和 w x + b = − d wx+b=-d wx+b=−d,但我们总能找到另外一组 w w w 和 b b b,使得这两条同样的直线方程,改写成 w x + b = 1 wx+b=1 wx+b=1 和 w x + b = − 1 wx+b=-1 wx+b=−1 的形式。
.
我们后续推导,用这组让等式右侧等于 1 1 1 和 − 1 -1 −1 的 w w w 和 b b b !
.
用这组让等式右侧等于 1 1 1 和 − 1 -1 −1 的,并不会改变我们之前推导的 SVM 的优化的内容。所以,在这里,可以带进去。
话分俩头,我们再把上、下直线变成一个:
- 上: W T x i + b > = 1 , y i = 1 W^{T}x^{i}+b>=1,y^{i}=1 WTxi+b>=1,yi=1
- 下: W T x i + b < = − 1 , y i = − 1 W^{T}x^{i}+b<=-1,y^{i}=-1 WTxi+b<=−1,yi=−1
组合式子:
- 限定条件: y i ( W T x i + b ) > = 1 y^{i}(W^{T}x^{i}+b)>=1 yi(WTxi+b)>=1,所有数据点都必须在上、下直线之上或者之外
这个式子是限定条件,对于任意支持向量,都满足这个不等式关系。
我们现在就是在这个限定条件下,最优化这个问题。
回到开头提出的问题:
因为
margin = 2d,margin最大化也就是最大化d。
那么,d 是什么?
d:支持向量到决策边界的距离。
- SVM 不是求 d 的最大值,SVM 求的是:在 d 最大的情况下,w 是什么。
- w 是我们关注的一切,因为 SVM 的解,就是一条直线,我们要求的是这个直线方程,即 w。
- 让 d 最大是这条直线要满足的条件。
因为支持向量就是一个点,决策边界就是一条线,SVM 的公平划分思想,就变成了点到直线的距离。
- 支持向量: ( x , y ) (x,y) (x,y)
- 直线方程: w x + b = 0 wx+b = 0 wx+b=0
- 对于任意一个点 ( x , y ) (x,y) (x,y),到直线 w x + b = 0 wx+b = 0 wx+b=0 的距离公式: d = ∣ W T ∗ x + b ∣ ∣ ∣ w ∣ ∣ d=\frac{|W^{T}*x+b|}{||w||} d=∣∣w∣∣∣WT∗x+b∣。
最大化 d: m a x ∣ W T ∗ x + b ∣ ∣ ∣ w ∣ ∣ max\frac{|W^{T}*x+b|}{||w||} max∣∣w∣∣∣WT∗x+b∣
- 代入这个式子中的支持向量的结果,要么等于 1(红色),要么等于 -1(蓝色)
所以,最大化 d: m a x 1 ∣ ∣ w ∣ ∣ max\frac{1}{||w||} max∣∣w∣∣1
也就是,最小化模: m i n ∣ ∣ w ∣ ∣ min||w|| min∣∣w∣∣。
- 为了方便求导,我们会改成: m i n 1 2 ∣ ∣ w ∣ ∣ 2 min\frac{1}{2}||w||^{2} min21∣∣w∣∣2
综上所述,SVM 就变成了一个最优化问题:
- 限定条件: y i ( W T x i + b ) > = 1 y^{i}(W^{T}x^{i}+b)>=1 yi(WTxi+b)>=1,所有数据点都必须在上、下直线之上或者之外
- 最优化: m i n 1 2 ∣ ∣ w ∣ ∣ 2 min\frac{1}{2}||w||^{2} min21∣∣w∣∣2
SVM:在满足限定条件下,最优化。
- 和全局最优化问题不同,有条件的最优化问题计算难度很大,这个数学推导是最复杂了,超过本科数学范畴,我也不会······
线性不可分
可能会有极少个数据样本很偏,如下图:
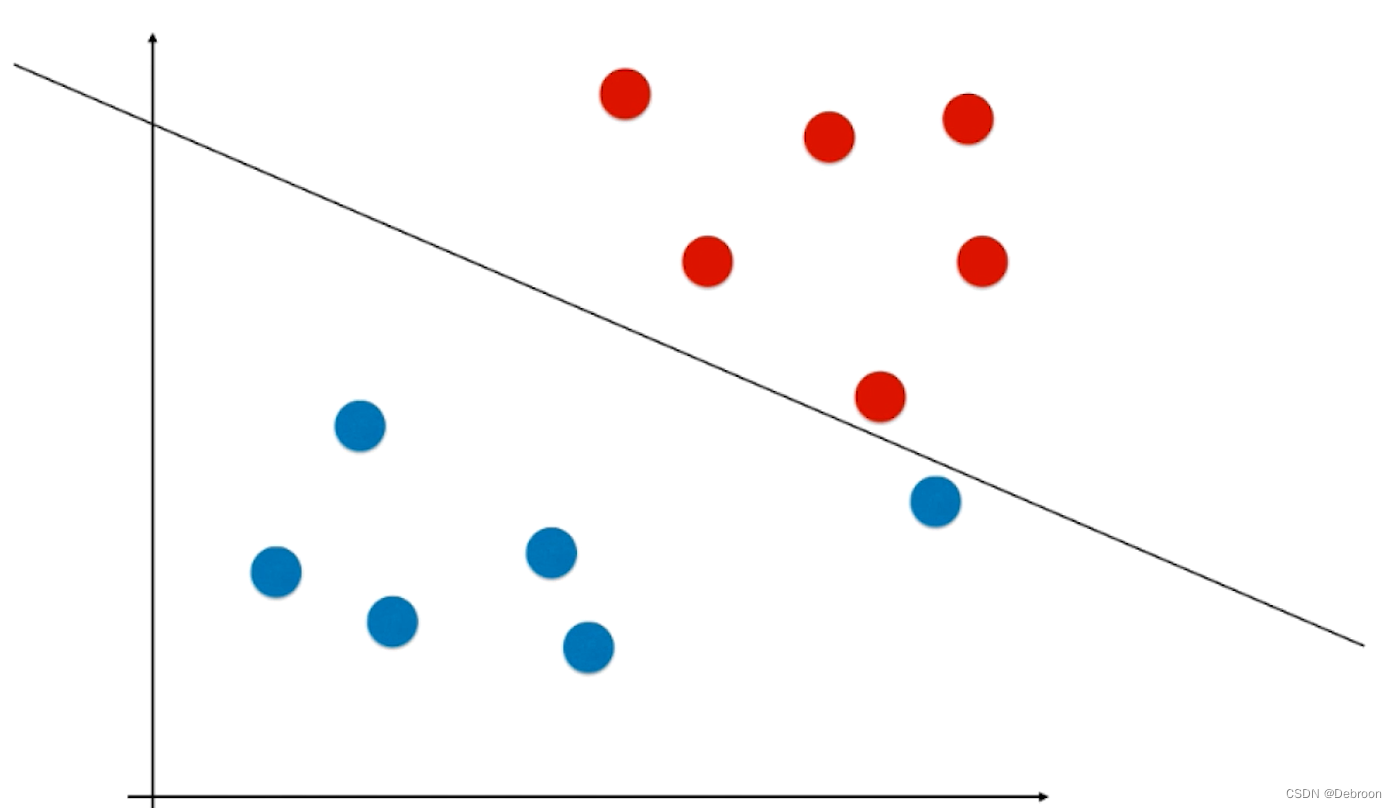
有一个蓝色节点远离其他蓝色节点,更靠近红色节点。
线性分类器为了分类正确,虽然正确的把俩种数据分开了,但泛化能力有点差,为了一个预测点过拟合了。
- 线性不可分:更极端的情况,这个蓝色节点出现在红色节点内部,那线性分类器会因为这样一个特殊点的存在,导致无法划分的情况。
在商业项目中,往往会有这种极端数据,如果不解决这种问题,就无法应用。
我们要追求泛化能力,我们希望有一定的容错能力,可以把一些点预测错误,提高泛化能力。
- 这种可以解决线性不可分的 SVM,也叫 Soft Margin SVM
SVM 是一个限定条件下的最优化问题:
- 限定条件: y i ( W T x i + b ) > = 1 y^{i}(W^{T}x^{i}+b)>=1 yi(WTxi+b)>=1
- 最优化: m i n 1 2 ∣ ∣ w ∣ ∣ 2 min\frac{1}{2}||w||^{2} min21∣∣w∣∣2
限定的条件是,所有数据点都必须在上、下直线之上或者之外。
我们宽松这个限定条件:让所有数据点不止在直线之上或者之外。
- 引入宽松
ζ
>
=
0
\zeta>=0
ζ>=0 后的限定条件:
y
i
(
W
T
x
i
+
b
)
>
=
1
−
ζ
i
y^{i}(W^{T}x^{i}+b)>=1-\zeta_{i}
yi(WTxi+b)>=1−ζi
- ζ i \zeta_{i} ζi 不是一个固定值,每个数据点都有一个 ζ i \zeta_{i} ζi。
- 为什么对于每一个样本来说,都有一个不同的 ζ i \zeta_{i} ζi,简单来说,是因为不是所有的错误都是相等的。
- 这个 ζ i \zeta_{i} ζi 不是超参数,而是模型参数,所以不需要我们设置。他就像线性回归中的 theta 一样,是在 fit 的过程中根据数据求出来的。
- ζ > = 0 \zeta>=0 ζ>=0 才会宽松,反之更严格。
宽松后的限定条件,在图上是一条虚线:
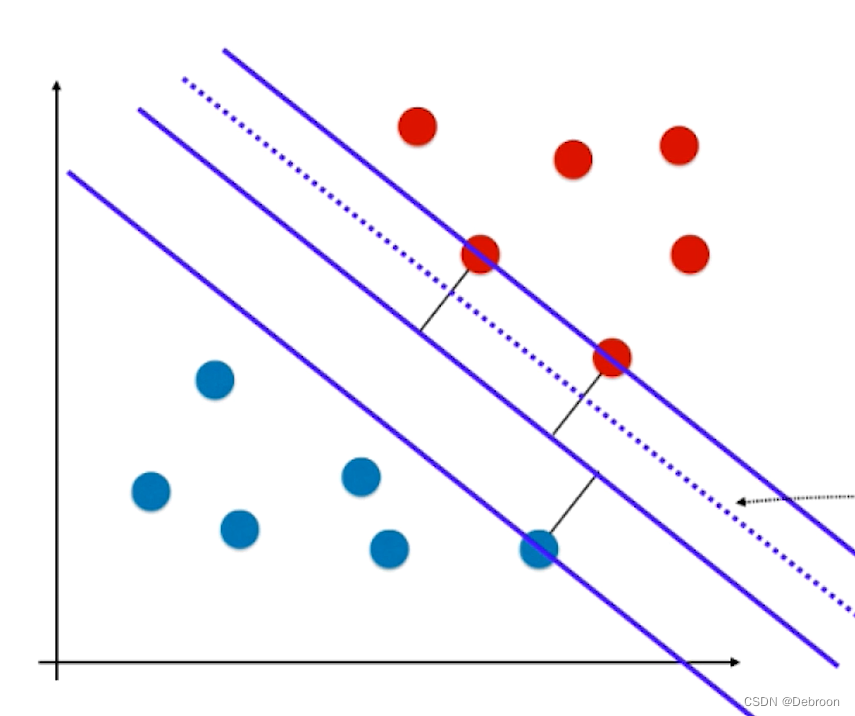
宽松后,允许数据点:
- 在上直线和上虚线之间
- 在下直线和下虚线之间
当然,仅仅设置 ζ > = 0 \zeta>=0 ζ>=0 是不够的。
- ζ = + ∞ \zeta=+∞ ζ=+∞ 时,上虚线会在上直线,下面无限远的地方,那红色方所有数据都可以满足了,太松
那怎么设置限定容错空间呢?加上 ∑ i = 1 m ζ i \sum^{m}_{i=1}\zeta_{i} ∑i=1mζi。
- 最优化: m i n 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m ζ i min\frac{1}{2}||w||^{2}+\sum^{m}_{i=1}\zeta_{i} min21∣∣w∣∣2+∑i=1mζi
这俩者之间也需要设置比例关系,添加一个变量 C:
- 最优化: m i n 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ζ i min\frac{1}{2}||w||^{2}+C\sum^{m}_{i=1}\zeta_{i} min21∣∣w∣∣2+C∑i=1mζi
如果 C 数值小,最优化公式大部分都在前面部分。
如果 C 数值大,最优化公式大部分都在后面部分。
宽松后的 SVM:
-
限定条件: y i ( W T x i + b ) > = 1 − ζ i y^{i}(W^{T}x^{i}+b)>=1-\zeta_{i} yi(WTxi+b)>=1−ζi
-
最优化: m i n 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ζ i min\frac{1}{2}||w||^{2}+C\sum^{m}_{i=1}\zeta_{i} min21∣∣w∣∣2+C∑i=1mζi
【拓展】
Hard SVM:每个数据点都在决策边界的一侧,且 margin 内没有数据点。
Soft SVM,数据点没有这个限制,但对于错误分类的数据点,或者 margin 内的数据点,很显然离正确的那个 margin 边界越近越好,也就是错误越小。
- ζ i \zeta_{i} ζi 在衡量每个数据点的这个错误。
- 我们的正则化项是看所有数据点的这个错误总和(或者平方和),來最小化ta。
sklearn 调用 SVM
from sklearn import datasets
from sklearn import model_selection
from sklearn import svm
# 加载数据集,sklearn提供的乳腺癌数据集load-barest-cancer(),这是一个简单经典的用于二分类任务的数据集。该数据集有539个样本,每个样本有30个特征。
cancer = datasets.load_breast_cancer()
X = cancer.data # 样本
y = cancer.target # 类别
# 将数据集进行划分,分成训练集和测试集
X_trainer, X_test, Y_trainer, Y_test = model_selection.train_test_split(X, y, test_size=0.2)
# 分类器
clf = svm.SVC(kernel="linear") # 调用 SVM,参数kernel为线性核函数
clf.fit(X_trainer, Y_trainer) # 训练分类器
print("Support Vector:\n", clf.n_support_) # 每一类中属于支持向量的点数目
print("Predict:\n", clf.predict(X_test)) # 对测试集的预测结果
score = clf.score(X_test, Y_test) # 模型得分
print("Score:", score)
输出:
Support Vector:
[25 26]
Predict:
[1 0 1 1 1 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 1 0 0 1 0 1
0 0 0 1 1 1 0 1 1 0 1 1 1 1 1 0 0 1 1 0 1 0 1 1 1 1 1 1 1 0 1 0 1 1 0 1 0
1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 0 1 1 1 0 0 0 1 0 1 1 1 1 0 0 1 0 1 1 1 1
0 1 1]
Score: 0.956140350877193(咋样,我是不是炒鸡棒(๑•̀ㅂ•́)و✧)