机器学习与深度学习——利用随机梯度下降算法SGD对波士顿房价数据进行线性回归

news2024/11/17 20:36:14

机器学习与深度学习——利用随机梯度下降算法SGD对波士顿房价数据进行线性回归

我们这次使用随机梯度下降（SGD）算法对波士顿房价数据进行线性回归的训练，给出每次迭代的权重、损失和梯度，并且绘制损失loss随着epoch变化的曲线图。

步骤

1、导入必要的库和模块：numpy，pandas，matplotlib，load_boston和StandardScaler。其中，load_boston用于加载波士顿房价数据集，StandardScaler用于对数据进行标准化处理。
2、加载数据集并对数据进行标准化处理。同时，为数据添加一列1作为截距项，并将y转换为列向量。
3、定义SGD函数来进行训练。在每个epoch中，我们会随机地从样本中抽取一个batch的数据来计算梯度和损失，并更新权重。
4、使用SGD训练模型，并输出每次迭代的结果：权重w，损失loss和梯度grad。同时，将每个epoch的平均损失存储到列表losses中，并返回最终的权重和损失。
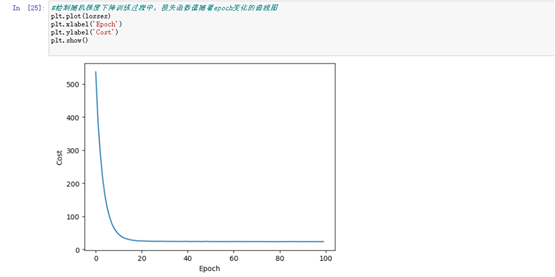
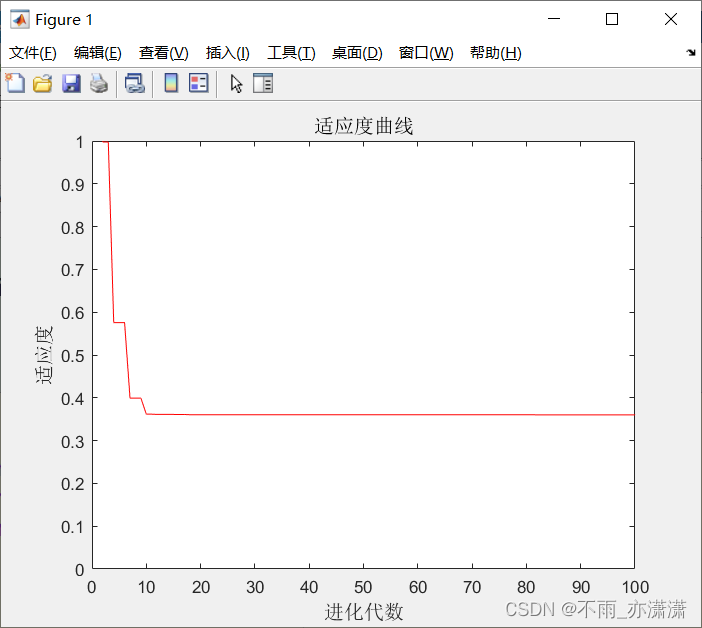
5、绘制随机梯度下降训练过程中，损失函数值随着epoch变化的曲线图

程序代码

1.使用随机梯度下降（SGD）算法对波士顿房价数据进行线性回归的训练，给出每次迭代的权重、损失和梯度，并且绘制了损失loss随着epoch变化的曲线图。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
#加载数据集并对数据进行标准化处理。同时，为数据添加一列1作为截距项，并将y转换为列向量。
# 加载数据
boston = load_boston()
X, y = boston.data, boston.target

# 标准化数据
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 在数据中添加一列1
X = np.hstack((np.ones((X.shape[0], 1)), X))

# 将y转换为列向量
y = y.reshape(-1, 1)
# 3、定义SGD函数来进行训练。在每个epoch中，我们会随机地从样本中抽取一个batch的数据来计算梯度和损失，并更新权重。
def sgd(X, y, lr=0.01, epochs=100, batch_size=32):
    n_samples, n_features = X.shape
    w = np.zeros((n_features, 1))
    losses = []
    
    for epoch in range(epochs):
        epoch_loss = 0
 
        # 随机排列样本
        permutation = np.random.permutation(n_samples)
        
        for i in range(0, n_samples, batch_size):
            # 获取一个batch的样本
            indices = permutation[i:i+batch_size]
            X_batch = X[indices]
            y_batch = y[indices]
            
            # 计算梯度和损失
            grad = X_batch.T.dot(X_batch.dot(w) - y_batch) / batch_size
            loss = np.mean((X_batch.dot(w) - y_batch) ** 2)
            epoch_loss += loss
            
            # 更新权重
            w -= lr * grad
        
        losses.append(epoch_loss / (n_samples // batch_size))
        
    return w, losses
# 使用SGD训练模型，并输出每次迭代的结果：权重w，损失loss和梯度grad。同时，将每个epoch的平均损失存储到列表losses中，并返回最终的权重和损失。
w, losses = sgd(X, y, lr=0.01, epochs=100, batch_size=32)

def sgd(X, y, lr=0.01, epochs=100, batch_size=32):
    n_samples, n_features = X.shape
    w = np.zeros((n_features, 1))
    losses = []
    
    for epoch in range(epochs):
        epoch_loss = 0
        
        # 随机排列样本
        permutation = np.random.permutation(n_samples)
        
        for i in range(0, n_samples, batch_size):
            # 获取一个batch的样本
            indices = permutation[i:i+batch_size]
            X_batch = X[indices]
            y_batch = y[indices]
            
            # 计算梯度和损失
            grad = X_batch.T.dot(X_batch.dot(w) - y_batch) / batch_size
            loss = np.mean((X_batch.dot(w) - y_batch) ** 2)
            epoch_loss += loss
            
            # 更新权重
            w -= lr * grad
            
            # 输出w值和grad值和loss值
            print('w:', w.flatten())
            print('grad:', grad.flatten())
            print('loss:', loss)
        
        losses.append(epoch_loss / (n_samples // batch_size))
        
    return w, losses

w, losses = sgd(X, y, lr=0.01, epochs=100, batch_size=32)



#绘制随机梯度下降训练过程中，损失函数值随着epoch变化的曲线图
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Cost')
plt.show()