方法1：通过动态规划解题，这道题也是动态规划的一道很好的入门题，因为比较简单和容易理解。

代码如下：

public int tribonacci(int n) {
        //处理特殊情况
        if(n==0){
            return 0;
        }
        if(n==1||n==2){
            return 1;
        }
        //定义数组
        int[]dp=new int[n+1];
        //初始化
        dp[0]=0;
        dp[1]=dp[2]=1;

        for(int i=3;i<=n;i++){
            dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
        }
        return dp[n];
    }

        动态规划的解题步骤分为5步

                1.状态表示

                2.状态转移方程

                3.初始化

                4.填表顺序

                5.返回值

        我们一开始的时候要根据题意以及经验判断需要用什么规格的dp表来表示数据的状态，由本题的思路我们可以创建一个一维数组的dp表，初始化一维数组的dp[0] dp[1]和dp[2]。

        根据题目已经给出的状态转移方程 dp[i]=dp[i-1]+dp[i-2]+dp[i-3] ，我们就以从左到右的顺序依次填满一维数组dp表，而填到dp[n]便得到了最终的答案

        方法2：对方法1的内存优化

代码如下：

public int tribonacci(int n){
        //处理特殊情况
        if(n==0){
            return 0;
        }
        if(n==1||n==2){
            return 1;
        }

        //定义变量，实现滚动数组
        int a=0,b=1,c=1,d=0;
        for(int i=3;i<=n;i++){
            d=a+b+c;
            a=b;
            b=c;
            c=d;
        }

        return d;
    }

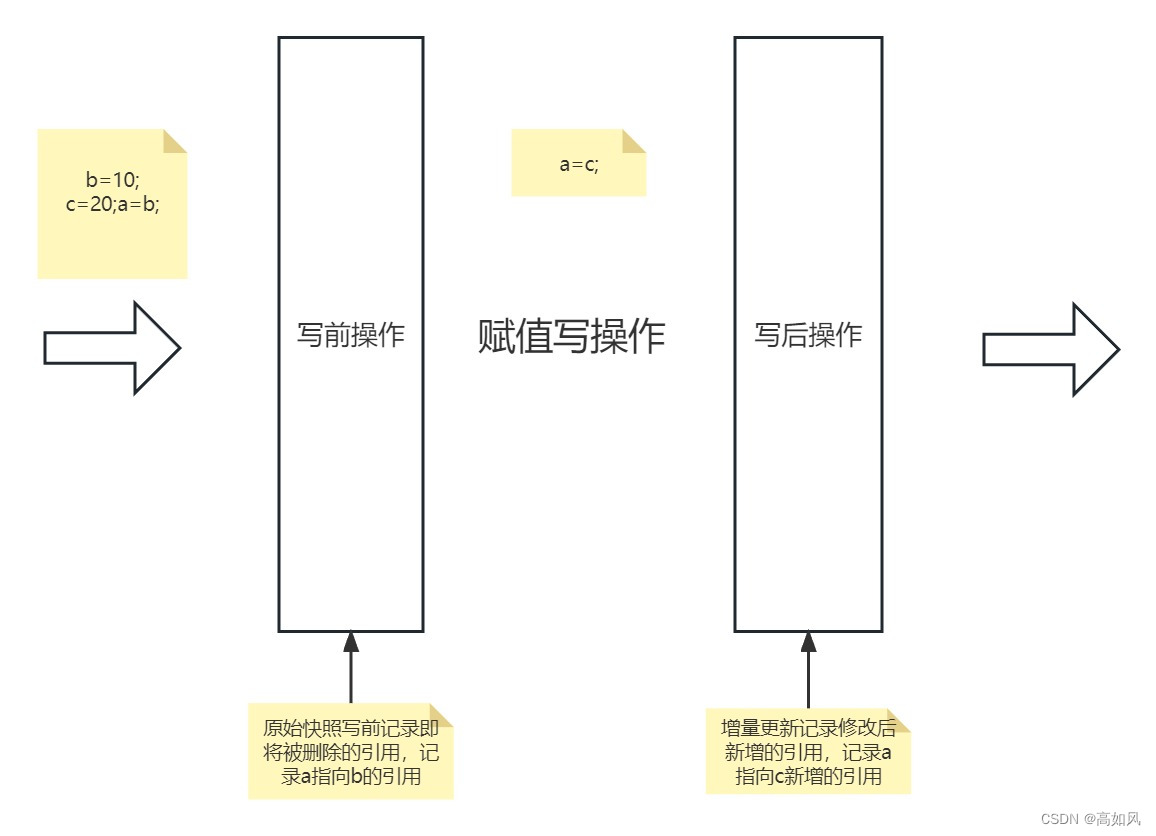
        根据状态转移方程，要求dp[n]的值只需要前面3个数据的值即可，所以我们一共只需要4个变量便可以实现滚动数组，用a,b,c三个变量表示已知的三个值，用d来接受a+b+c的值，后面再依次更新a，b，c的值，便可以依次获取到后面的值